CATEGORICAL LOGIC CATEGORIES Categorical logic concerns how we

CATEGORICAL LOGIC

CATEGORIES • Categorical logic concerns how we categorize things and their relationships. • Categories are groups of things. • We can arbitrarily categorize anything. – Tables, pizzas, tools, televisions, animals, blond people…

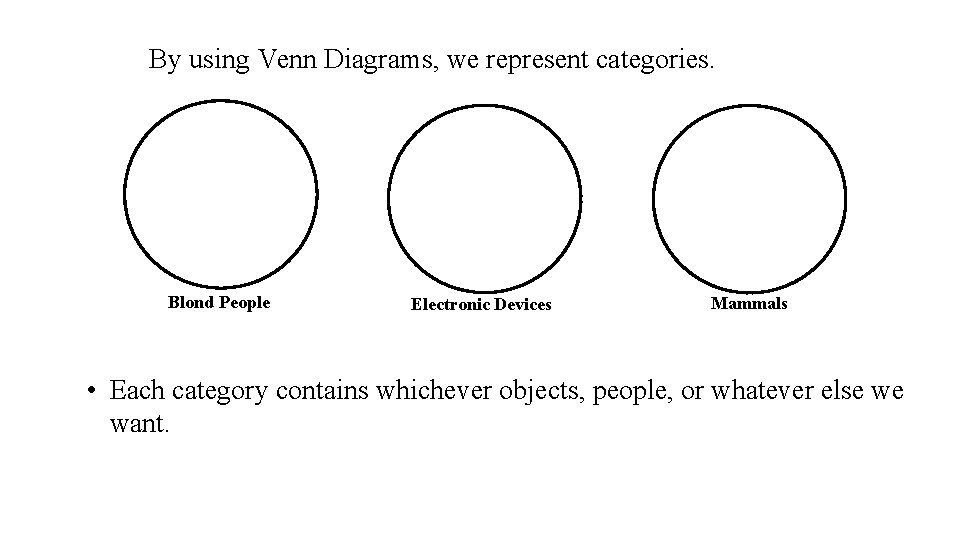
By using Venn Diagrams, we represent categories. Blond People Electronic Devices Mammals • Each category contains whichever objects, people, or whatever else we want.

• By using an X or by shading the area of a circle, I indicate various things: • By placing an X inside a category, I indicate that some members of that category exist. • X = at least 1. X Blond People • X means there exists at least 1 thing in the category, and it is a blond person.

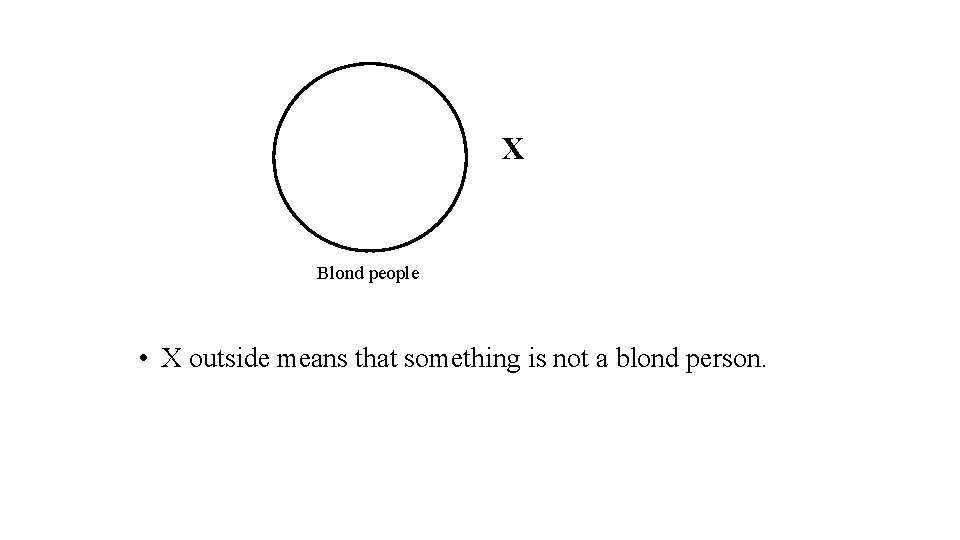
X Blond people • X outside means that something is not a blond person.

Blond people Shading completely the area mean there aren’t any blond people.

Blond people Shading outside means that everything is blond people.

• The objects, people, animals, etc. designated by a category may have logical relations with other categories. • For example I can say that all blond people are humans. • There are only 4 possibilities to indicate how the Subject relate to the Predicate.

• 1: All members contained in the category of the Subjects are members of the category of the Predicate: A-Form. • 2: No members contained in the category of the Subjects are members of the category of the Predicate: E-Form. • 3: Some members contained in the category of the Subjects are members of the category of the Predicate: I-Form. • 4: Some members contained in the category of the Subjects are not members of the category of the Predicate: O-Form.

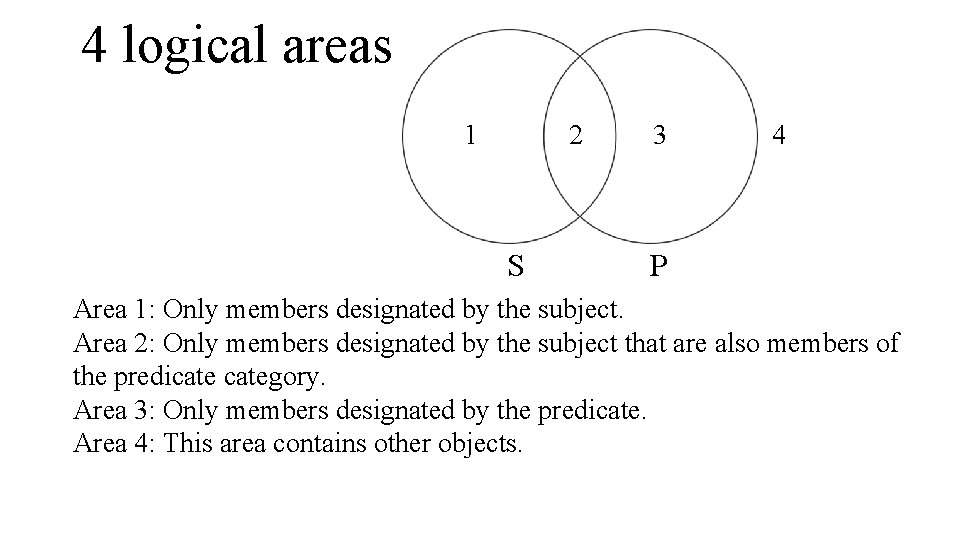
4 logical areas 1 2 S 3 4 P Area 1: Only members designated by the subject. Area 2: Only members designated by the subject that are also members of the predicategory. Area 3: Only members designated by the predicate. Area 4: This area contains other objects.

USING VENN DIAGRAMS TO REPRESENT THE 4 CATEGORICAL FORMS

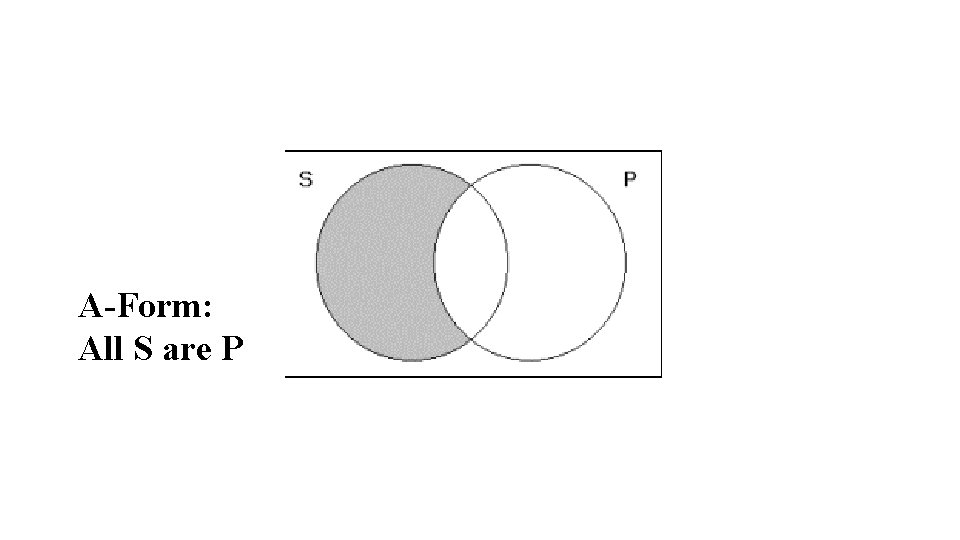
A-Form: All S are P

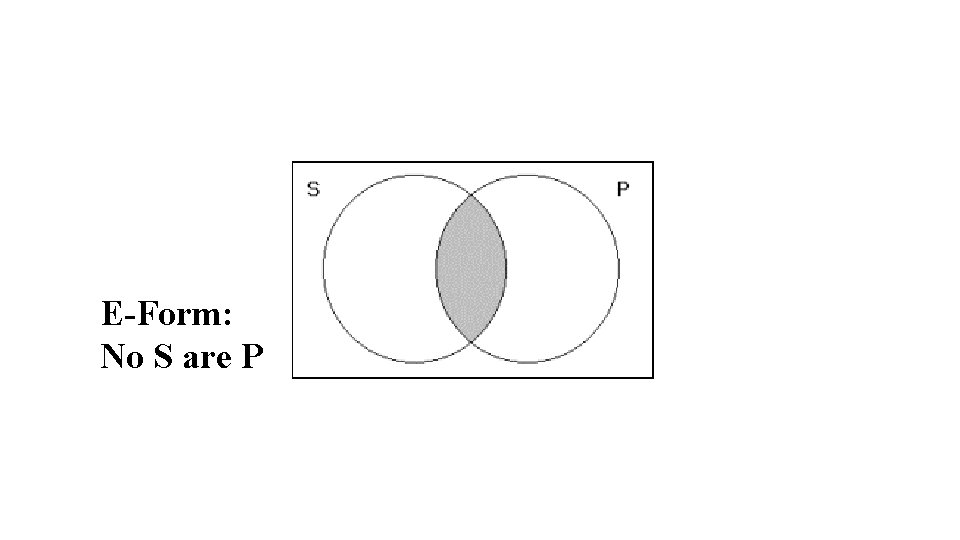
E-Form: No S are P

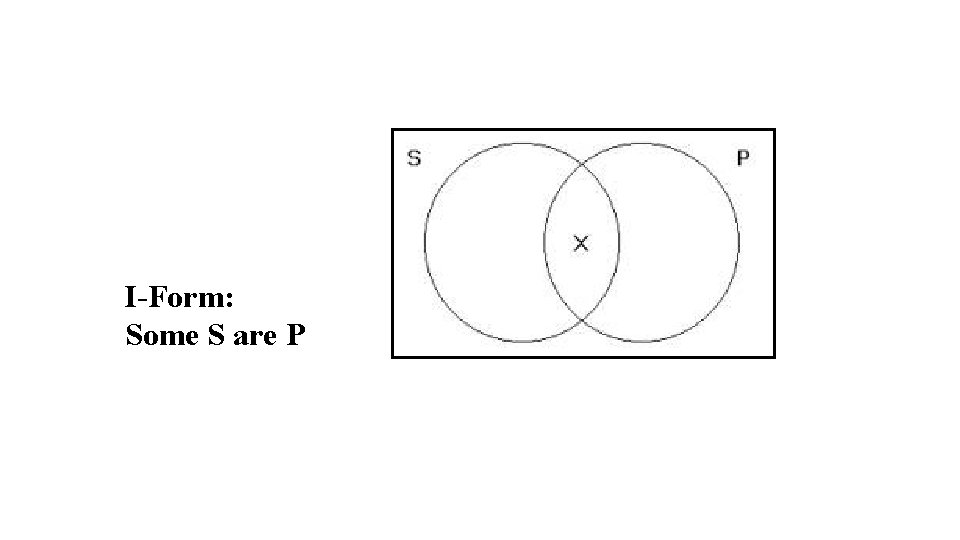
I-Form: Some S are P

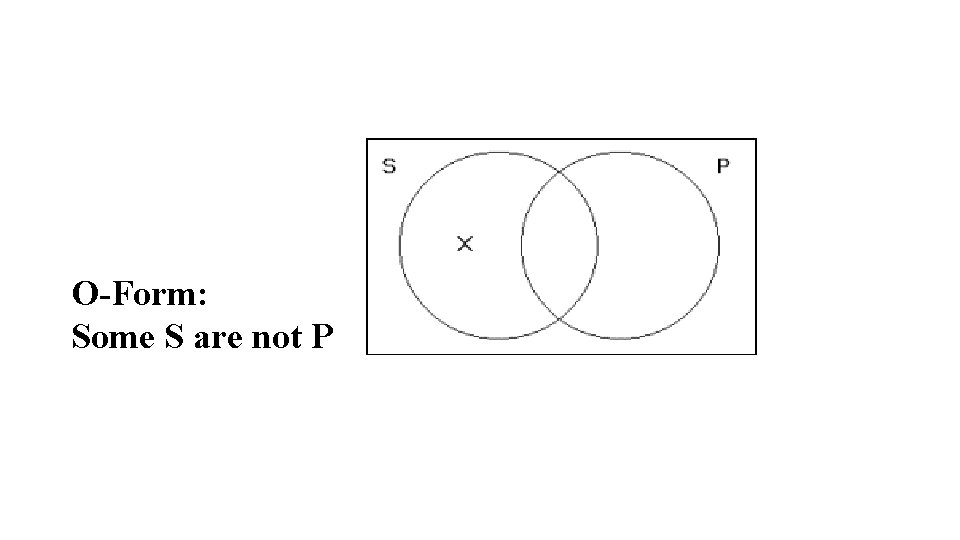
O-Form: Some S are not P

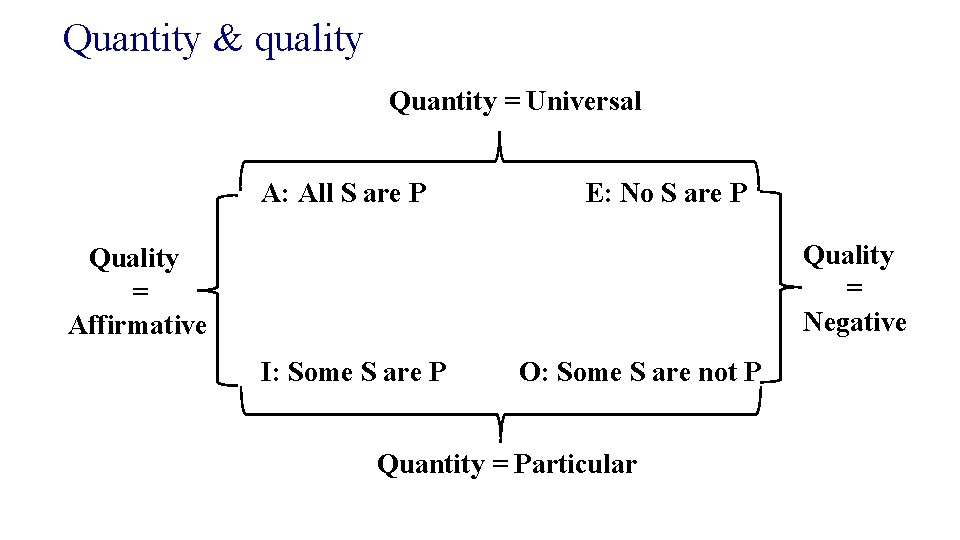
Quantity & quality Quantity = Universal A: All S are P E: No S are P Quality = Negative Quality = Affirmative I: Some S are P O: Some S are not P Quantity = Particular

DISTRIBUTION

• A proposition may refer to classes in different ways: to all members or some members. • The proposition “All senators are citizens” refers to all senators, but not to all citizens: All senators are citizens, but not all citizens are senators! • Distribution is concerned with to how many members of a class are referred to.

A term is distributed when it is used to refer to all member of a class. A term is undistributed when it is not used to refer to all members.

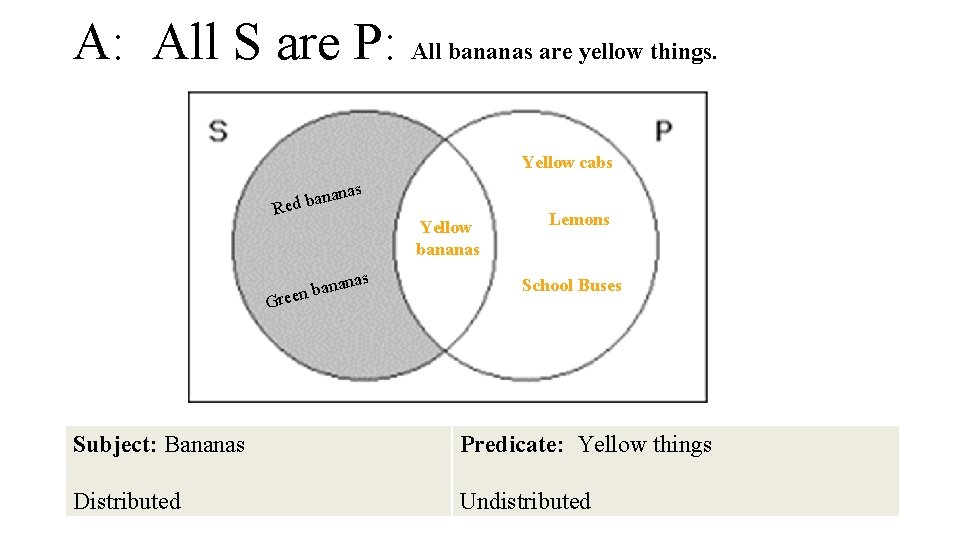
A: All S are P: All bananas are yellow things. Yellow cabs as nan a b d Re nana a b n e Gre Yellow bananas s Lemons School Buses Subject: Bananas Predicate: Yellow things Distributed Undistributed

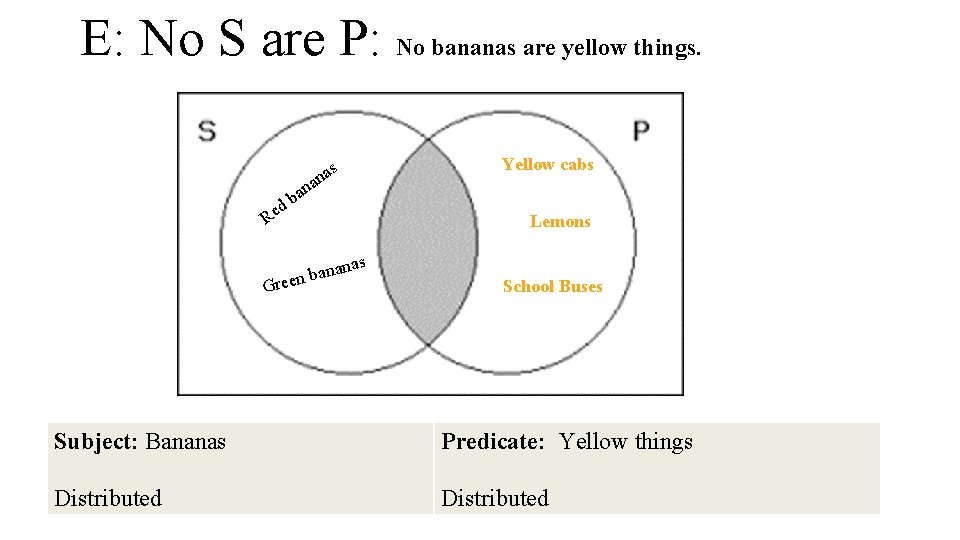
E: No S are P: No bananas are yellow things. d Re n ba s na a anas n a b reen G Yellow cabs Lemons School Buses Subject: Bananas Predicate: Yellow things Distributed

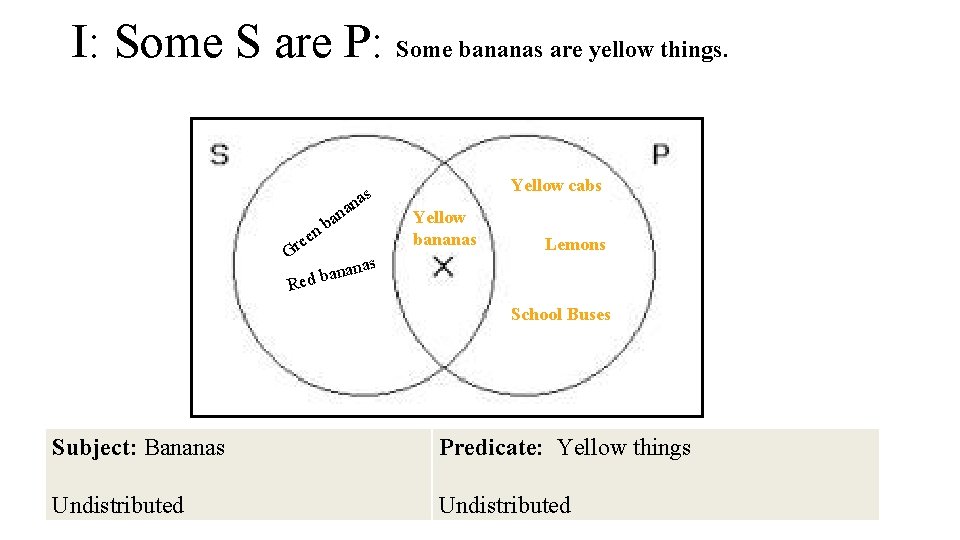
I: Some S are P: Some bananas are yellow things. nb ee r G a an as n anas n a b Red Yellow cabs Yellow bananas Lemons School Buses Subject: Bananas Predicate: Yellow things Undistributed

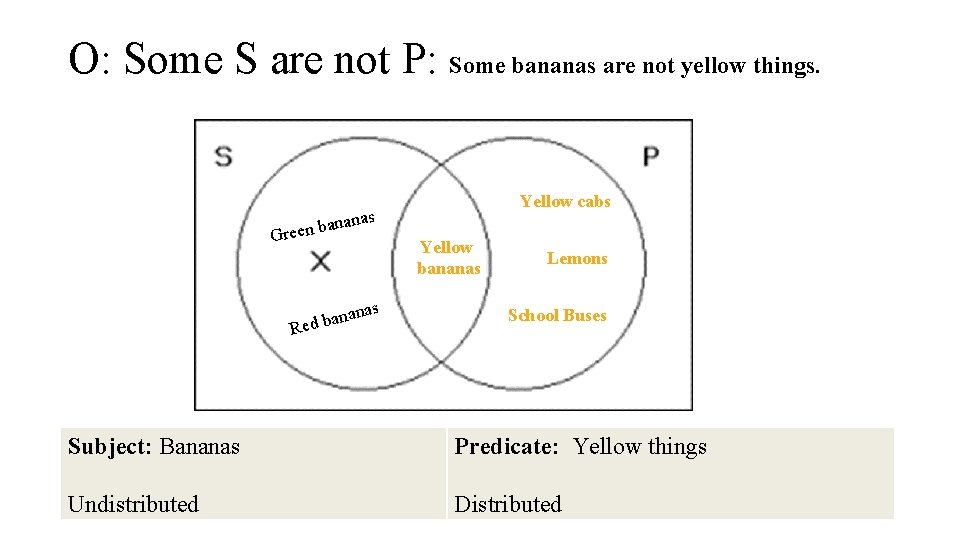
O: Some S are not P: Some bananas are not yellow things. Yellow cabs nas bana n e e r G anas n a b Red Yellow bananas Lemons School Buses Subject: Bananas Predicate: Yellow things Undistributed Distributed

OPPOSITION

OPPOSITIONS • OPPOSITION is the logical relation between any two categorical propositions. • Categorical propositions relate in 5 different ways:

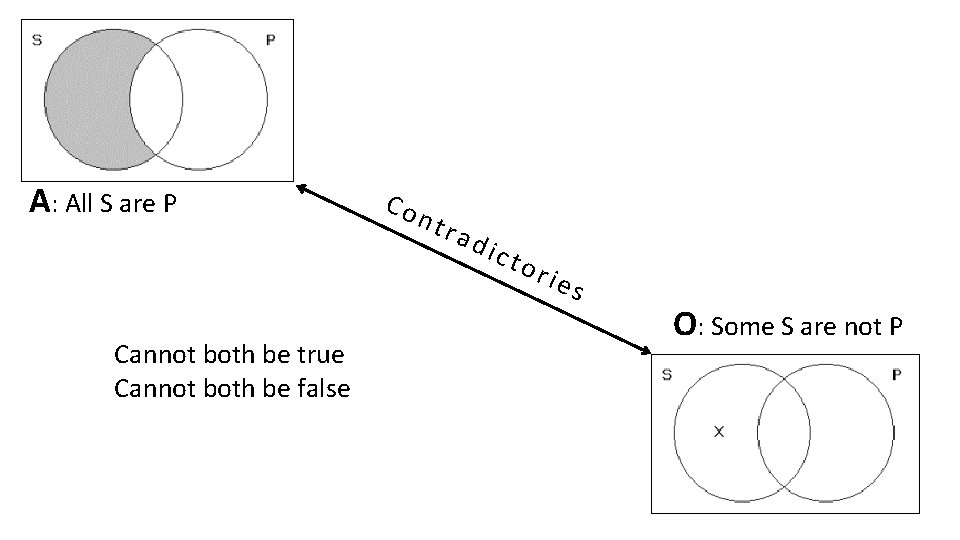
1. Contradictories Cannot both be true Cannot both be false

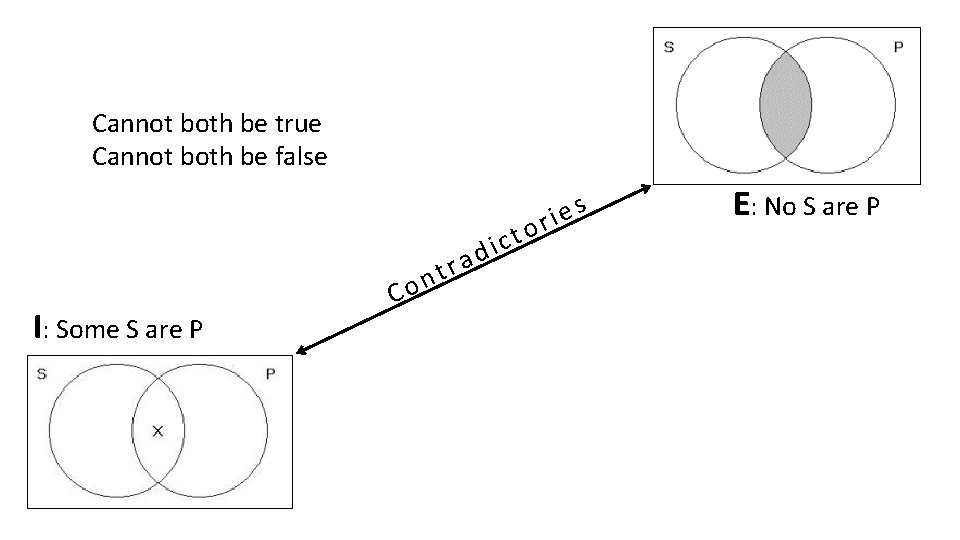
A: All S are P Cannot both be true Cannot both be false Co ntr ad ict ori es O: Some S are not P

Cannot both be true Cannot both be false I: Some S are P Co a r t n t c i d s e i or E: No S are P

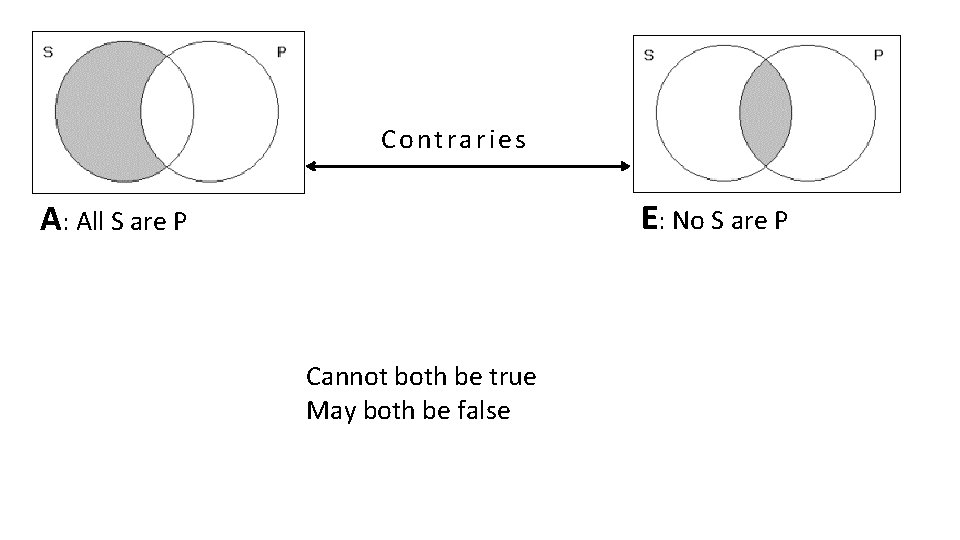
2. Contraries Cannot both be true May both be false

Contraries E: No S are P A: All S are P Cannot both be true May both be false

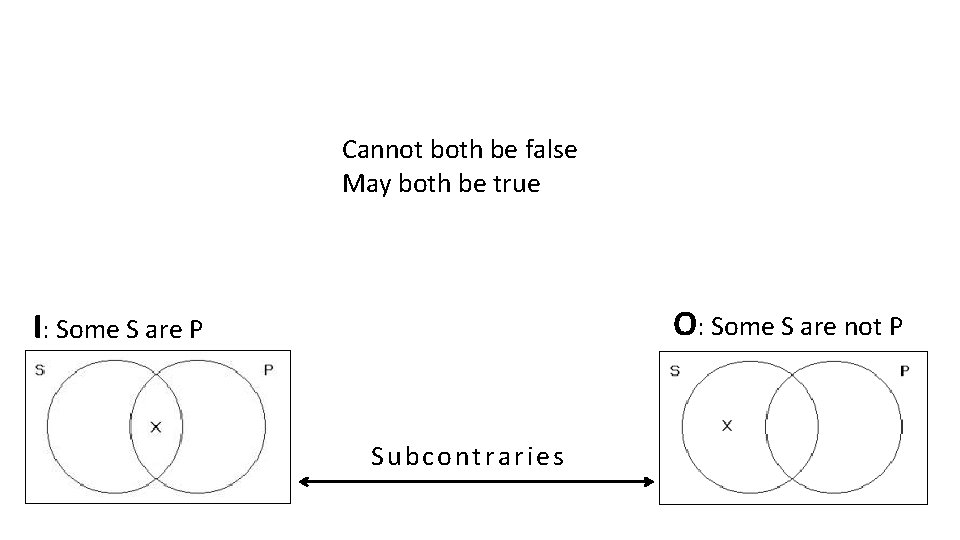
Cannot both be false May both be true O: Some S are not P I: Some S are P Subcontraries

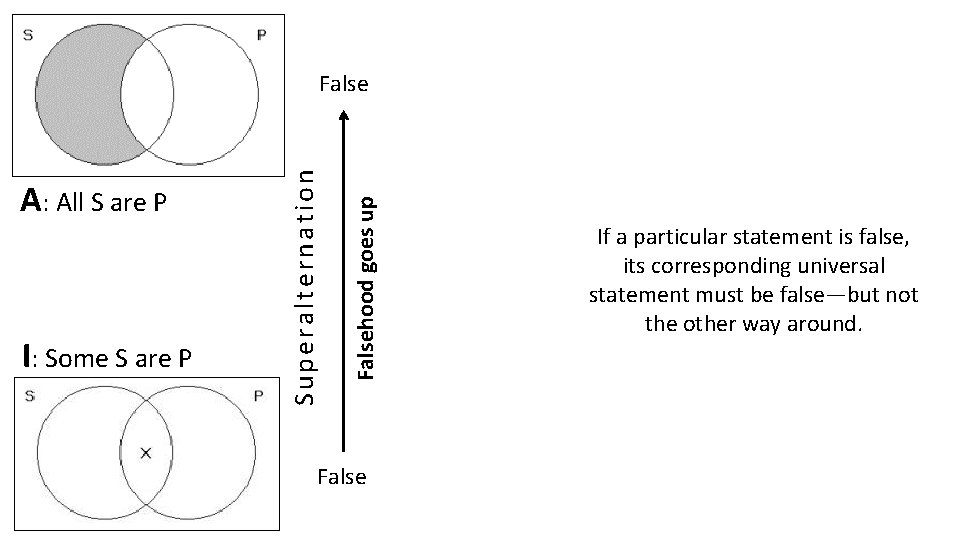
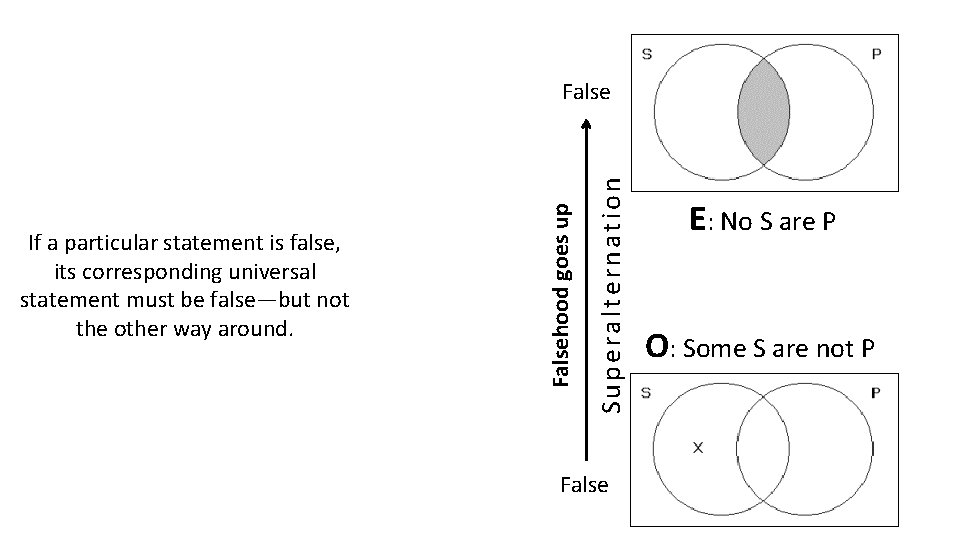
4. Superalternation If a particular statement is false, its corresponding universal statement must be false—but not the other way around.

I: Some S are P Falsehood goes up A: All S are P Superalternation False If a particular statement is false, its corresponding universal statement must be false—but not the other way around.

Superalternation If a particular statement is false, its corresponding universal statement must be false—but not the other way around. Falsehood goes up False E: No S are P O: Some S are not P

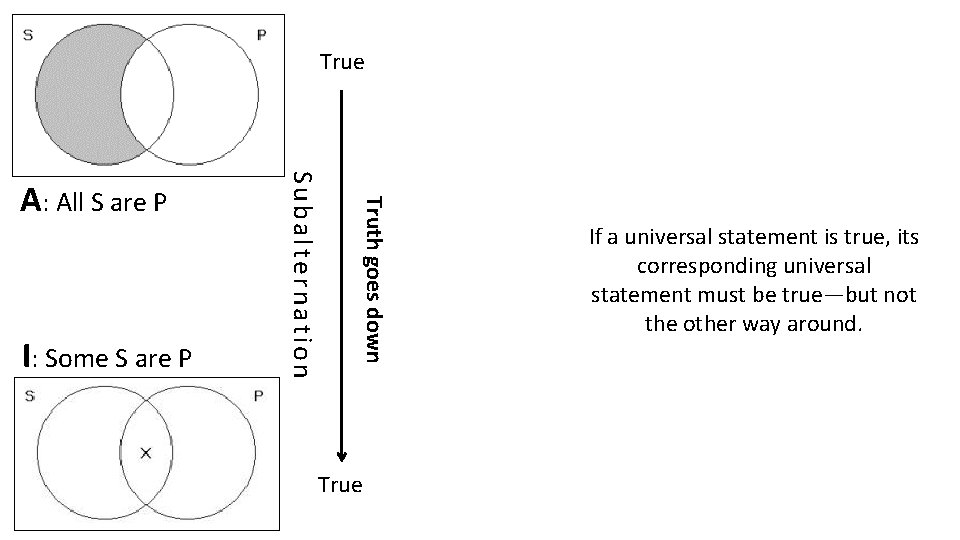
5. Subalternation If a universal statement is true, its corresponding particular statement must be true—but not the other way around.

True Truth goes down I: Some S are P Subalternation A: All S are P True If a universal statement is true, its corresponding universal statement must be true—but not the other way around.

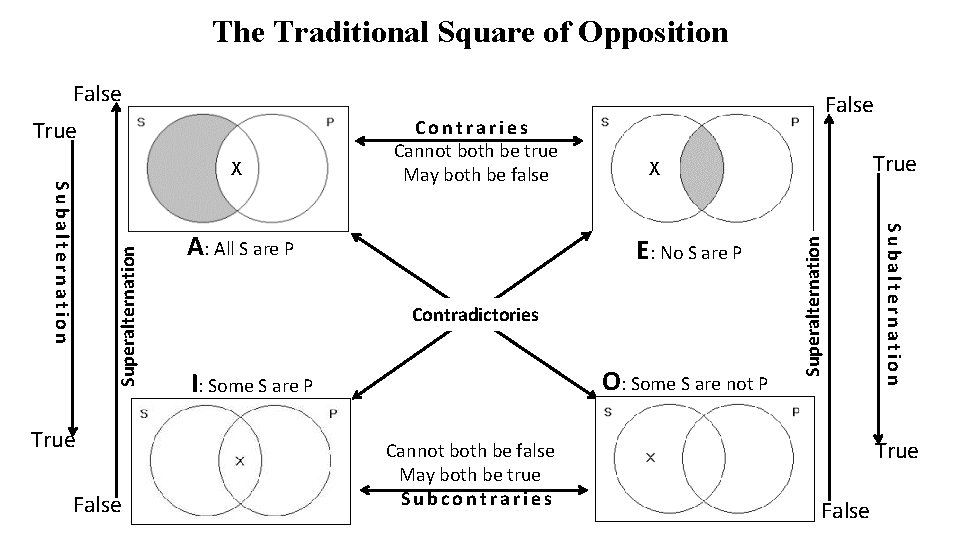
THE TRADITIONAL SQUARE OF OPPOSITION

The Traditional Square of Opposition False True False A: All S are P E: No S are P Contradictories O: Some S are not P I: Some S are P Cannot both be false May both be true Subcontraries True X Subalternation Superalternation X Contraries Cannot both be true May both be false Superalternation True False

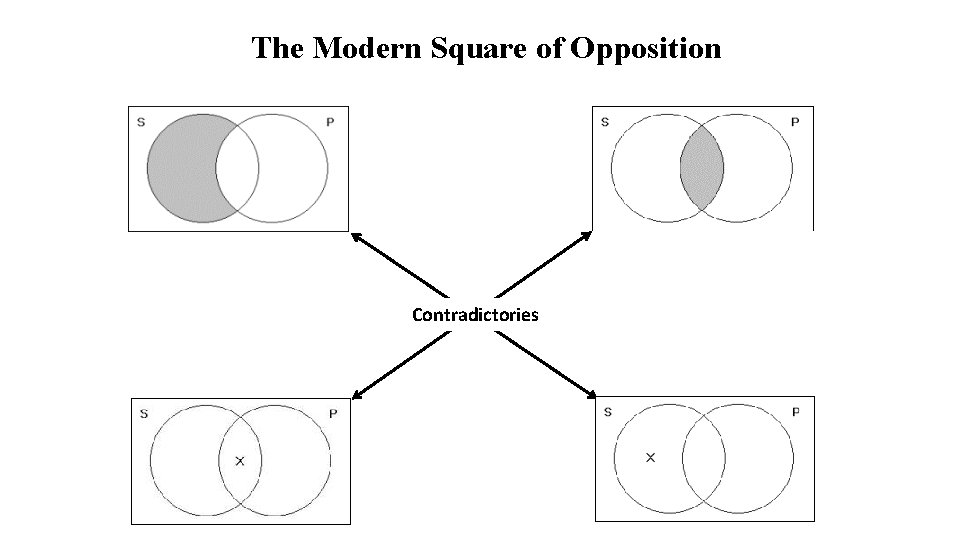
THE MODERN SQUARE OF OPPOSITION

• The traditional square of opposition enables us to determine a number of relations among the four categorical forms. • But these relations depend on whether we make what is called an existential assumption or existential import. • An existential assumption (or import) means assuming that the entities indicated by the subject are in existence. • A-form asserts that all members in the category of the subject are members of the category of the predicate. In other words, if the subject is “Martians” and the predicate “blond, ” then A-form says, “All Martians are blond. ”

• For modern logicians, the traditional square is limited. • We need to make assertions of things that don’t exist. – All dinosaurs – Martians – Triangles • We may rescue the traditional interpretation by using the square only for entities in existence.

• And what about this statement: “All shoplifters are prosecuted. ” • Curiously, if there are no shoplifters, the proposition is true! In other words, statements like this require that the class of the subject be empty. • Consequently, we must not make that assumption. The modern interpretation preserves the relationships of the contradictories.

The Modern Square of Opposition Contradictories

THE END