Capacity Scaling in Delay Tolerant Networks with Heterogeneous

Capacity Scaling in Delay Tolerant Networks with Heterogeneous Mobile Nodes Michele Garetto – Università di Torino Paolo Giaccone - Politecnico di Torino Emilio Leonardi – Politecnico di Torino Mobi. Hoc 2007 1

Outline Ø Introduction and motivation Ø Assumptions and notations Ø Main results Ø Some hints on the derivation of results Ø Conclusions 2

Introduction Ø The sad Gupta-Kumar result: In static ad hoc wireless networks with n nodes, the per-node throughput behaves as P. Gupta, P. R. Kumar, The capacity of wireless networks, IEEE Trans. on Information Theory, March 2000 3

Introduction Ø The happy Grossglauser-Tse result: q. In mobile ad hoc wireless networks with n nodes, the per -node throughput remains constant o assumption: uniform distribution of each node presence over the network area M. Grossglauser and D. Tse, Mobility Increases the Capacity of Ad Hoc Wireless Networks, IEEE/ACM Trans. on Networking, August 2002 4

Introduction Ø Node mobility can be exploited to carry data across the network q Store-carry-forward communication scheme S R D Ø Drawback: large delays (minutes/hours) q Delay-tolerant networking 5

Mobile Ad Hoc (Delay Tolerant) Networks Ø Have recently attracted a lot of attention Ø Examples qpocket switched networks (e. g. , i. Motes) qvehicular networks (e. g. , cars, buses, taxi) qsensor networks (e. g. , disaster-relief networks, wildlife tracking) q. Internet access to remote villages (e. g. , IP over usb over motorbike) 6

The general (unanswered) problem Ø Key issue: how does network capacity depend on the nodes mobility pattern? Ø Are there intermediate cases in between extremes of static nodes (Gupta-Kumar’ 00) and fully mobile nodes (Grossglauser-Tse’ 01)? 7

Outline Ø Introduction and motivation Ø Assumptions and notations Ø Main results Ø Some hints on the derivation of results Ø Conclusions 8

Assumptions q n nodes moving over closed connected region q independent, stationary and ergodic mobility processes q uniform permutation traffic matrix: each node is origin and destination of a single traffic flow with rate l (n) bits/sec source node destination node l l l q all transmissions employ the same nominal range or power q all transmissions occur at common rate r q single channel, omni-directional antennas 9

Protocol Model q Let dij denote the distance between node i and node j, and RT the common transmission range q A transmission from i to j at rate r is successful if: for every other node k simultaneously transmitting RT i j (1+Δ)RT k 10

Realistic mobility models for DTNs q characterized by : Restricted mobility of individual nodes: Non-uniform density due to concentration points From: J. H. Kang, W. Welbourne, B. Stewart, G. Borriello, Extracting Places from Traces of Locations, ACM Mobile Computing and Communications Review, July 2005. From: Sarafijanovic-Djukic, M. Piorkowski, and M. Grossglauser, Island Hopping: Efficient Mobility-Assisted Forwarding in Partitioned Networks, , IEEE SECON 2006 11

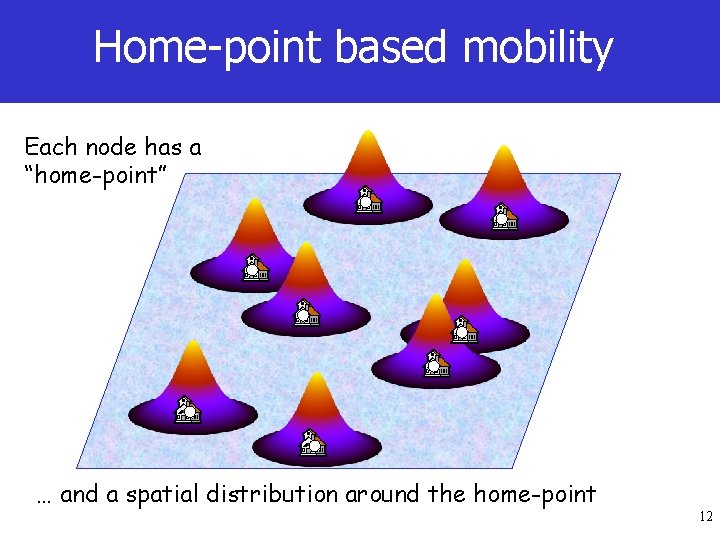
Home-point based mobility Each node has a “home-point” … and a spatial distribution around the home-point 12

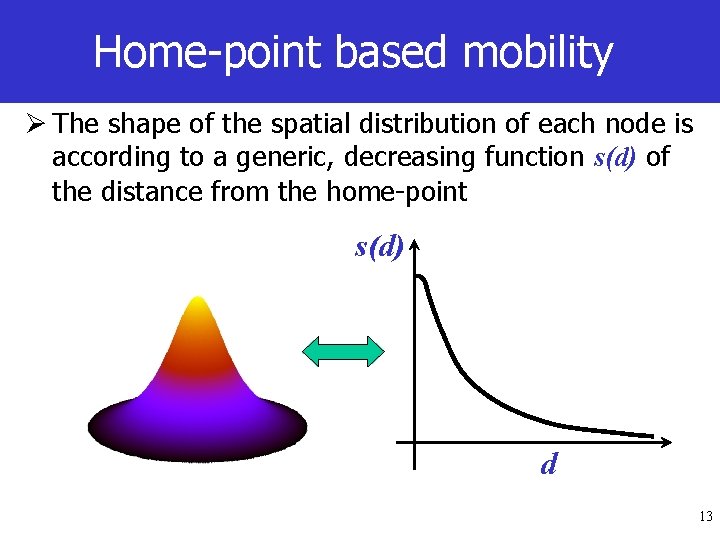
Home-point based mobility Ø The shape of the spatial distribution of each node is according to a generic, decreasing function s(d) of the distance from the home-point s(d) d 13

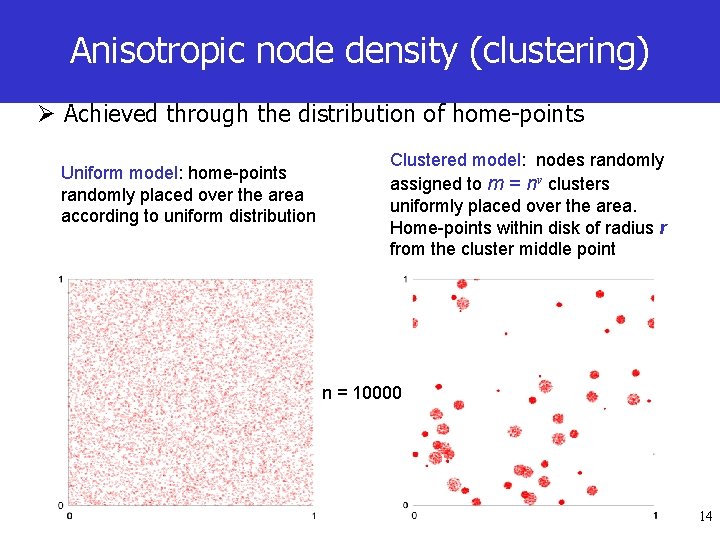
Anisotropic node density (clustering) Ø Achieved through the distribution of home-points Uniform model: home-points randomly placed over the area according to uniform distribution Clustered model: nodes randomly assigned to m = nν clusters uniformly placed over the area. Home-points within disk of radius r from the cluster middle point n = 10000 14

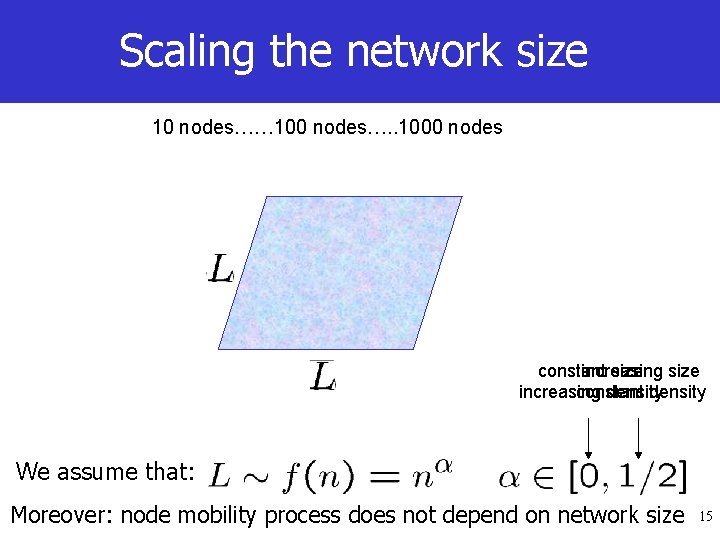
Scaling the network size 10 nodes…… 100 nodes…. . 1000 nodes constant increasing size increasing constant density We assume that: Moreover: node mobility process does not depend on network size 15

Asymptotic capacity q We say that the per-node capacity is exist two constants c and c’ such that if there q sustainable means that the network backlog remains finite q Equivalently, we say that the network capacity in this case is 16

Outline Ø Introduction and motivation Ø Assumptions and notations Ø Main results Ø Some hints on the derivation of results Ø Conclusions 17

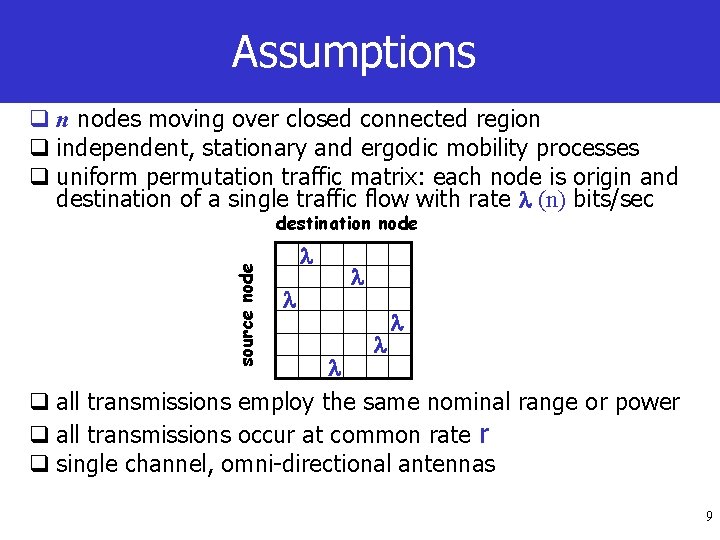
Asymptotic capacity results logn [ (n)] Uniform Model per-node capacity 0 -1/2 Independently of the shape of s(d) ! -1 0 Recall: 1/2 18

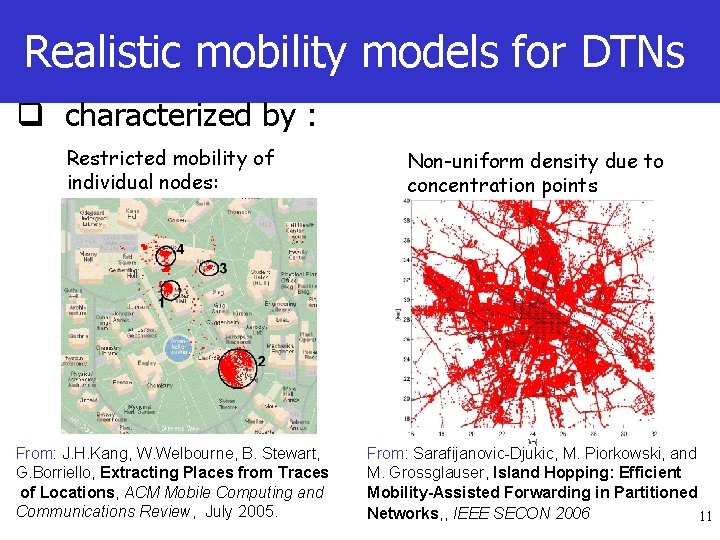
Asymptotic capacity results logn [ (n)] Clustered Model per-node capacity 0 -1/2 ? ? Lower bound : in case s(d) has finite support “Super-critical regime”: mobility helps -1 Lower bound : in case s(d) has finite support “Sub-critical regime”: mobility does not help 0 Recall: #clusters 1/2 19

Outline Ø Introduction and motivation Ø Assumptions and notations Ø Main results Ø Some hints on the derivation of results Ø Conclusions 20

A notational note Ø In the analysis we have fixed the network size, L=1 Ø and let the spatial distribution of nodes s(d) to scale with n, i. e. , s(f(n)d) f(n)=1 f(n)=2 f(n)=3 21

Uniformly dense networks q We define the local asymptotic node density ρ(XO) at point XO as: Where is the disk centered in XO , of radius q A network is uniformly dense if: 22

Properties of uniformly dense networks q Theorem: the maximum network capacity is achieved by scheduling policies forcing the transmission range to be q Corollary: simple scheduling policies leading to link capacities are asymptotically optimal, i. e. , allow to achieve the maximum network capacity (in order sense) 23

Super-critical regime q. Let (m = n in the Uniform Model) q. When we are in the supercritical regime q Theorem: in super-critical regime a random network realization is uniformely dense w. h. p. ØTransmission range ØScheduling policy S* is optimal 24

Mapping over Generalized Random Geometric Graph (GRGG) Ø Link capacities can be evaluated in terms of contact probabilities: which depend only on the distance dij between the homepoints of i and j Ø We can construct a random geometric graph in which qvertices stand for homepoints of the nodes qedges are weighted by Ø Network capacity is obtained by solving the maximum concurrent flow problem over the constructed graph 25

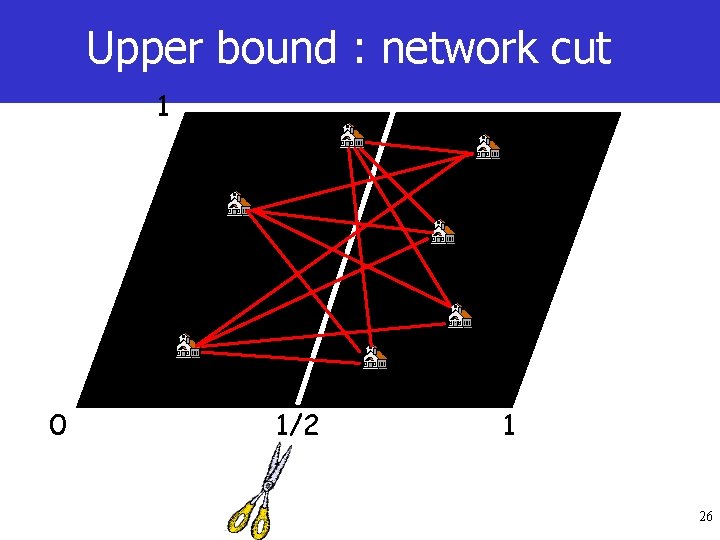
Upper bound : network cut 1 0 1/2 1 26

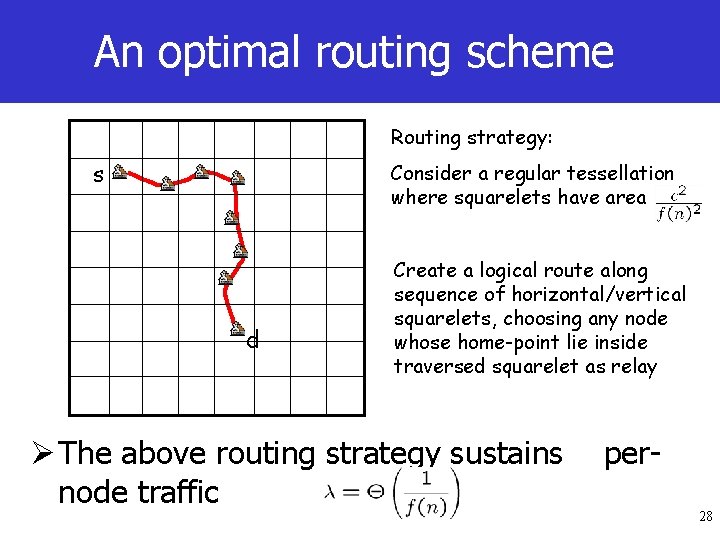
Average/random flow through the cut q The “average” flow through the cut is computed as q fundamental question: Answer: YES ! 1 Proof’s idea: Consider regular tessellation where squarelets have area γ(n) 0 1/2 1 Take upper and lower bounds for number of homepoints falling in each squarelets, combined, respectively, with lower and upper bounds of distances between homepoints belonging to different squarelets 27

An optimal routing scheme Routing strategy: s Consider a regular tessellation where squarelets have area d Create a logical route along sequence of horizontal/vertical squarelets, choosing any node whose home-point lie inside traversed squarelet as relay Ø The above routing strategy sustains node traffic per 28

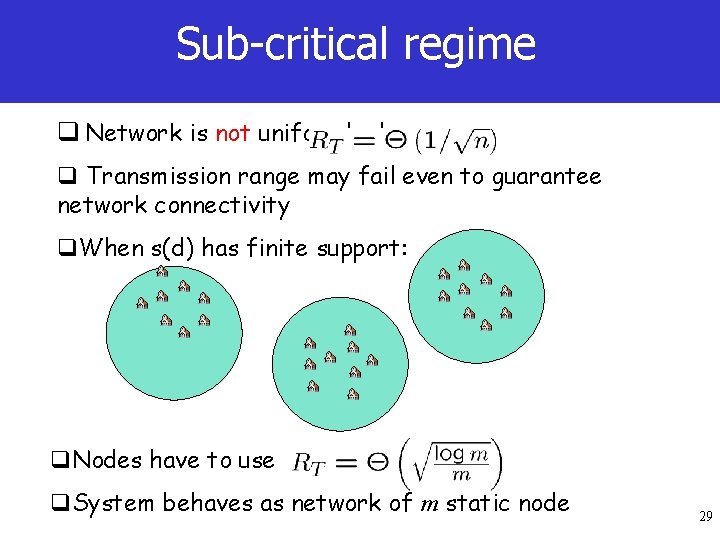
Sub-critical regime q Network is not uniformly dense q Transmission range may fail even to guarantee network connectivity q. When s(d) has finite support: q. Nodes have to use q. System behaves as network of m static node 29

Conclusions Ø We analyzed the capacity of mobile ad-hoc networks under heterogeneous nodes Ø Our study has shown the existence of two different regimes: qsuperctritical q. Subcritical Ø In this paper we have mainly focused on the supercritical regime Ø Subcritical behavior must be better explored 30

Que stio n s? ? s t n e m m o C 31