Belief Networks Kostas Kontogiannis ECE 457 Belief Networks

Belief Networks Kostas Kontogiannis E&CE 457

Belief Networks • A belief network is a graph in which the following holds: – A set of random variables makes up the nodes of the network – A set of directed links or arrows connects pairs of nodes. The intuitive meaning of an arrow from node X to node Y is that X has a direct influence on Y – Each node has a conditional probability table that quantifies the effects that the parents have on the node. The parents of a node are all those nodes that have arrows pointing to it. – The graph has no directed cycles (hence is a directed, acyclic graph, DAG)

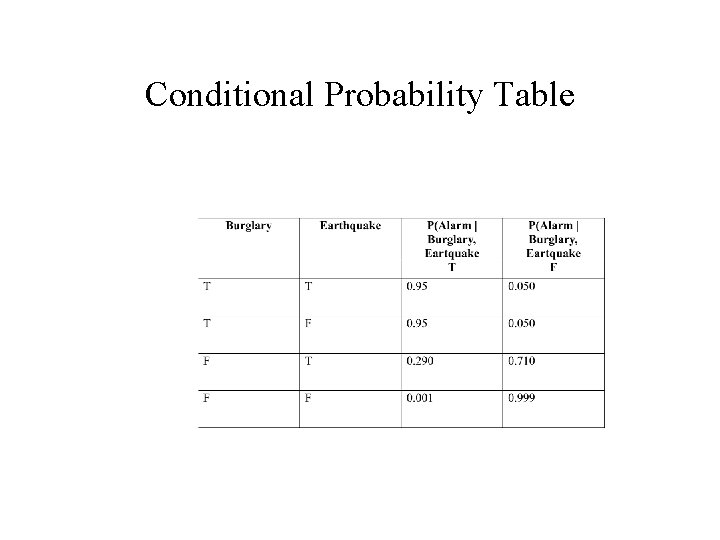
Conditional Probability Table

The Semantics of Belief Networks • Once we have specified the topology we need to specify the Conditional Probability Table for each node. Each row in the table contains the conditional probability of each node value for a conditional case. • Each row in a conditional probability table must sum to 1, because the entries represent an exhaustive set of cases for the variable. In general, a table for a Boolean variable with n Boolean parents contains 2 n independently specifiable probabilities.

Representing the Joint Probability Distribution • A belief network provides a complete description of the domain. Every entry in the joint probability distribution can be calculated from the information in the network. • The value of the probability that the random variables X 1, X 2, . . Xn have values x 1, x 2, . . Xn is given as: P(x 1, x 2, … xn) = Product i=1 n P(xi | Parents(Xi))

A Method for Constructing Belief Networks • The general procedure for incremental network construction is as follows: – Choose a set of relevant variables Xi that describe the domain – Choose an ordering for the variables – While there are variables left: • Pick a variable Xi and add a node to the network for it • Set Parent(Xi) to some minimal set of nodes already in the net such that the conditional property is satisfied • Define the conditional probability table for Xi – Conditional Probability Property P(Xi | X 1, X 2, … Xi-1) = P(Xi | Parents(Xi) provided that Parents(Xi) {X 1, X 2, … Xi-1}

Representation of Conditional Probabilities Tables • Conditional probabilities fall into one of several categories that have canonical distributions • Deterministic nodes have their values specified exactly by the values of their parents • Uncertain relationships can often characterized by socalled “noisy” logical relationships • The standard example is the noisy-or relation which is the generalization of the logical OR

Noisy-Or Assumptions • Each cause has an independent chance of causing the effect • All possible causes are listed • Whatever inhibits an cause having an effect is independent of whatever inhibits another cause having the same effect

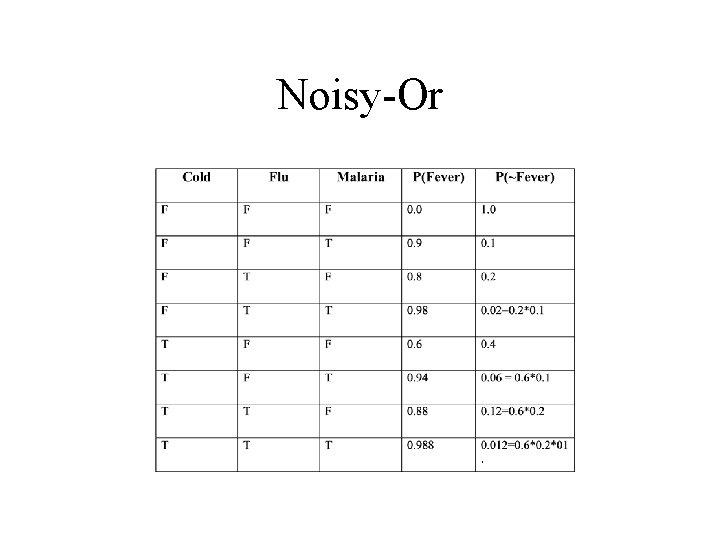
Noisy-Or