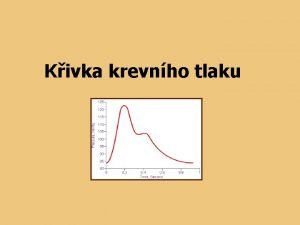
Aproximan a interpolan kivky Interpolace Kivka prochz pmo

Aproximační a interpolační křivky

Interpolace • Křivka prochází přímo zadanými body

Interpolace polynomem • Lineární – 2 body • Kvadratická – 3 body • Polynom n-tého stupně – n+1 bodů

Lineární interpolace

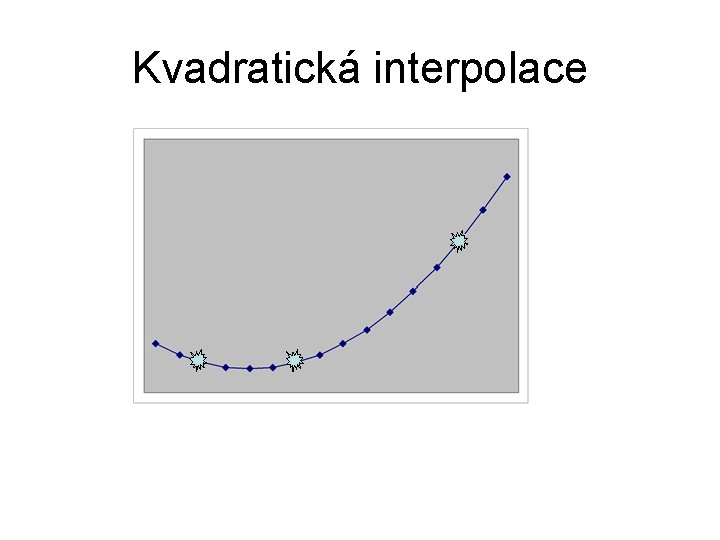
Kvadratická interpolace

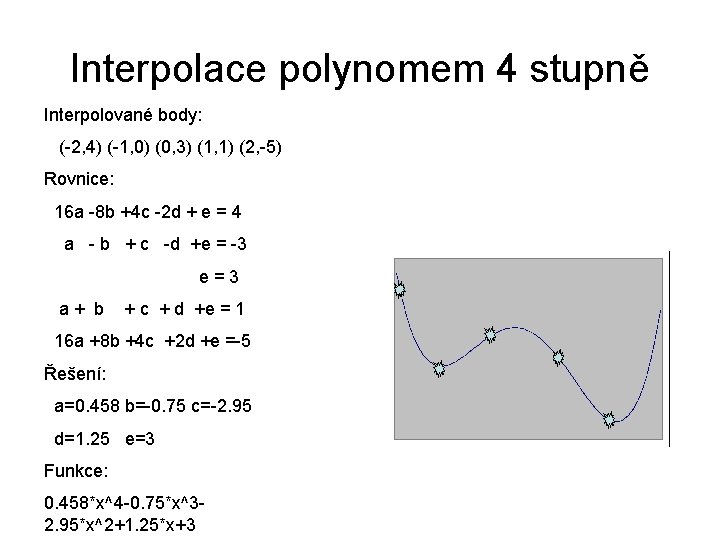
Interpolace polynomem 4 stupně Interpolované body: (-2, 4) (-1, 0) (0, 3) (1, 1) (2, -5) Rovnice: 16 a -8 b +4 c -2 d + e = 4 a - b + c -d +e = -3 e=3 a+ b + c + d +e = 1 16 a +8 b +4 c +2 d +e =-5 Řešení: a=0. 458 b=-0. 75 c=-2. 95 d=1. 25 e=3 Funkce: 0. 458*x^4 -0. 75*x^32. 95*x^2+1. 25*x+3

Spline křivka • Křivka se skládá z úseků vyjádřených polynom nižšího stupně, než odpovídá počtu bodů. Křivky na sebe v hraničních bodech hladce navazují

Lineární „spline“ • Polynomy prvního stupně. • V hraničních bodech na sebe navazují spojitě. • Není zaručena spojitost ani první derivace. • Česky se tomu říká lomená čára

Kvadratický spline • Křivka jsou úseky parabol. • V hraničních bodech na sebe paraboly hladce navazují – mají spojitou první derivaci. • Další derivace nemusí být (a obvykle nejsou) spojité. • Je nejpoužívanější, pokud se řekne jen spline, myslí se obvykle kvadratický spline (viz Auto. CAD)

Kvadratický spline

Spline křivky vyšších stupňů • Kubický – funkce po částech 3 -tího stupně (kubika), zaručuje spojitost první a druhé derivace • Obecný (n-tého stupně), zaručuje spojitost (n-1). derivace.

Aproximační křivky • Nemusí procházet přímo zadanými body. • Formálně lze za aproximační křivku považovat libovolnou křivku. • Problém je nalézt takové vyjádření, které bude – Jednoduché – Bude dostatečně dobře aproximovat danou křivku

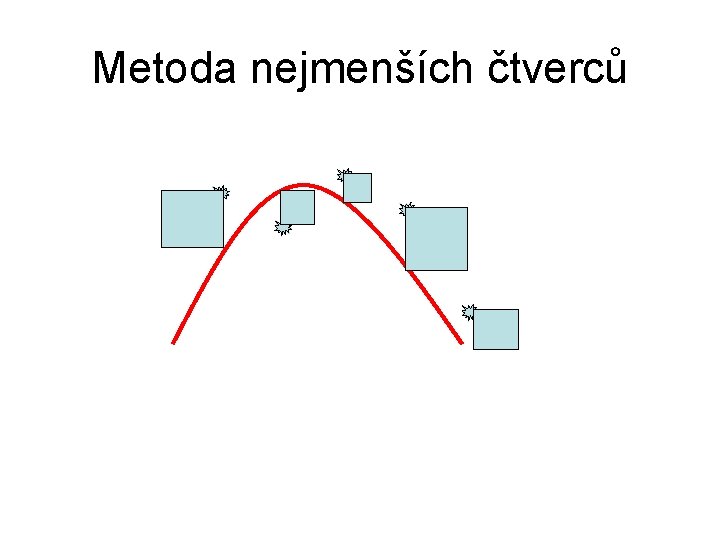
Aproximace metodou nejmenších čtverců • Zvolím typ funkce (obvykle polynom nižšího stupně, než by byl potřeba pro interpolaci bodů). • Vypočítám takové parametry, aby součet čtverců odchylek v zadaných bodech byl minimální. • ∑(yi-f(xi))2→ min

Metoda nejmenších čtverců

Bézierova aproximace (Bézierova křivka) • Aproximace polynomem daného stupně n -tý stupeň pro n+1 bodů P 0, P 1, …, Pn • Křivka prochází krajními body P 0 a Pn • Tečna v počátečním bodě P 0 je rovnoběžná s vektorem P 0 P 1. • Tečna v koncovém bodě Pn je rovnoběžná s vektorem Pn-1 Pn • Celá křivka leží v konvexním obalu bodů P 0, … , Pn

Pierre Ettiene Bézier (1910 -1999)

Vyjádření Bézierovy křivky

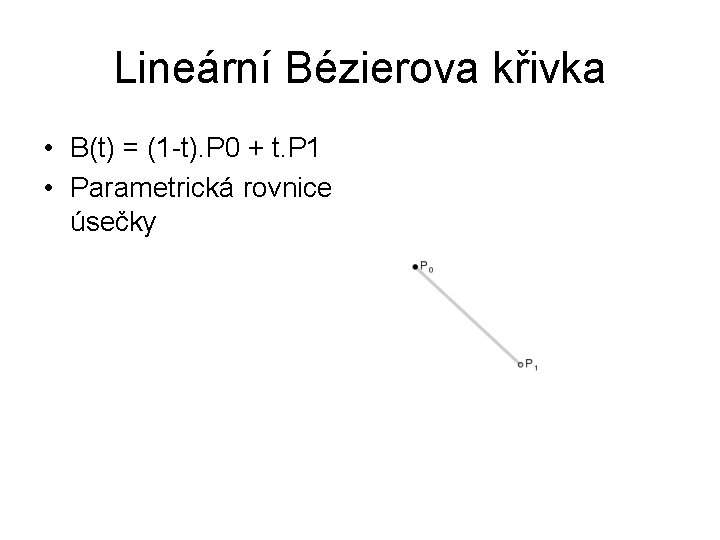
Lineární Bézierova křivka • B(t) = (1 -t). P 0 + t. P 1 • Parametrická rovnice úsečky

Kvadratická Bézierova křivka • B(t) = (1 -t)2 P 0 + 2 t(1 -t)P 1 + t 2 P 2

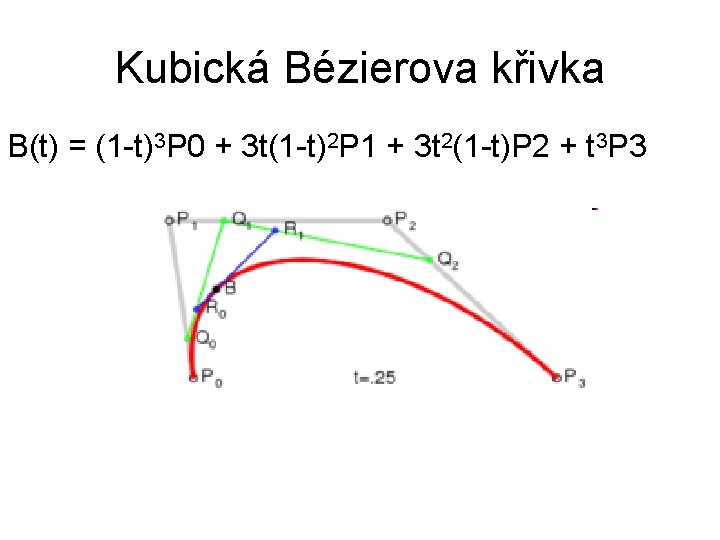
Kubická Bézierova křivka B(t) = (1 -t)3 P 0 + 3 t(1 -t)2 P 1 + 3 t 2(1 -t)P 2 + t 3 P 3

Bézierovy křivky vyšších řádů • Příklad vzorce pro křivku 5. stupně

B-spline • Úseky Bézierových křivek nižších stupňů (obvykle kvadratické a kubické křivky) budou v krajních bodech na sebe hladce navázány.

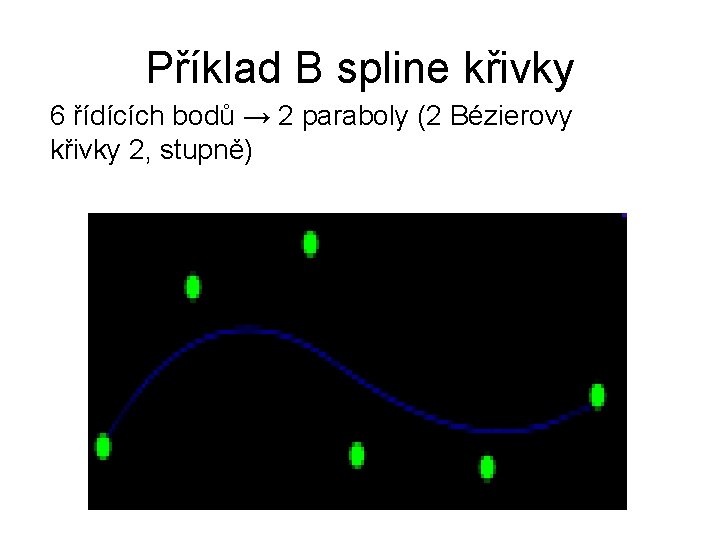
Příklad B spline křivky 6 řídících bodů → 2 paraboly (2 Bézierovy křivky 2, stupně)