Approximate Distance Oracles Mikkel Thorup and Uri Zwick

Approximate Distance Oracles Mikkel Thorup and Uri Zwick Presented By Shiri Chechik

Approximate Distance Oracles Consider a graph G=(V, E). An approximate distance oracle with a stretch k for the graph G is a data-structure that can answer an approximate distance query for any two vertices with a stretch of at most k. For every u, v in V the data structure returns in “short time” an approximate distance d’ such that: d. G(u, v) d’ k· d. G(u, v).

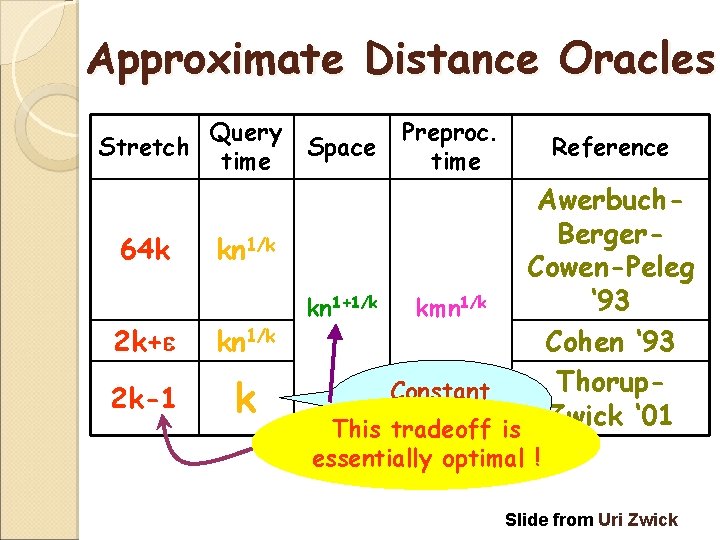
Approximate Distance Oracles Stretch Query time 64 k kn 1/k 2 k+ kn 1/k 2 k-1 k Space Preproc. time Reference Awerbuch. Berger. Cowen-Peleg ‘ 93 kn 1+1/k kmn 1/k Cohen ‘ 93 Thorup. Constant time!is Zwick ‘ 01 Thisquery tradeoff essentially optimal ! Slide from Uri Zwick

Spanners - Formal Definition Consider a graph G=(V, E) with positive edge weights. A subgraph H is a k-spanner of G if for every u, v in V: d. H(u, v) k·d. G(u, v).

Spanners - Example v

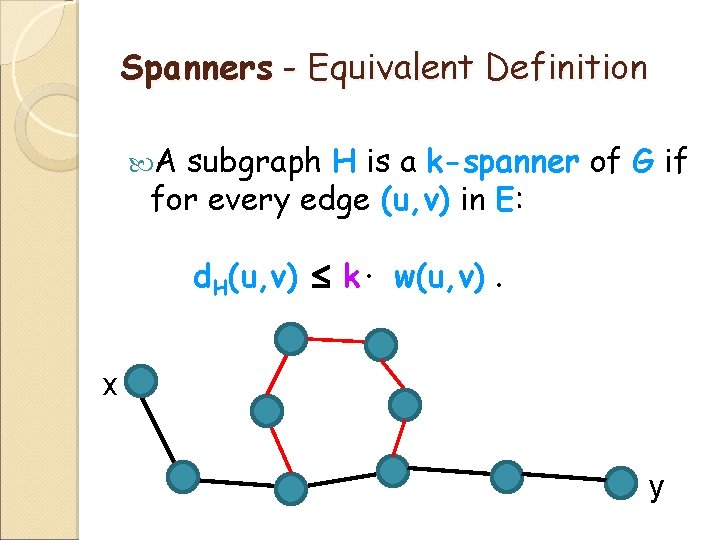
Spanners - Equivalent Definition A subgraph H is a k-spanner of G if for every edge (u, v) in E: d. H(u, v) k· w(u, v). x y

Spanners for General graphs Theorem One can efficiently find a (2 k-1)-spanner with at most n 1+1/k edges.

Spanners for General graphs Girth Conjecture (Erdös and others): There are n-vertex graphs with Ω(n 1+1/k) edges that have girth > 2 k. Known for k=1, 2, 3, 5.

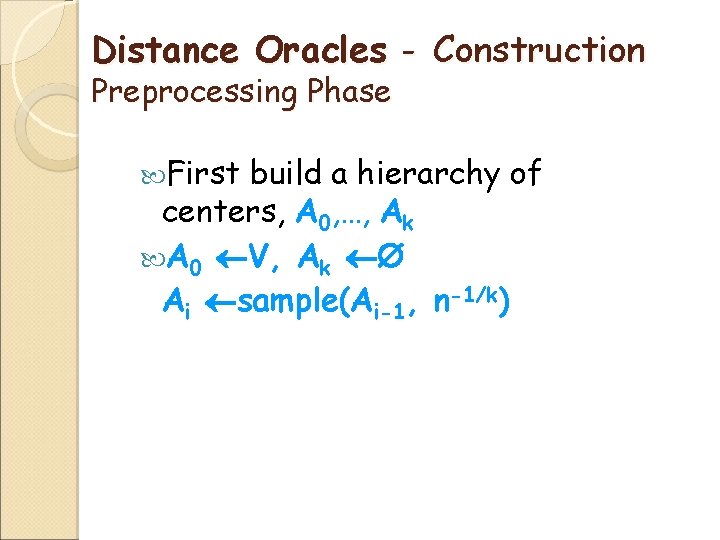
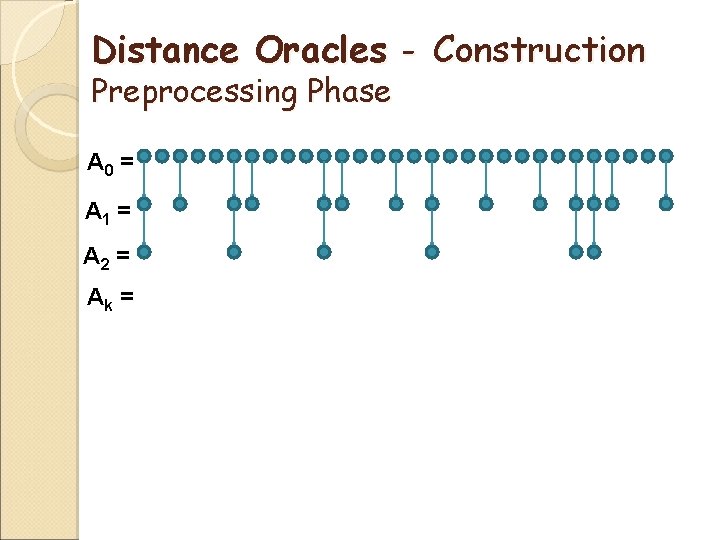
Distance Oracles - Construction Preprocessing Phase First build a hierarchy of centers, A 0, …, Ak A 0 V, Ak Ai sample(Ai-1, n-1/k)

Distance Oracles - Construction Preprocessing Phase A 0 = A 1 = A 2 = Ak =

A hierarchy of centers A 0 V ; Ak ; Ai sample(Ai-1, n-1/k) ; Slide from Uri Zwick

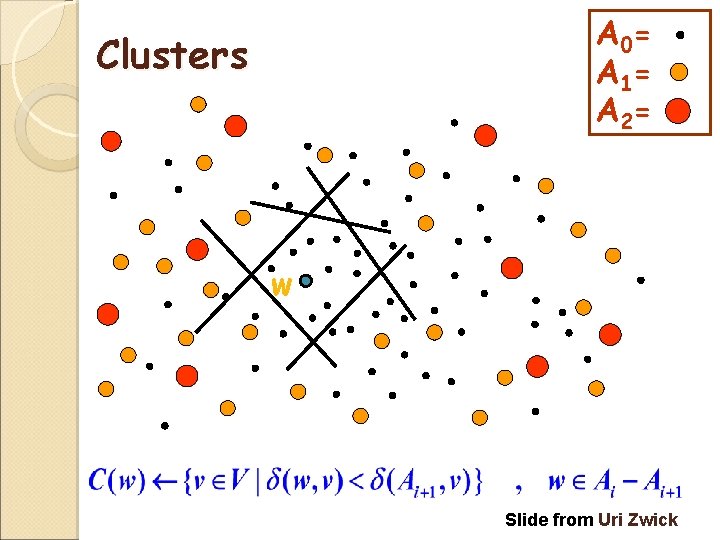
Distance Oracles - Construction Preprocessing Phase Notations pi(v) is the closest node to v in Ai For each w AiAi+1 ◦ C(w) {v| δ(v, w) < δ(v, pi+1(v))}

A 0= A 1= A 2= Clusters w Slide from Uri Zwick

Bunches (inverse clusters) Slide from Uri Zwick

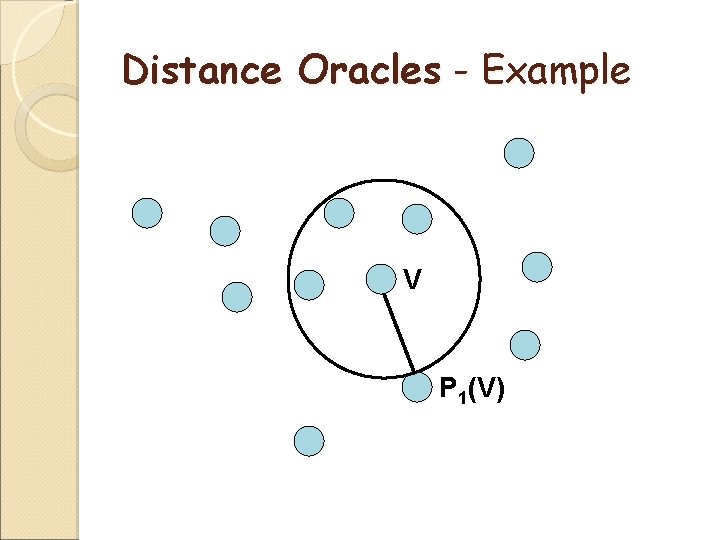
Distance Oracles - Example V P 1(V)

Distance Oracles - Example A 0 = {v 1, v 2, v 3, v 4} A 1 = {v 2, v 3} A 2 = {v 3} A 3 = {} V 3 1 2 V 4 1 1. 5 V 1 C(v 1)= {v 1, v 4}, C(v 4)= {v 4} C(v 2)= {v 2, v 1} C(v 3)= {v 1, v 2, v 3, v 4}

Distance Oracles - Construction Preprocessing Phase Data structures For every v V ◦ p 1(v), …, pk-1(v) and the distance from v to pi(v). ◦ C(v) (hash table) and the distance from v to every u in C(v).

Distance Oracles Lemma: E[|B(v)|]≤kn 1/k |B(v) Ai| is stochastically dominated by a geometric random variable with parameter p=n-1/k. Slide from Uri Zwick

Distance Oracles Lemma For every two nodes u and v, there exists a node w such that ◦ u, v C(w) ◦ The distance from u to w and from v to w is at most k·d(u, v)

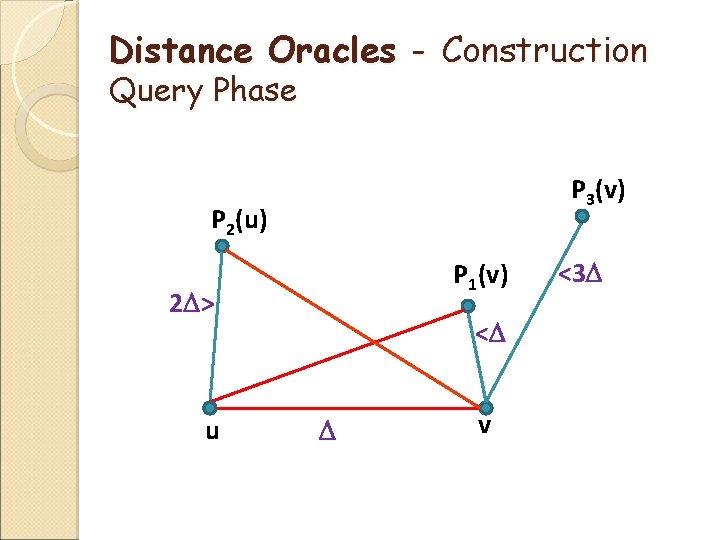
Distance Oracles - Construction Query Phase

Distance Oracles - Construction Query Phase P 3(v) P 2(u) P 1(v) 2 > u < v <3

Distance Oracles - Example What is δ(v 4, v 1)? Is v 1 C(v 4)? w = p 1 (v 1) = v 2 Is v 4 C(v 2)? w = p 2(v 4) = v 3 Is v 1 C(v 3)? – Yes V 3 1 2 V 4 1 1. 5 V 1 C(v 1)= {v 1, v 4}, C(v 4)= {v 4} C(v 2)= {v 2, v 1} C(v 3)= {v 1, v 2, v 3, v 4}

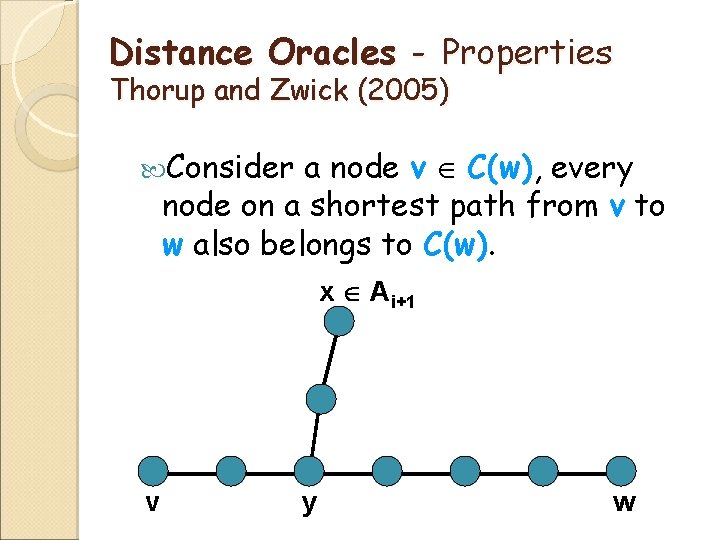
Distance Oracles - Properties Thorup and Zwick (2005) Consider a node v C(w), every node on a shortest path from v to w also belongs to C(w). x Ai+1 v y w

Distance Oracles - Properties Thorup and Zwick (2005) v belongs to C(pi(v)) for every 0≤ i ≤k-1.

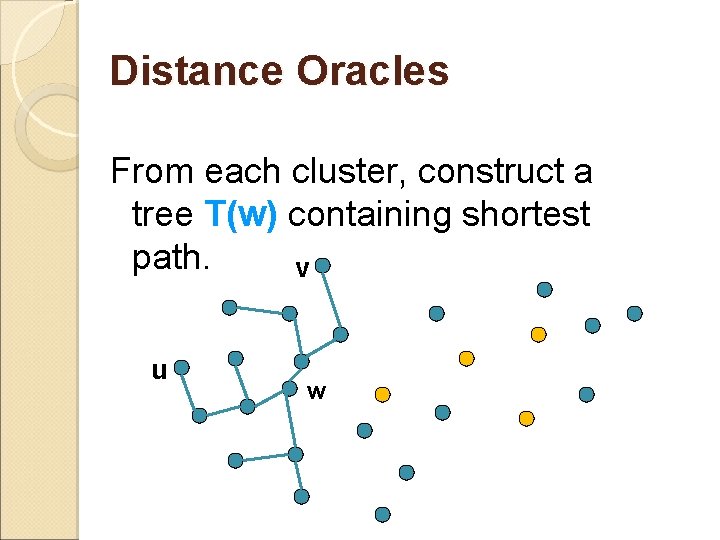
Distance Oracles From each cluster, construct a tree T(w) containing shortest path. v u w

Distance Oracles The union of all these trees is a (2 k-1)-spanner with O(kn 1+1/k) edges.