Approximate Distance Oracles Mikkel Thorup ATT Research Uri

Approximate Distance Oracles Mikkel Thorup AT&T Research Uri Zwick Tel Aviv University 1

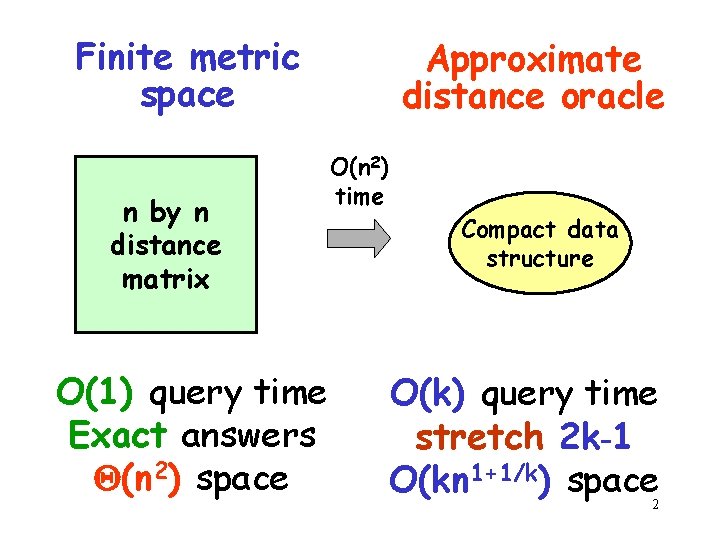
Finite metric space n by n distance matrix O(1) query time Exact answers (n 2) space Approximate distance oracle O(n 2) time Compact data structure O(k) query time stretch 2 k-1 O(kn 1+1/k) space 2

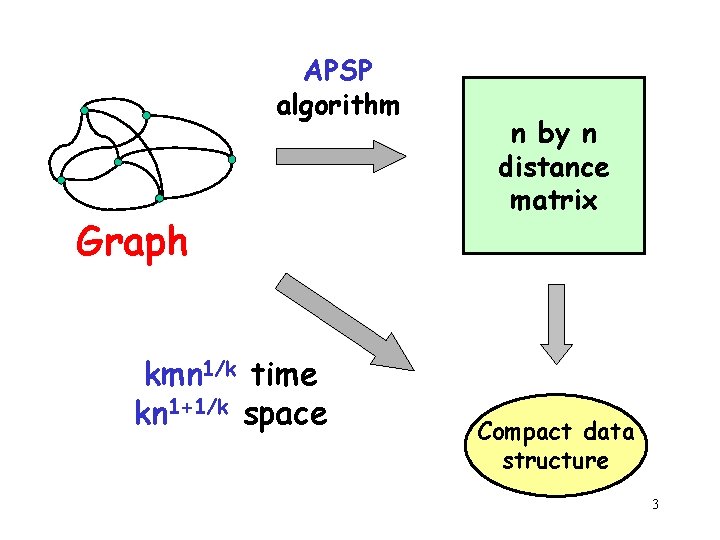
APSP algorithm Graph kmn 1/k time kn 1+1/k space n by n distance matrix Compact data structure 3

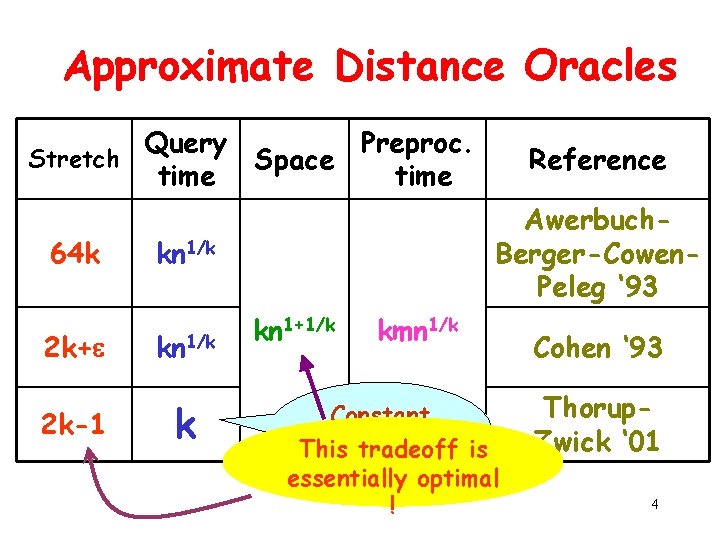
Approximate Distance Oracles Query Preproc. Stretch Space time 64 k Awerbuch. Berger-Cowen. Peleg ‘ 93 kn 1/k 2 k+ kn 1/k 2 k-1 k Reference kn 1+1/k kmn 1/k Constant query time! is This tradeoff essentially optimal ! Cohen ‘ 93 Thorup. Zwick ‘ 01 4

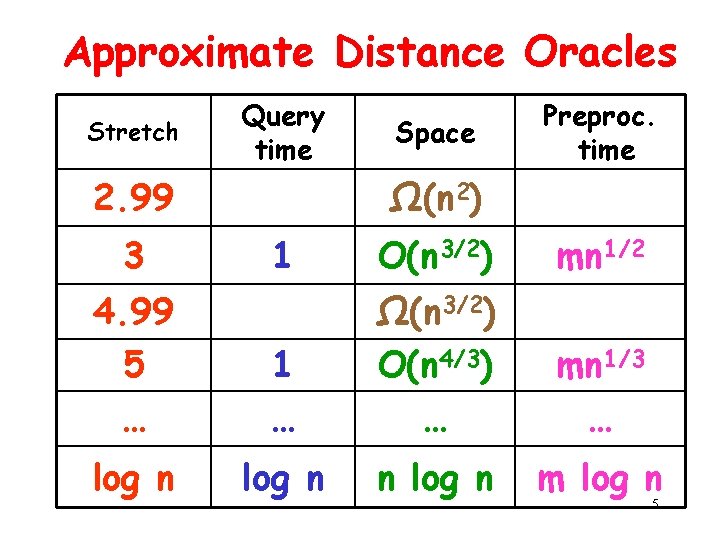
Approximate Distance Oracles Stretch Query time 2. 99 3 Space Preproc. time Ω(n 2) 1 O(n 3/2) mn 1/2 4. 99 5 … 1 … Ω(n 3/2) O(n 4/3) … mn 1/3 … log n n log n m log n 5

Stretch/space tradeoff Let G=(V, E) be a graph with |V|=n and girth(G)≥ 2 k+2. Any subgraph G’=(V, E’) of G must have a distinct data structure! If (u, v) E’, then G’(u, v)=1. Otherwise G’(u, v) ≥ 2 k+1. As there are 2|E| different subgraphs of G, some subgraphs must have data structures of at least |E| bits. Conjecture: (Erdös ’ 65) For every k≥ 1, there are infinitely many n-vertex graphs with Ω(n 1+1/k) edges that have girth≥ 2 k+2. 6

Spanners Let G be a weighted undirected graph. A subgraph H of G is a t-spanner of G iff u, v G, H(u, v) t G(u, v). Awerbuch ’ 85 Peleg-Schäffer ‘ 89 7

Trivial example 8

Theorem For every k≥ 1, every weighted undirected graph on n vertices has a (2 k-1)-spanner with at most m 2 k+1(n) ≤ n 1+1/k edges. Maximal number of edges in an n-vertex graph with girth ≥ 2 k+1 Tight for k=1, 2, 3, 5. Conjectured to be tight for any k 9

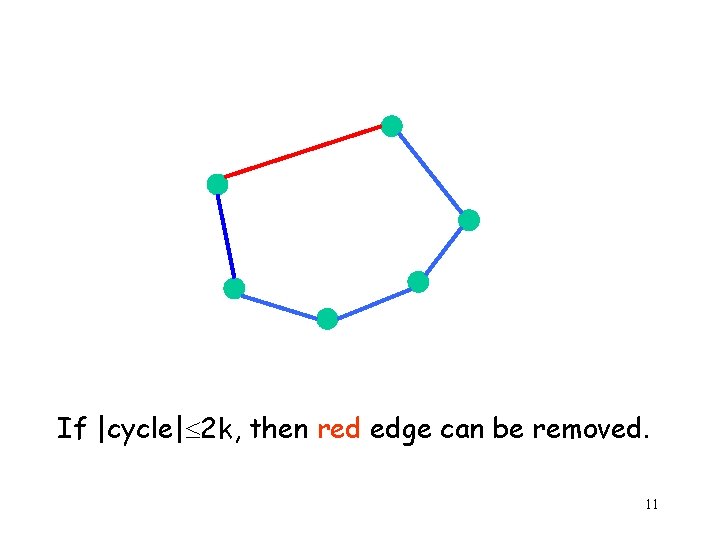
Proof/Algorithm: Consider the edges in non-decreasing order of weight. Add each edge to the spanner if it does not close a cycle of size at most 2 k. The resulting graph is a (2 k-1)-spanner and it does not contain a cycle of size at most 2 k. Hence the number of edges is at most m 2 k+1(n) ≤ n 1+1/k. [Althöfer, Das, Dobkin, Joseph, Soares ‘ 93] 10

If |cycle| 2 k, then red edge can be removed. 11

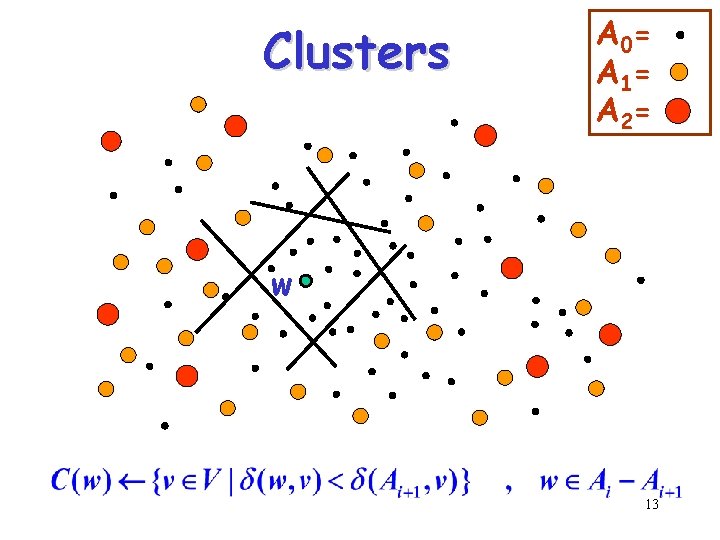
A hierarchy of centers A 0 V ; Ak ; Ai sample(Ai-1, n-1/k) ; 12

Clusters A 0= A 1= A 2= w 13

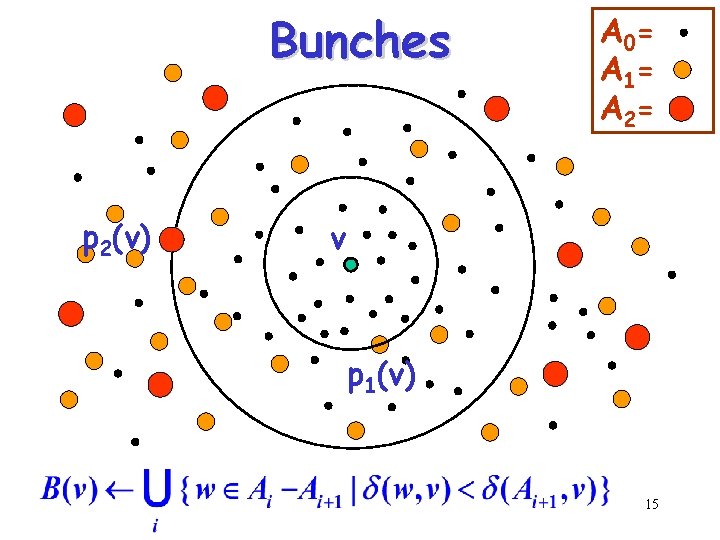
Bunches (inverse clusters) 14

Bunches p 2(v) A 0= A 1= A 2= v p 1(v) 15

The data structure For every vertex v V: • The centers p 1(v), p 2(v), …, pk-1(v) • A hash table holding B(v) For every w V, we can check, in constant time, whether w B(v), and if so, what is (v, w). 16

Lemma: E[|B(v)|]≤kn 1/k Proof: |B(v) Ai| is stochastically dominated by a geometric random variable with parameter p=n-1/k. 17

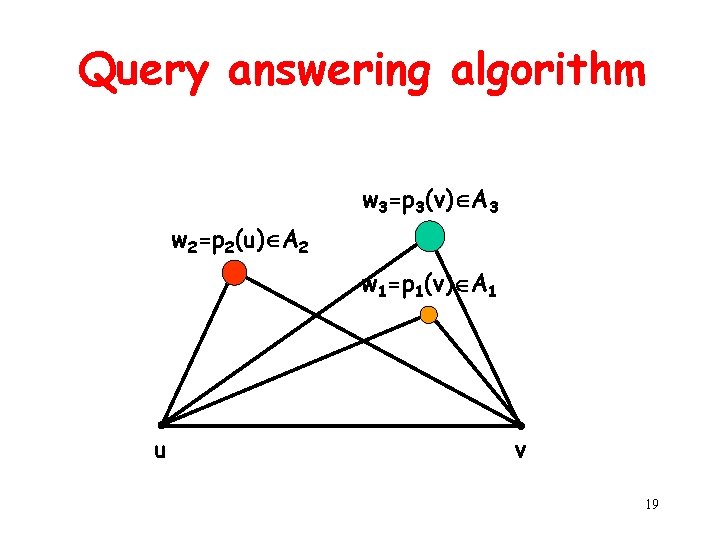
Query answering algorithm Algorithm distk(u, v) w u , i 0 while w B(v) { i i+1 (u, v) (v, u) w pi(u) } return (w, u)+ (w, v) 18

Query answering algorithm w 3=p 3(v) A 3 w 2=p 2(u) A 2 w 1=p 1(v) A 1 u v 19

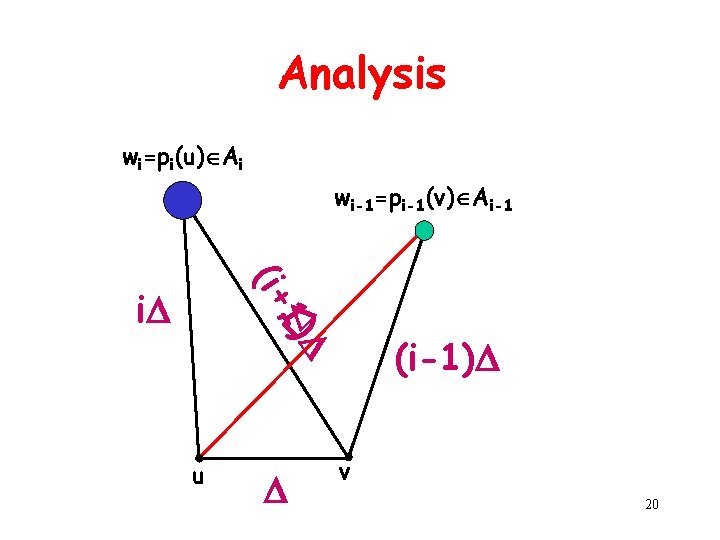
Analysis wi=pi(u) Ai wi-1=pi-1(v) Ai-1 (i+ i 1) i (i-1) u v 20

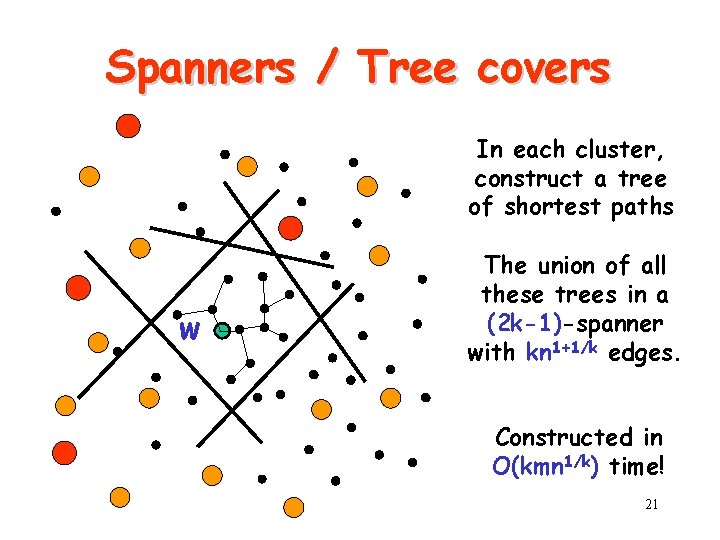
Spanners / Tree covers In each cluster, construct a tree of shortest paths w The union of all these trees in a (2 k-1)-spanner with kn 1+1/k edges. Constructed in O(kmn 1/k) time! 21

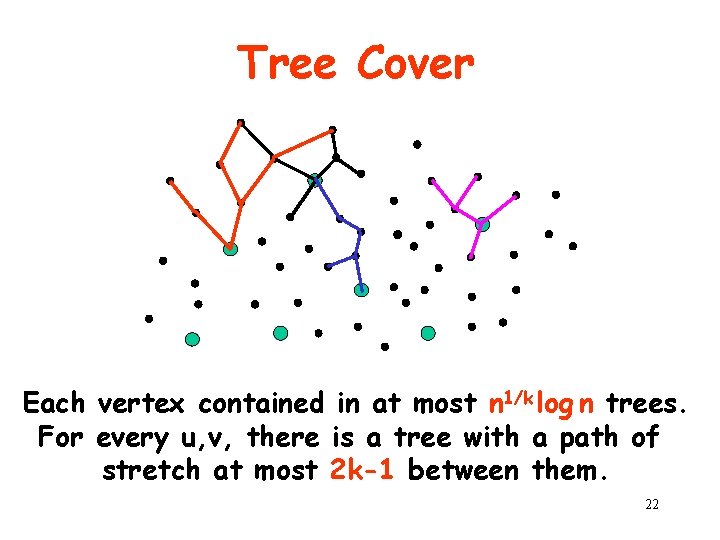
Tree Cover Each vertex contained in at most n 1/k log n trees. For every u, v, there is a tree with a path of stretch at most 2 k-1 between them. 22

Applications • • • Routing Distance labels Sub-quadratic approximation algorithms for metric space problems 23

Open Problems 1. Deterministic construction of (2 k-1, n 1+1/k, k)-distance oracles in o(mn) time? 2. Constructing a (3, n 3/2, 1)-distance oracle in n 2+o(1) time? 3. Distance oracles with additive errors? 24