Antonio Covello qualche elemento su monocordo e la

Antonio Covello qualche elemento su monocordo e la scala musicale pitagorica Pitagora Raffaello Sanzio (1483 -1520) : La Scuola di Atene (1509 -1510), Palazzo Vaticano, Stanza della Segnatura (particolare)

indice Propagazione di un impulso su una corda Riflessione di un impulso viaggiante Alcune grandezze fisiche dei fenomeni ondosi Onde stazionarie Legge di Galileo Il monocordo e la legge di Galileo I nodi (e gli armonici) “Consonanza” pitagorica Scala pitagorica La soluzione (la scala temperata) Il ciclo delle quinte

Propagazione di un impulso su una corda Impulso sinusoidale Siccome l’oscillazione è perpendicolare alla direzione del movimento dell’impulso, quest’ultimo è detto trasversale. a. covello ― qualche elemento su monocordo e scala musicale pitagorica

Riflessione di un impulso viaggiante Estremo fisso Affinché l’estremo sia fisso l’oscillazione si deve annullare, pertanto la fase si inverte. Estremo libero a. covello ― qualche elemento su monocordo e scala musicale pitagorica

Alcune grandezze fisiche dei fenomeni ondosi • Periodo, T: tempo necessario affinché si compia un’oscillazione completa. U(T) = s. • Frequenza, ν: numero di oscillazioni nell’unità di tempo. U(ν) = Hz. • Lunghezza d’onda, λ: distanza percorsa dal fronte d’onda in un periodo. U(λ) = m. • Velocità di propagazione, v: . • Ampiezza, A: massimo discostamento dalla posizione di equilibrio. U(A) dipende dalla grandezza oscillante. a. covello ― qualche elemento su monocordo e scala musicale pitagorica

Onde stazionarie Per un’onda che si propaghi in un mezzo di lunghezza finito, va considerato l’effetto che si produce quando la perturbazione raggiunge l’estremo dell’elemento oscillante. In generale, gli effetti prodotti dall’azione dei bordi sono complicati, pertanto in prima approssimazione si considera solo il caso in cui si generano configurazioni le cui caratteristiche sono costanti nello spazio e nel La tempo. perturbazione corre lungo la corda fino all’estremo fissato dove si riflette invertendo la fase. L’onda riflessa viene a sovrapporsi ad eventuali successivi impulsi periodici applicati all’estremo libero. Per un’onda stazionaria si può pensare che l’energia non si propaghi lungo la corda, ma stazioni in posizioni definite. Se, sospesa la sollecitazione da parte della sorgente, la corda cessa di vibrare è per la presenza di attriti. Questo genere di onde sono di fondamentale importanza per l’acustica musicale. a. covello ― qualche elemento su monocordo e scala musicale pitagorica

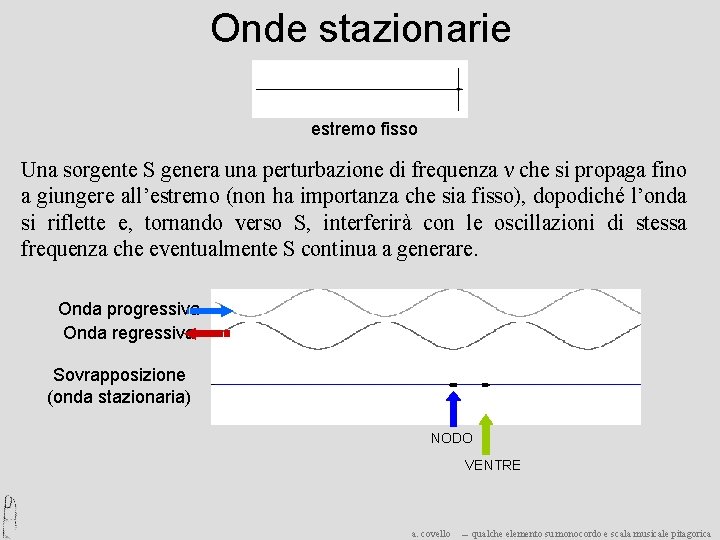
Onde stazionarie estremo fisso Una sorgente S genera una perturbazione di frequenza ν che si propaga fino a giungere all’estremo (non ha importanza che sia fisso), dopodiché l’onda si riflette e, tornando verso S, interferirà con le oscillazioni di stessa frequenza che eventualmente S continua a generare. Onda progressiva Onda regressiva Sovrapposizione (onda stazionaria) NODO VENTRE a. covello ― qualche elemento su monocordo e scala musicale pitagorica

Onde stazionarie Ricorrendo alle opportune espressioni matematiche, per descrivere un’onda stazionaria si troverebbe la seguente equazione: La quale si verifica per tutti i valori dell’argomento tali che: con n = 1, 2, 3, … cioè: o anche: Il significato è che i corrispondenti punti sulla corda non oscillano, sono fissi: NODI. Quindi, per quelle lunghezze d’onda in cui si verifica, con la lunghezza L della corda, il rapporto semplice: si ha un’onda stazionaria. a. covello ― qualche elemento su monocordo e scala musicale pitagorica

Legge di Galileo Per un’onda che si propaga lungo una corda si scopre un legame matematico fra alcune caratteristiche fisiche della corda vibrante e la frequenza di oscillazione della corda stessa: In cui: ν la frequenza di oscillazione della corda. n numero naturale L la lunghezza della corda. τ la tensione cui la corda è sottoposta. μ massa per unità di lunghezza (densità lineare della corda, in questo parametro vi sono le caratteristiche del materiale costituente la corda). Per n = 1 si parla di frequenza fondamentale (primo modo di oscillazione) e la formula precedente rappresenta la legge di Galileo. a. covello ― qualche elemento su monocordo e scala musicale pitagorica

Il monocordo Franchino Gaffurio (1451 - 1522) Pitagora, disegno da Theorica Musicae, 1492 Il monocordo è un cordofono costituito da una corda tesa con gli estremi fissati su una cassa di risonanza. L’intonazione può essere modificata mediante un ponticello mobile posto al di sotto della corda. Non si sa se l’attribuzione a Pitagora del monocordo sia corretta, comunque lo strumento fu da Pitagora usato e, per tutta l’antichità fino al medioevo, è stato uno strumento fondamentale per lo studio dell’acustica musicale. Nel basso medioevo furono aggiunte altre corde così da poter essere studiati gli intervalli e gli accordi. Con l’aggiunta di una corda scorrevole, in un estremo, su una carrucola si può verificare la legge di Galileo. a. covello ― qualche elemento su monocordo e scala musicale pitagorica

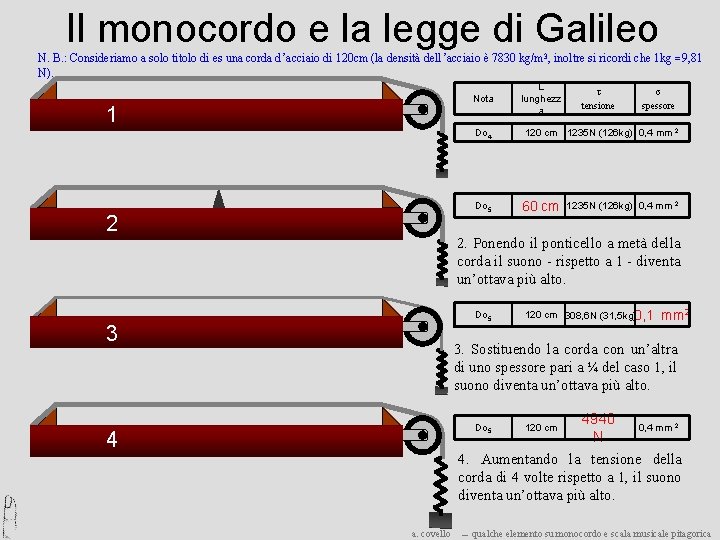
Il monocordo e la legge di Galileo N. B. : Consideriamo a solo titolo di es una corda d’acciaio di 120 cm (la densità dell’acciaio è 7830 kg/m 3, inoltre si ricordi che 1 kg = 9, 81 N). Nota 1 2 L lunghezz a τ tensione σ spessore Do 4 120 cm 1235 N (126 kg) 0, 4 mm 2 Do 5 60 cm 1235 N (126 kg) 0, 4 mm 2 2. Ponendo il ponticello a metà della corda il suono - rispetto a 1 - diventa un’ottava più alto. Do 5 3 120 cm 308, 6 N (31, 5 kg)0, 1 mm 2 3. Sostituendo la corda con un’altra di uno spessore pari a ¼ del caso 1, il suono diventa un’ottava più alto. 4940 0, 4 mm 2 N 4. Aumentando la tensione della corda di 4 volte rispetto a 1, il suono diventa un’ottava più alto. Do 5 4 a. covello ― 120 cm qualche elemento su monocordo e scala musicale pitagorica

Il monocordo e la legge di Galileo La frequenza è inversamente proporzionale alla lunghezza della corda. più lunga è una corda, minore è il numero delle vibrazioni al secondo, meno acuto risulta il suono prodotto. La frequenza è inversamente proporzionale al diametro. più una corda è spessa, minore è il numero delle vibrazioni al secondo, meno acuto il suono prodotto. La frequenza è direttamente proporzionale al quadrato della tensione. più si tende una corda, maggiore è il numero di vibrazioni al secondo, più acuto è il suono prodotto. La frequenza è inversamente proporzionale al quadrato della densità. più una corda è densa, minore è il numero delle vibrazioni al secondo, meno acuto è il suono prodotto. Si utilizzano corde sottili, corte, tese, per ottenere suoni acuti; spesse, lunghe, meno tese per ottenere suoni gravi. a. covello ― qualche elemento su monocordo e scala musicale pitagorica

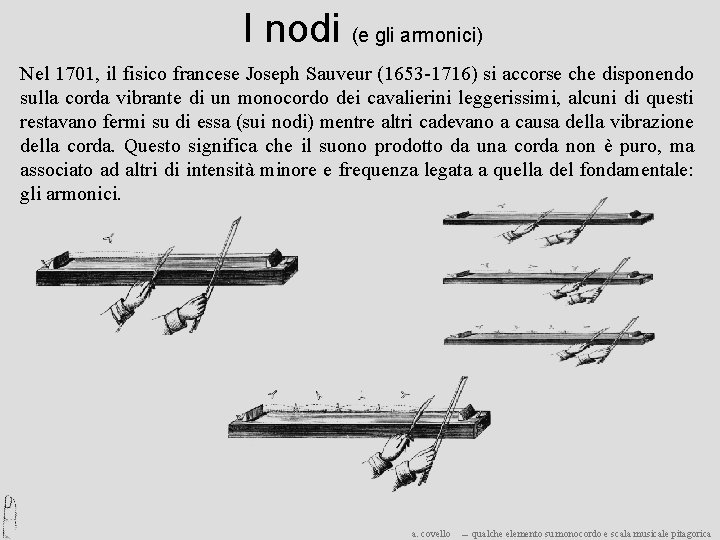
I nodi (e gli armonici) Nel 1701, il fisico francese Joseph Sauveur (1653 -1716) si accorse che disponendo sulla corda vibrante di un monocordo dei cavalierini leggerissimi, alcuni di questi restavano fermi su di essa (sui nodi) mentre altri cadevano a causa della vibrazione della corda. Questo significa che il suono prodotto da una corda non è puro, ma associato ad altri di intensità minore e frequenza legata a quella del fondamentale: gli armonici. a. covello ― qualche elemento su monocordo e scala musicale pitagorica

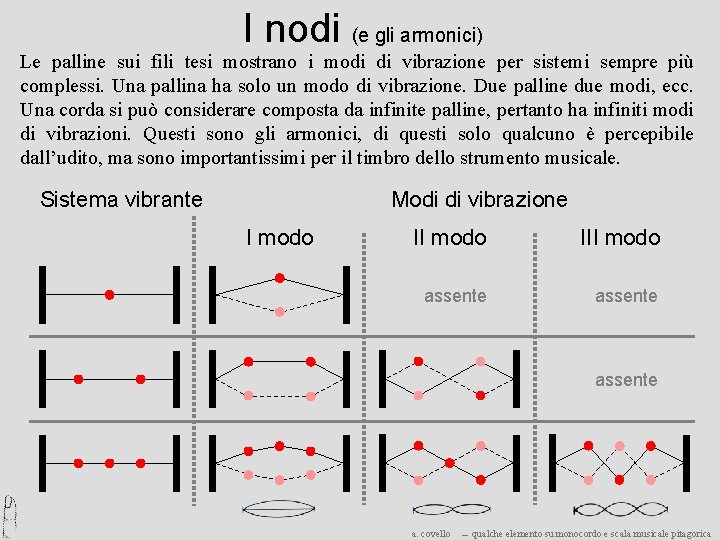
I nodi (e gli armonici) Le palline sui fili tesi mostrano i modi di vibrazione per sistemi sempre più complessi. Una pallina ha solo un modo di vibrazione. Due palline due modi, ecc. Una corda si può considerare composta da infinite palline, pertanto ha infiniti modi di vibrazioni. Questi sono gli armonici, di questi solo qualcuno è percepibile dall’udito, ma sono importantissimi per il timbro dello strumento musicale. Modi di vibrazione Sistema vibrante I modo III modo assente a. covello ― qualche elemento su monocordo e scala musicale pitagorica

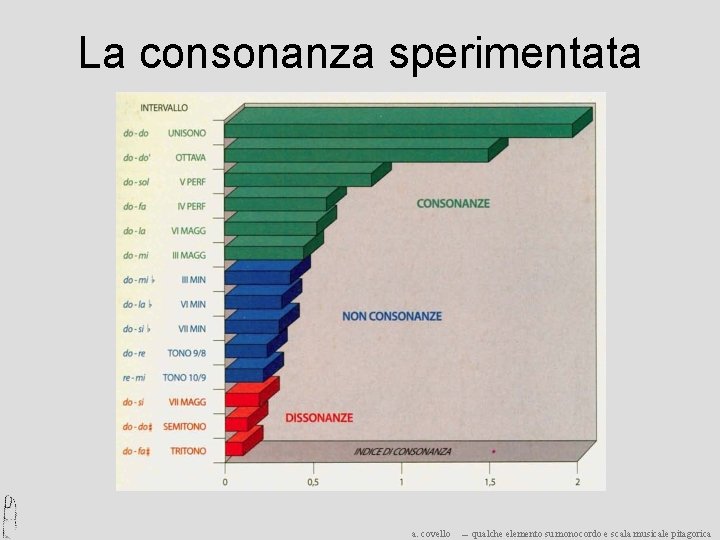
La consonanza sperimentata a. covello ― qualche elemento su monocordo e scala musicale pitagorica

La consonanza pitagorica. . . passò davanti all’officina di un fabbro e, per sorte in un certo senso divina, ebbe a udire dei martelli che battevano il ferro sull’incudine e davano dei suoni tutti in perfetto accordo armonico reciproco, in quei suoni Pitagora riconosceva gli accordi di ottava di quinta e di quarta [. . . ] entrò nell’officina e capì che la differenza tra l’altezza dei suoni dipendeva dal peso dei martelli e non dalla forza con cui si batteva, a. covello ― qualche elemento su monocordo e scala musicale pitagorica

La consonanza euclidea Sappiamo anche quali delle note siano consonanti e quali dissonanti; e quelle consonanti fanno da entrambe una sola fusione, quelle dissonanti no. Stando così le cose è ragionevole che le note consonanti, poiché appunto fanno da entrambe una sola fusione del suono, siano tra i numeri che sono in relazione tra loro in un solo nome: che sono o multipli (n: 1) o i superparticolari (n+1: n) a. covello ― qualche elemento su monocordo e scala musicale pitagorica

La consonanza euleriana Ora Vostra Altezza comprenderà facilmente che quanto più una proporzione è semplice o espressa con piccoli numeri, più essa si presenta distintamente all’intelletto suscitandovi un sentimento di piacere. Anche gli architetti osservano con la massima cura questa regola impiegando ovunque, nelle loro costruzioni, proporzioni tanto semplici quanto lo permettono le atre circostanze. a. covello ― qualche elemento su monocordo e scala musicale pitagorica

La consonanza galileiana a. covello ― qualche elemento su monocordo e scala musicale pitagorica

“Consonanza” pitagorica Pitagora trovò i rapporti esistenti tra i differenti toni scoprendo che i principali accordi consonanti erano esprimibili dai rapporti dei primi numeri interi. Facendo suonare una corda di lunghezza intera assieme ai rapporti di 4/3 (diatessaron, quarta), 3/2 (diapente, quinta), e 2/1 (diapason, ottava) di essa si ascolta la sintonia dei loro moti vibratori, questi assiemi di suoni risultano particolarmente consonanti. L = 120 cm Rapporto lunghezze Nota emessa Intervallo corde vibranti do 3 unisono l = 60 cm do 4 Ottava sol 4 quinta fa 4 quarta l’ = 80 cm l’’ = 90 cm a. covello ― qualche elemento su monocordo e scala musicale pitagorica

“Consonanza” pitagorica Se ne deduce che: data una corda vibrante di una certa lunghezza, si può ottenere un suono consonante dividendo questa: a metà, a 2/3 a ¾. L = 120 cm Rapporto lunghezze Nota emessa corde vibranti do 3 Intervallo unisono l = 60 cm do 4 Ottava sol 4 quinta fa 4 quarta l’ = 80 cm l’’ = 90 cm a. covello ― qualche elemento su monocordo e scala musicale pitagorica

Scala pitagorica In base a quanto scritto precedentemente, dato che da una corda vibrante di una certa lunghezza si può ottenere un suono consonante dividendo questa: a metà, a 2/3 a ¾, possiamo costruire la scala musicale. Si parte da una nota scelta come fondamentale e si procede di quinta in quinta. Procedere di quinta in quinta vuol dire moltiplicare la frequenza della nota data per 3/2, ovvero la lunghezza della corda per 2/3. fa 0 do 1 sol 1 fa 1 do 1 re 1 mi 1 re 2 la 2 mi 3 si 3 re 1 la 1 mi 2 si 2 mi 1 si 1 fa 1 sol 1 la 1 a. covello si 1 ― do 2 monocordo e scala musicale pitagorica

Scala pitagorica do 1 re 1 mi 1 fa 1 sol 1 la 1 si 1 do 2 Quanto vale l’intervallo fra due note successive? tono tono semitono a. covello ― monocordo e scala musicale pitagorica

Scala pitagorica Avevamo detto che partendo da una nota scelta come fondamentale e procedendo di quinta in quinta si poteva costruire la scala musicale. Per una sola ottava l’abbiamo visto, ma per generalizzare dobbiamo chiederci: partendo da una nota e procedendo per quinte arriviamo ad un nota che ha una consonanza di ottava con la nota di partenza? Ovvero, considerato che in un’ottava vi sono 12 semitoni ed in una quinta ve ne sono 7, allora, partendo da una nota e proseguendo per 12 quinte, ossia proseguendo per 7 ottave, si arriverà ad una stessa nota. Sarà vero? fa 0 do 1 sol 1 re 2 la 2 mi 3 fa#4 do#5 sol#5 si 3 re#6 la#6 mi#7 si#7 Quinte Ottave do 1 do 2 do 3 do 4 do 5 do 6 do 7 do 8 1 2 4 8 16 32 64 128 a. covello ― monocordo e scala musicale pitagorica

Scala pitagorica fa 0 do 1 sol 1 re 2 la 2 mi 3 fa#4 do#5 sol#5 si 3 re#6 la#6 mi#7 si#7 Quinte Ottave do 1 do 2 do 3 do 4 do 5 do 6 do 7 do 8 1 2 4 8 16 32 64 128 1, 01364 è detto comma diatonico o pitagorico. Il fatto che il precedente rapporto non sia 1, significa che 12 quinte non corrispondono a 7 ottave, matematicamente si dice che quinte e ottave non sono commensurabili: Musicalmente significa che nella scala pitagorica non può esistere il ciclo delle quinte. a. covello ― monocordo e scala musicale pitagorica

Scala pitagorica L’esistenza del comma pitagorico comporta che nella scala pitagorica salendo di un tono e scendendo di due semitoni non si torna alla nota di partenza. Per provarlo basta ricordare che: salire di un tono significa moltiplicare per il rapporto corrispondente delle frequenze, salire di un semitono significa moltiplicare per la radice quadrata di quello stesso rapporto: do 1 re 1 do 1 Se si osserva bene nel proseguire per semitoni compare la radice quadrata di 2! a. covello ― monocordo e scala musicale pitagorica

Il ciclo delle quinte do do# = reb si la# = sib re re# = mib la sol# = lab mi fa sol fa# = solb a. covello ― monocordo e scala musicale pitagorica

a. covello ― monocordo e scala musicale pitagorica