Analytical impedance estimates for coated surfaces SERGEY ARSENYEV

Analytical impedance estimates for coated surfaces SERGEY ARSENYEV 3 RD TOPICAL WORKSHOP ON ADVANCED LOW EMITTANCE RINGS TECHNOLOGY 2019 (ALERT 2019) IOANNINA, GREECE

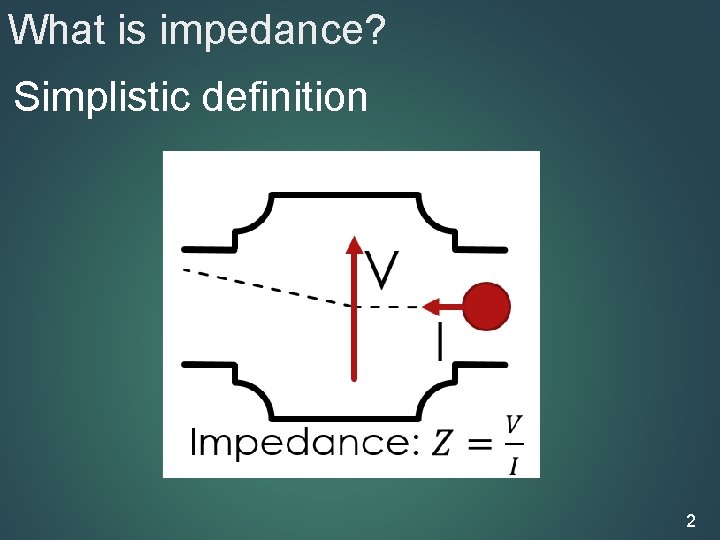
What is impedance? Simplistic definition 2

What is impedance? Actual definition Wake functions (time domain) In this presentation the beam is considered ultrarelativistic Impedance (frequency domain) Transverse driving (dipolar) and detuning (quadrupolar) impedances 3

Estimates of wall impedance • Fully analytical: explicit formulas for impedance • Semi-analytical: involves numerically finding integrals, roots, etc • Example: IW 2 D (field matching) • TLWall (transmission line theory) • Numerical: numerically solving for the fields with a mesh • BI 2 D • CST 4

An example of a fully-numerical calcuation BI 2 D implementation for the FCC-hh beamscreen GMSH (Geuzaine et al. ) triangular mesh Meshing the whole structure is required only for extremely low frequency! Otherwise: Surface Impedance Boundary Condition (SIBC) Uwe Niedermayer, TU Darmstadt 5

Field-matching method Following N. Mounet - “The LHC Transverse Coupled-Bunch Instability”, Ph. D thesis, 2012 6

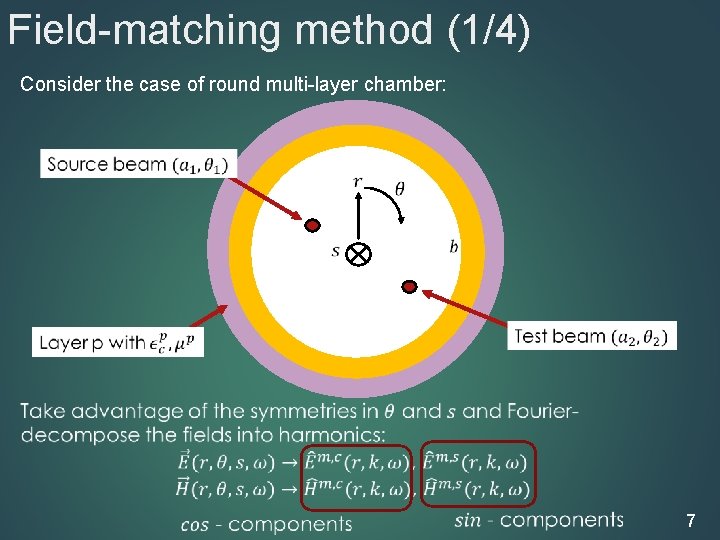
Field-matching method (1/4) Consider the case of round multi-layer chamber: 7

Field-matching method (2/4) Plug the Fourier-decomposed fields in Maxwell’s equations: Find the general solution for the longitudinal components in p-th layer: Modified Bessel functions Constants to find 8

Field-matching method (3/4) 9

Field-matching method (4/4) Finally, the solution is: Gives 0 -th order longitudinal impedance Gives detuning (quadrupolar) impedance Gives driving (dipolar) impedance Field matching code IW 2 D is available to use here: https: //twiki. cern. ch/twiki/bin/view/ABPComputing/Impedance. Wake 2 D 10

Analytical approach: surface impedance method 11

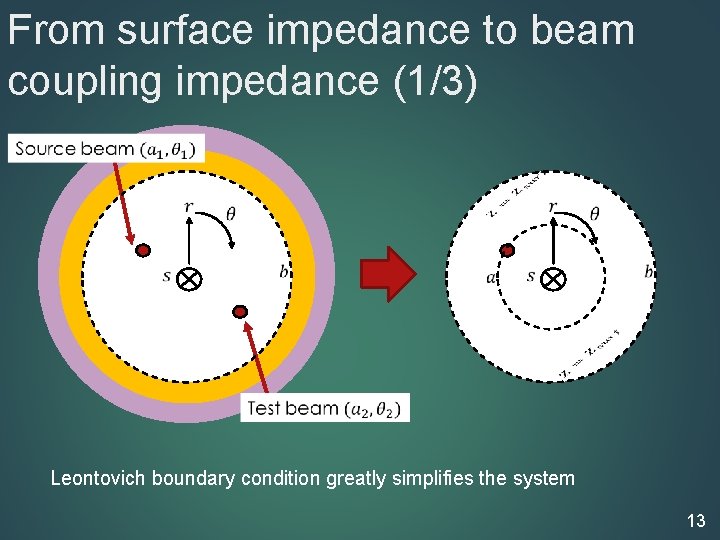
Surface impedance method beam Step 2: Relate the surface to the beam coupling impedance We will start with the second step 12

From surface impedance to beam coupling impedance (1/3) Leontovich boundary condition greatly simplifies the system 13

From surface impedance to beam coupling impedance (2/3) Following A. Chao - “Physics of collective beam instabilities in high energy accelerators”, we focus on the longitudinal and transverse beam coupling impedances 14

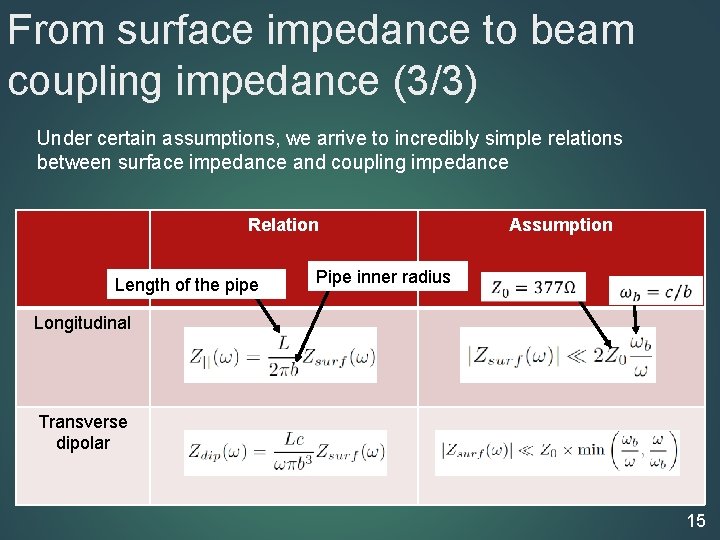
From surface impedance to beam coupling impedance (3/3) Under certain assumptions, we arrive to incredibly simple relations between surface impedance and coupling impedance Relation Length of the pipe Assumption Pipe inner radius Longitudinal Transverse dipolar 15

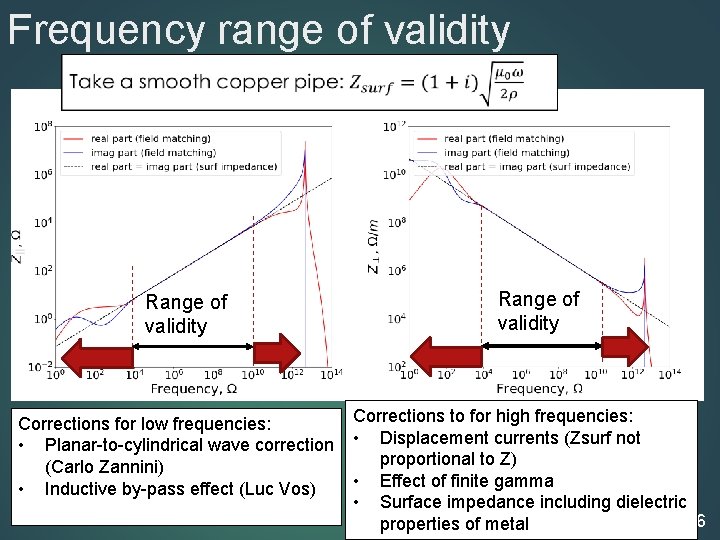
Frequency range of validity Range of validity Corrections for low frequencies: • Planar-to-cylindrical wave correction (Carlo Zannini) • Inductive by-pass effect (Luc Vos) Range of validity Corrections to for high frequencies: • Displacement currents (Zsurf not proportional to Z) • Effect of finite gamma • Surface impedance including dielectric 16 properties of metal

Analytical approach: surface impedance method two-layer model 17

Finding surface impedance: two-layer model vacuum layer bulk 18

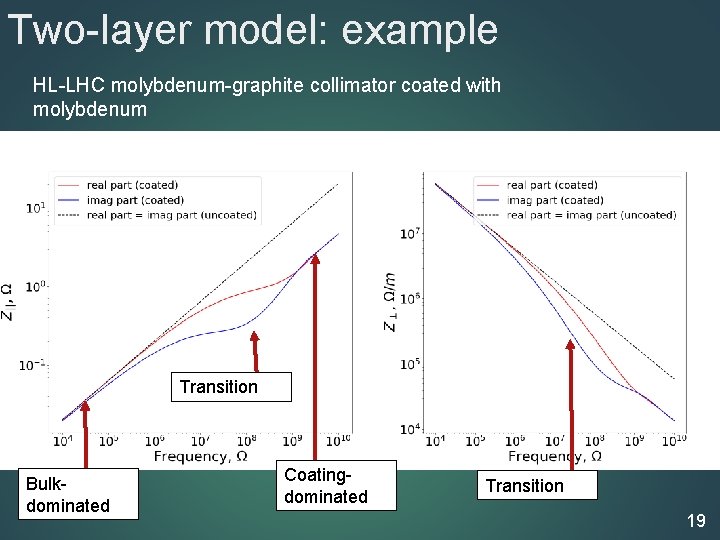
Two-layer model: example HL-LHC molybdenum-graphite collimator coated with molybdenum Transition Bulkdominated Coatingdominated Transition 19

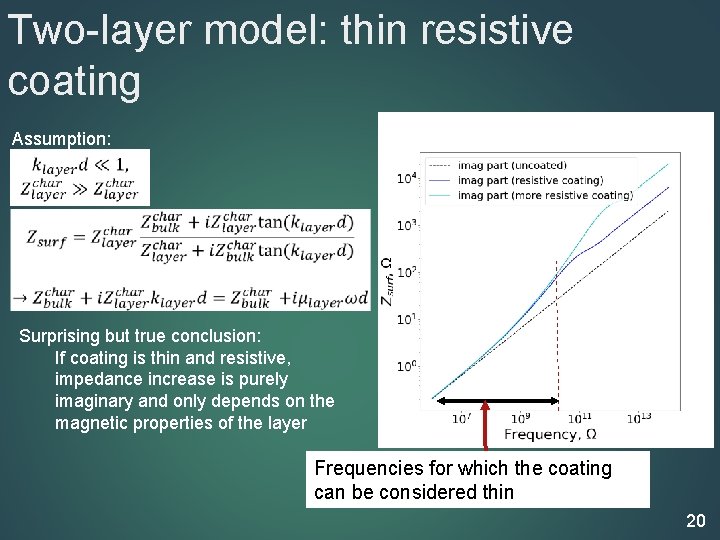
Two-layer model: thin resistive coating Assumption: Surprising but true conclusion: If coating is thin and resistive, impedance increase is purely imaginary and only depends on the magnetic properties of the layer Frequencies for which the coating can be considered thin 20

Analytical approach: surface impedance method linear conductivity model 21

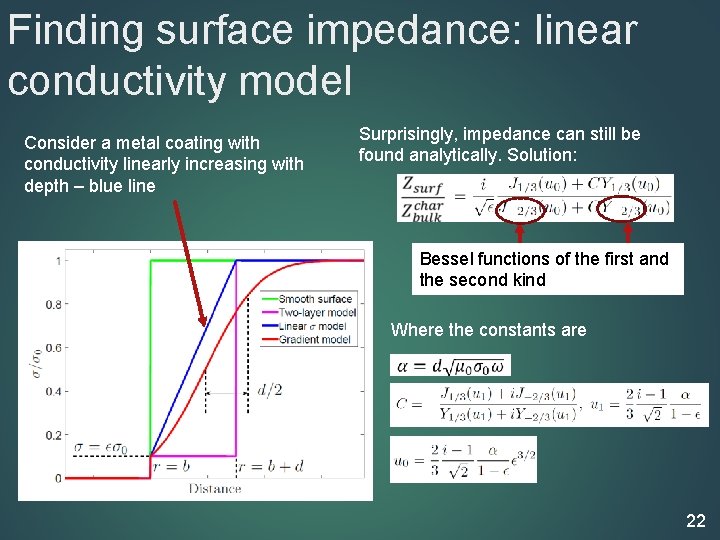
Finding surface impedance: linear conductivity model Consider a metal coating with conductivity linearly increasing with depth – blue line Surprisingly, impedance can still be found analytically. Solution: Bessel functions of the first and the second kind Where the constants are 22

Analytical approach: surface impedance method roughness models 23

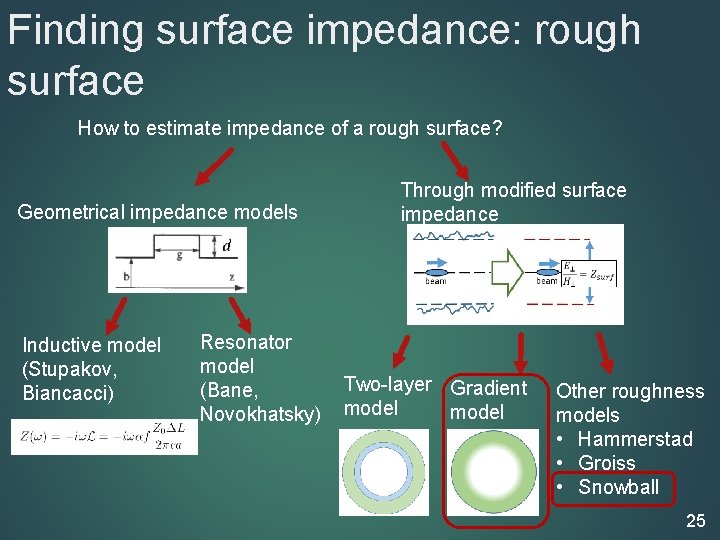
Finding surface impedance: rough surface 24

Finding surface impedance: rough surface How to estimate impedance of a rough surface? Geometrical impedance models Inductive model (Stupakov, Biancacci) Resonator model (Bane, Novokhatsky) Through modified surface impedance Two-layer Gradient model Other roughness models • Hammerstad • Groiss • Snowball 25

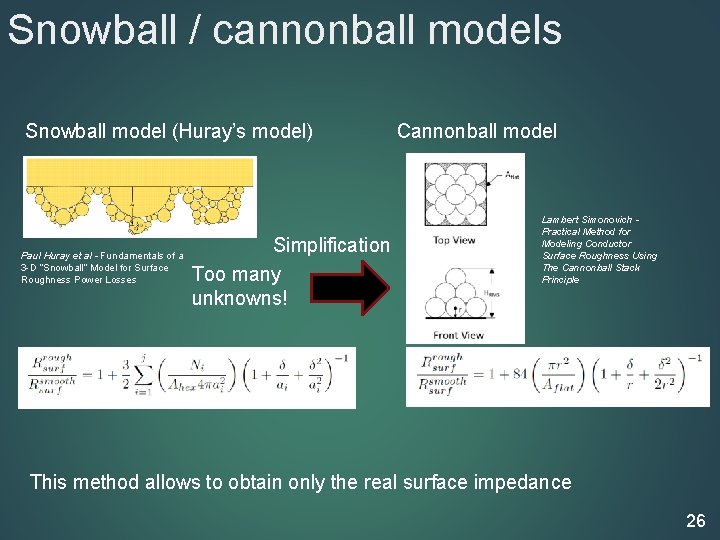
Snowball / cannonball models Snowball model (Huray’s model) Paul Huray et al - Fundamentals of a 3 -D “Snowball” Model for Surface Roughness Power Losses Simplification Too many unknowns! Cannonball model Lambert Simonovich Practical Method for Modeling Conductor Surface Roughness Using The Cannonball Stack Principle This method allows to obtain only the real surface impedance 26

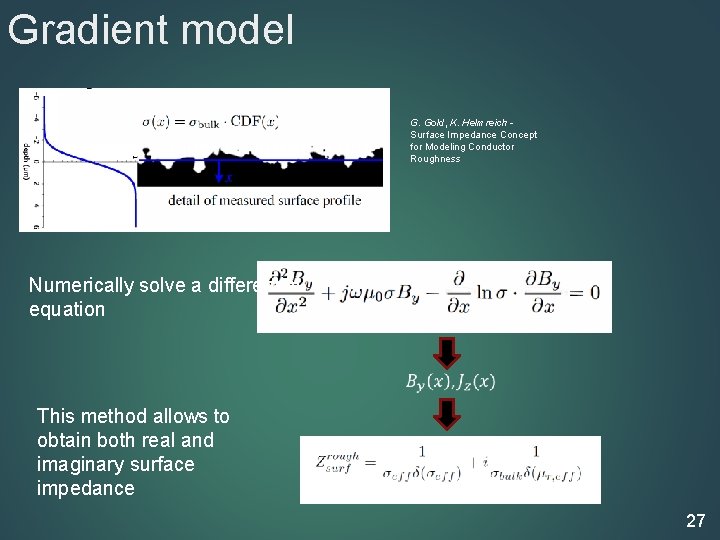
Gradient model G. Gold, K. Helmreich Surface Impedance Concept for Modeling Conductor Roughness Numerically solve a differential equation This method allows to obtain both real and imaginary surface impedance 27

Conclusions • Analytical models for coated surface impedance are a handy tool for a quick impedance estimate • Range of fully analytical model is limited (two-layer model, linear conductivity model) • Semi-analytical models that only simple computer calculations can tackle harder tasks: • Z at full frequency range with many layers (field matching, TLwall) • Rough surface impedance estimates with the gradient model 28

Back-up slides 29

From surface impedance to beam coupling impedance (3/3) Inductive bypass: L. Vos “The transverse impedance of a cylindrical pipe with arbitrary surface impedance” From Elias Métral, workshop "Beam Dynamics meets Vacuum, Collimation and Surfaces", Karlsruhe, Germany, 08 -10/03/2017 30