Analysis of Algorithms Analyzing Algorithms We need methods











![Recurrences-Example p MERGE-SORT(A[p. . r]) if p < r q= (p+r)/2 MERGE-SORT(A[p. . q]) Recurrences-Example p MERGE-SORT(A[p. . r]) if p < r q= (p+r)/2 MERGE-SORT(A[p. . q])](https://slidetodoc.com/presentation_image_h2/618e7bc84a9c67c1731774a2a8e21c33/image-15.jpg)







![T(n)=a. T(n/b)+f(n) [CLRS] Fig 4. 4 T(n)=a. T(n/b)+f(n) [CLRS] Fig 4. 4](https://slidetodoc.com/presentation_image_h2/618e7bc84a9c67c1731774a2a8e21c33/image-25.jpg)



![Math review See also: [CLRS] – Appendix A - Summation formulas Math review See also: [CLRS] – Appendix A - Summation formulas](https://slidetodoc.com/presentation_image_h2/618e7bc84a9c67c1731774a2a8e21c33/image-29.jpg)
![Applying the math review See also: [CLRS] – Appendix A - Summation formulas Applying the math review See also: [CLRS] – Appendix A - Summation formulas](https://slidetodoc.com/presentation_image_h2/618e7bc84a9c67c1731774a2a8e21c33/image-30.jpg)
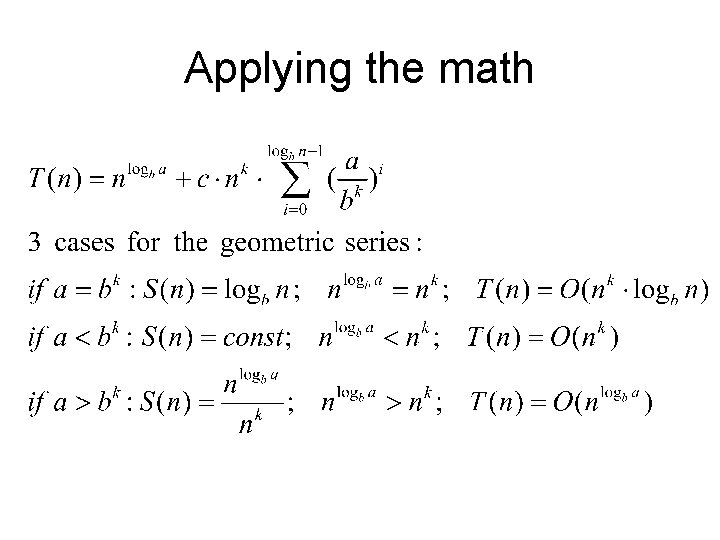












![Bibliography • Review Analysis of algorithms: – [CLRS] – chap 3 (Growth of functions), Bibliography • Review Analysis of algorithms: – [CLRS] – chap 3 (Growth of functions),](https://slidetodoc.com/presentation_image_h2/618e7bc84a9c67c1731774a2a8e21c33/image-44.jpg)

- Slides: 45

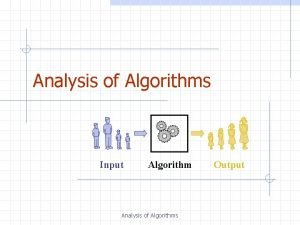
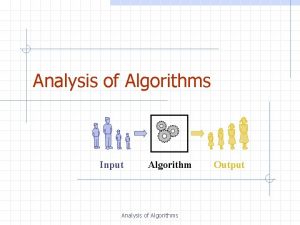
Analysis of Algorithms

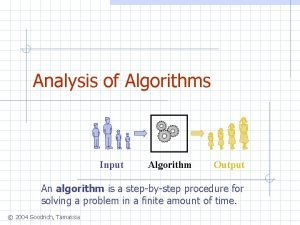
Analyzing Algorithms • We need methods and metrics to analyze algorithms for: – Correctness • Methods for proving correctness – Efficiency • Time complexity, Asymptotic analysis

Lecture Outline • Short Review on Asymptotic Analysis – Asymptotic notations • Upper bound, Lower bound, Tight bound – Running time estimation in complex cases: • Summations • Recurrences – The substitution method – The recursion tree method – The Master Theorem

Review - Asymptotic Analysis • Running time depends on the size of the input – T(n): the time taken on input with size n – it is the rate of growth, or order of growth, of the running time that really interests us – Look at growth of T(n) as n→∞. • Worst-case and average-case running times are difficult to compute precisely, so we calculate upper and lower bounds of the function.

Review - Asymptotic Notations • O: Big-Oh = asymptotic upper bound • Ω: Big-Omega = asymptotic lower bound • Θ: Theta = asymptotically tight bound [CLRS] – chap 3

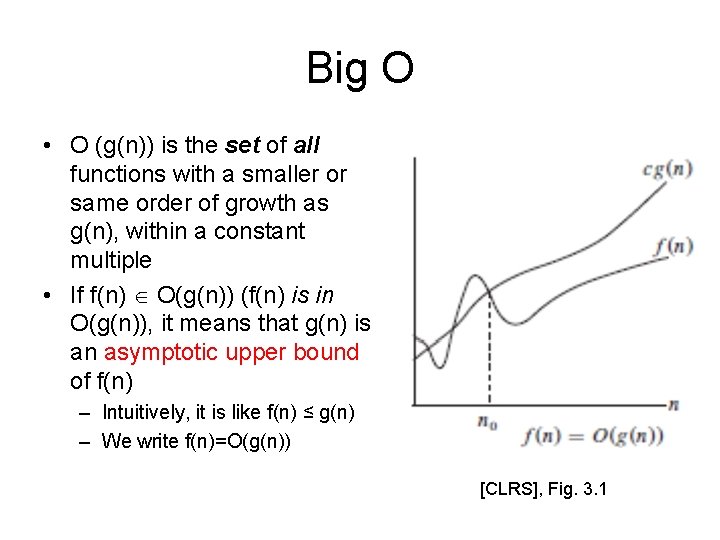
Big O • O (g(n)) is the set of all functions with a smaller or same order of growth as g(n), within a constant multiple • If f(n) O(g(n)) (f(n) is in O(g(n)), it means that g(n) is an asymptotic upper bound of f(n) – Intuitively, it is like f(n) ≤ g(n) – We write f(n)=O(g(n)) [CLRS], Fig. 3. 1

Examples • Examples: – if g(n)=n 2 , some functions f(n) in O(n 2) are:

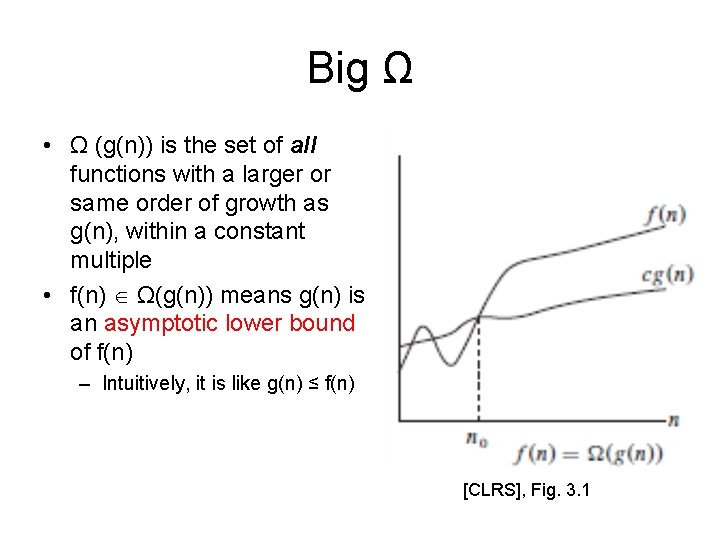
Big Ω • Ω (g(n)) is the set of all functions with a larger or same order of growth as g(n), within a constant multiple • f(n) Ω(g(n)) means g(n) is an asymptotic lower bound of f(n) – Intuitively, it is like g(n) ≤ f(n) [CLRS], Fig. 3. 1

Examples • Examples: – if g(n)=n 2 , some functions f(n) in Ω (n 2):

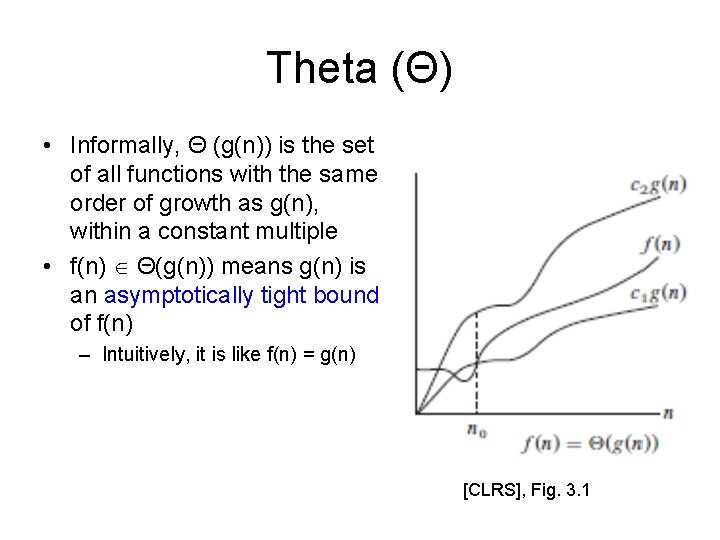
Theta (Θ) • Informally, Θ (g(n)) is the set of all functions with the same order of growth as g(n), within a constant multiple • f(n) Θ(g(n)) means g(n) is an asymptotically tight bound of f(n) – Intuitively, it is like f(n) = g(n) [CLRS], Fig. 3. 1

Examples • Examples of functions f(n) in Θ(n 2): • f(n) is in Θ(g(n)) if both f(n) is in O(g(n)) and f(n) is in Ω(g(n))

Running Time Estimation • In practice, estimating the running time T(n) means finding a function f(n), such that T(n) in O(f(n)) or T(n) in Θ(f(n)) • If we prove that T(n) in O(f(n)) we just guarantee that T(n) “is not worse than f(n)” – Attention to overapproximations ! • If we prove that T(n) is in Θ(f(n)) we actually determine the order of growth of the running time.

Running Time Estimation • Simplifying assumption: – each statement takes the same unit amount of time. – usually we can assume that the statements within a loop will be executed as many times as the maximum permitted by the loop control. • More complex situations when running time estimation can be difficult: – Summations (a loop is executed many times, each time with a different complexity) – Recurrences (recursive algorithms)

Summations - Example For i=1 to n do For j=1 to i do For k=1 to i do something_simple n i<=n O(n 3) O(1) But what about Θ ? Function something_simple is executed exactly S(n) times: S(n)= Σi=1 n i 2 = n(n+1)(2 n+1)/6 S(n) in Θ(n 3) See also: [CLRS] – Appendix A - Summation formulas
![RecurrencesExample p MERGESORTAp r if p r q pr2 MERGESORTAp q Recurrences-Example p MERGE-SORT(A[p. . r]) if p < r q= (p+r)/2 MERGE-SORT(A[p. . q])](https://slidetodoc.com/presentation_image_h2/618e7bc84a9c67c1731774a2a8e21c33/image-15.jpg)
Recurrences-Example p MERGE-SORT(A[p. . r]) if p < r q= (p+r)/2 MERGE-SORT(A[p. . q]) MERGE-SORT(A[q+1. . r]) MERGE(A[p. . r], q) q To sort an array of n numbers, call MERGE-SORT(A[1. . n]) T(n) = Θ(1), n=1 2*T(n/2) + Θ(n), n>1 In case of recursive algorithms, we get a recurrence relationship on the run time function T(n) r

Solving Recurrences • The recurrence has to be solved in order to find out T(n) as a function of n • General methods for solving recurrences: – Substitution Method – Recursion-tree Method

The Substitution Method • The substitution method for solving recurrences: – do a few substitution steps in the recurrence relationship until you can guess the solution (the formula) and prove it with math induction • Example: applying the substitution method for solving the Merge. Sort recurrence

Substitution meth: T(n)=2 *T(n/2)+n T(n) = 2*T(n/2)+n T(n/2)=2*T(n/22)+n/2 By substituting T(n/2) in the first relationship, we obtain: T(n) = 22*T(n/22)+2*n/2+n = 22*T(n/22)+2*n T(n/22) = 2*T(n/23)+n/22 T(n) = 23*T(n/23)+22*n/22+2*n = 23*T(n/23)+3*n. . T(n) = 2 k*T(n/2 k)+k*n (we assume) T(n/2 k) = 2*T(n/2 k+1)+n/2 k (we know by the recurrence formula) By substituting T(n/2 k+1) in the relationship above, we obtain: T(n)=2 k+1*T(n/2 k+1)+(k+1)*n => assumption proved T(n) = 2 k*T(n/2 k)+k*n. How many steps k=x are needed to eliminate the recurence ? When n/2 x=1 => x=log 2 n T(n)=n * T(1) + n * log 2 n Θ(n * log 2 n)

The Recursion Tree Method • The recursion tree method for solving recurrences: – converts the recurrence into a tree of the recursive function calls. – Each node has a cost, representing the workload of the corresponding call (without the recursive calls done there). The total workload results by adding the workloads of all nodes. It uses techniques for bounding summations. • Example: applying the recursion tree method for solving the Merge. Sort recurrence

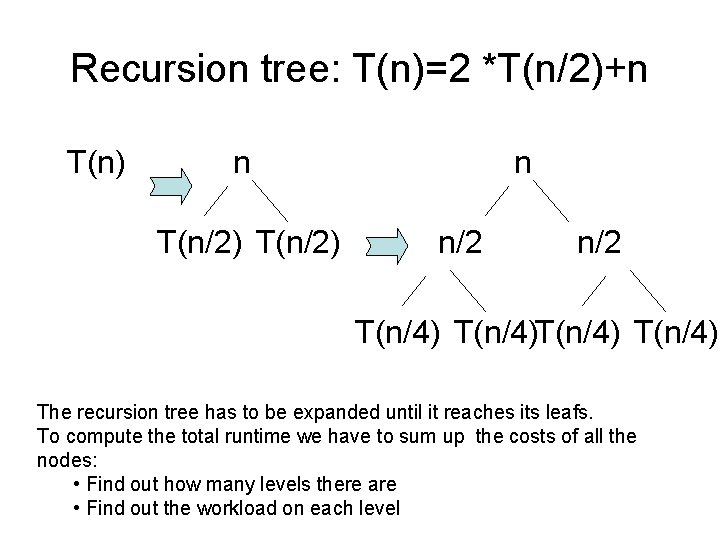
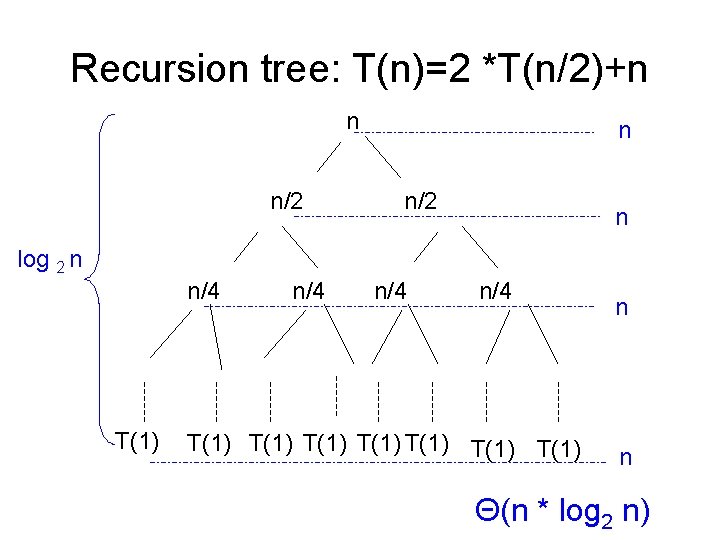
Recursion tree: T(n)=2 *T(n/2)+n T(n) n T(n/2) n n/2 T(n/4)T(n/4) The recursion tree has to be expanded until it reaches its leafs. To compute the total runtime we have to sum up the costs of all the nodes: • Find out how many levels there are • Find out the workload on each level

Recursion tree: T(n)=2 *T(n/2)+n n n/2 n log 2 n n/4 T(1) n/4 n/4 T(1) T(1) n n Θ(n * log 2 n)

Solving Recurrences • A particular case are the recurrences of the form T(n)=a. T(n/b)+f(n), f(n)=c*nk – this form of recurrence appears frequently in divideand-conquer algorithms • The Master Theorem: provides bounds for recurrences of this particular form – 3 cases, according to the values of a, b and k – Can be proved by substitution or recursion-tree • [CLRS] chap 4

T(n)=a. T(n/b)+f(n) Recursion tree

T(n)=a. T(n/b)+f(n) • Which is the height of the tree ? • How many nodes are there on each level ? • How many leaves are there ? • Which is the workload on each non-leaf level ? • Which is the workload on the leaves level ? Recursion tree
![Tna Tnbfn CLRS Fig 4 4 T(n)=a. T(n/b)+f(n) [CLRS] Fig 4. 4](https://slidetodoc.com/presentation_image_h2/618e7bc84a9c67c1731774a2a8e21c33/image-25.jpg)
T(n)=a. T(n/b)+f(n) [CLRS] Fig 4. 4

T(n)=a. T(n/b)+f(n) Intuitively: T(n) will result good if: b is big a is small f(n)=O(nk), k is small [CLRS] Fig 4. 4

T(n)=a. T(n/b)+f(n) From the recursion tree: Workload in leaves Sum for all levels Workload per level i

T(n)=a. T(n/b)+f(n), f(n)=c*nk Geometric series of factor a/bk
![Math review See also CLRS Appendix A Summation formulas Math review See also: [CLRS] – Appendix A - Summation formulas](https://slidetodoc.com/presentation_image_h2/618e7bc84a9c67c1731774a2a8e21c33/image-29.jpg)
Math review See also: [CLRS] – Appendix A - Summation formulas
![Applying the math review See also CLRS Appendix A Summation formulas Applying the math review See also: [CLRS] – Appendix A - Summation formulas](https://slidetodoc.com/presentation_image_h2/618e7bc84a9c67c1731774a2a8e21c33/image-30.jpg)
Applying the math review See also: [CLRS] – Appendix A - Summation formulas
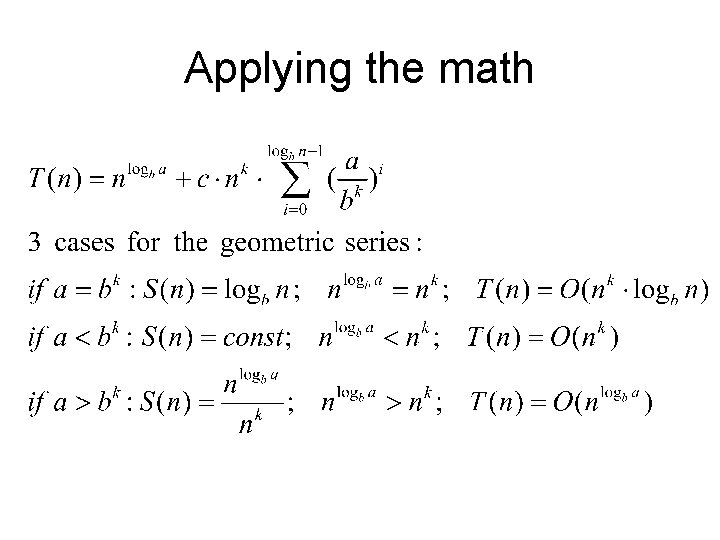
Applying the math

T(n)=a. T(n/b)+f(n), f(n)=c*nk We just proved the Master Theorem: The solution of the recurrence relation is:

Merge-sort revisited T(n) = Θ(1), n=1 2*T(n/2) + Θ(n), n>1 • The recurrence relation of Merge-sort is a case of the master theorem, for a=2, b=2, k=1 • Case a=bk => Θ(nk * log n), k=1 => Θ(n * log n) • Conclusion: In order to solve a recurrence having the form T(n)=a. T(n/b)+f(n), f(n)=c*nk, we can either: – Memorize the result of the Master Theorem and apply it directly – Do the reasoning (by substitution or by recursion-tree) on the particular case

Master Theorem – Applicability • The results of theorem are valid ONLY for particular cases of recurrences, these of the form T(n)=a. T(n/b)+f(n), f(n)=c*nk • For all other types of recurrences, you have to apply the substitution method or the recursion tree method – Examples: recursive factorial, recursive Fibonacci – the Master theorem does NOT apply for this kind of recurrences !

Difficult recurrences • Some recurrences can be difficult to solve mathematically, thus we cannot directly determine a tight bound (Theta) for their running times. • In this cases, we can apply one of the following strategies: – Strategy 1: Try to determine a lower bound (Omega) and an upper bound (O). – Stragtegy 2: Guess a function for the tight bound and prove that it verifies the recurrence formula (The “Guess and prove” approach)

Example: Recursive Fibonacci function Fibonacci (n: integer) returns integer is: if (n==1) or (n==2) return 1 else return Fibonacci (n-1) + Fibonacci (n-2) T(n) = c 1, n<=2 T(n-1) + T(n-2) + c 2, n>2 This recurrence is difficult to solve by substitution or call tree. We have to try something else.

Example: Computing Lower and upper bounds • We always should try to do our best: – find a lower bound which is the highest lower bound that we can prove, and – find an upper bound which is the lowest upper bound that we can prove. • If we can prove the same function both for lower bound and upper bound, then we even managed to find the tight bound (Theta).

Example: Upper bound for Fibonacci T(n) = c 1, n<=2 T(n-1) + T(n-2) + c 2, n>2 T(n) is in O(f(n)), if there exist a>0, n 0>0, such that T(n)<=a*f(n), for all n>=n 0. For any algorithm, we have: T(n-2)<=T(n-1) Taking this into account (replacing T(n-2) with the bigger T(n -1)), the Fibonacci recurrence leads to: T(n)=T(n-1)+T(n-2)+c 2 <= 2*T(n-1) + c 2

Example: Upper bound for Fibonacci (cont) T(n)=T(n-1)+T(n-2)+c 2 <= 2*T(n-1) + c 2 By substitution, T(n)<= 2^k *T(n-k) + c 2 (2^(k-1) + 2^(k-2) +. . + 2^2 +2 +1) Substitution stops when n-k=1, k=n-1 Results that T(n)<= a* 2^n T(n) is in O(2^n)

Example: Lower bound for Fibonacci T(n) = c 1, n<=2 T(n-1) + T(n-2) + c 2, n>2 T(n) is in Omega(f(n)), if there exist b>0, n 0>0, such that T(n)>=b*f(n), for all n>=n 0. For any algorithm, we have: T(n-2)<=T(n-1), T(n-3)<=T(n-2), . . . T(n-k)<=T(n-k+1) Taking this into account, replacing T(n-1) by the smaller T(n -2), the Fibonacci recurrence leads to: T(n)=T(n-1)+T(n-2)+c 2 >= 2*T(n-2) + c 2

Example: Lower bound for Fibonacci (cont) T(n)=T(n-1)+T(n-2)+c 2 >= 2*T(n-2) + c 2 By substitution, T(n)>= 2^k *T(n-2*k) + c 2 ( 2^(k-1)) +. . + 2^2 +2 +1) Substitution stops when k=n/2 Results that: T(n)>= b* 2^(n/2) T(n) is in Omega(2^n/2)

Example: Guess and prove By upper and lower bounds we found that Fibonacci time is: b* 2^(n/2) <=T(n) <= a* 2^n We presume that T(n)=x^n. We have to prove this (to find the value of x) T(n)=T(n-1)+T(n-2)+c 2 x^n = x^(n-1)+ x^(n-2) x^2 – x-1 = 0 => x=1. 618 Fibonacci is Θ (x^n)

Conclusions • We estimate asymptotic complexity with: Upper Bound (Big-O), Lower Bound (Big-Omega) and Tight Bound (Big-Theta). • Determining the asymptotic complexity of recursive algorithms can be difficult. For this, you will have to solve the recurrence relationship that describes the recursive algorithm. • General methods for solving recurrence relationships are the substitution method and the recursion-tree method. For certain particular types of recurrences (the divide-and-conquer type of recurrences) the result is also given by the Master Theorem. • Sometimes solving certain recurrence relationships is mathematically difficult and we cannot calculate the tight bound. In this case we can apply one of the following methods: – introduce approximations, that will help us determine only lower bounds and upper bounds – guess and prove
![Bibliography Review Analysis of algorithms CLRS chap 3 Growth of functions Bibliography • Review Analysis of algorithms: – [CLRS] – chap 3 (Growth of functions),](https://slidetodoc.com/presentation_image_h2/618e7bc84a9c67c1731774a2a8e21c33/image-44.jpg)
Bibliography • Review Analysis of algorithms: – [CLRS] – chap 3 (Growth of functions), chap 4 (Recurrences, Master Theorem) or – [Manber] – chap 3

And there is more to this subject … • The running time can vary also depending on the input values, not only input size: • Average vs. Worst-case. Worst case =running time of a program is guaranteed less than a certain bound (as a function of the input size), no matter what the input. This approach is needed in critical software. In other applications it is enough to analyse average performance. This may need probabilistic analysis. • Randomized algorithms. Random inputs guide the behaviour, in the hope of achieving good performance in the "average case“. Their running time and/or their output are random variables. [CLRS ch 5] • Amortized analysis: provides a worst-case performance guarantee on a sequence of operations; while each operation may have its worst case guarantee, a specific sequence of these operations may behave better than the individuals. [CLRS ch 17]. Will have a small example later at disjoint sets.
 Direct wax pattern
Direct wax pattern Design and analysis of algorithms syllabus
Design and analysis of algorithms syllabus Algorithm analysis examples
Algorithm analysis examples Analysis of algorithms
Analysis of algorithms Association analysis: basic concepts and algorithms
Association analysis: basic concepts and algorithms Algorithmic input output
Algorithmic input output Analysis of algorithms
Analysis of algorithms Analysis of algorithms
Analysis of algorithms Steps in mathematical analysis of non recursive algorithm
Steps in mathematical analysis of non recursive algorithm Cluster analysis: basic concepts and algorithms
Cluster analysis: basic concepts and algorithms Randomized algorithms and probabilistic analysis
Randomized algorithms and probabilistic analysis Design and analysis of algorithms introduction
Design and analysis of algorithms introduction Analysis of algorithms lecture notes
Analysis of algorithms lecture notes Cluster analysis basic concepts and algorithms
Cluster analysis basic concepts and algorithms Cjih
Cjih Goals of analysis of algorithms
Goals of analysis of algorithms Cluster analysis basic concepts and algorithms
Cluster analysis basic concepts and algorithms Binary search in design and analysis of algorithms
Binary search in design and analysis of algorithms Introduction to the design and analysis of algorithms
Introduction to the design and analysis of algorithms Competitive analysis algorithms
Competitive analysis algorithms Design and analysis of algorithms
Design and analysis of algorithms Design and analysis of algorithms
Design and analysis of algorithms Cluster analysis basic concepts and algorithms
Cluster analysis basic concepts and algorithms Comp 482
Comp 482 Tna adalah
Tna adalah Types of needs analysis in esp
Types of needs analysis in esp Contoh training need assessment
Contoh training need assessment Human resources training and development
Human resources training and development Pedagogy analysis
Pedagogy analysis What is fact finding in system analysis and design
What is fact finding in system analysis and design Virtual work method truss
Virtual work method truss Feedback analysis methods
Feedback analysis methods Legal data analysis
Legal data analysis Data analysis methods
Data analysis methods Methods of job analysis in industrial psychology
Methods of job analysis in industrial psychology Difference between occlusion and mixed-crystal formation
Difference between occlusion and mixed-crystal formation Factor analysis
Factor analysis Define amortized analysis
Define amortized analysis What is input output design
What is input output design Vendor rating
Vendor rating Titrimetric analysis
Titrimetric analysis Method of characterization
Method of characterization Factors to consider in evaluating retail trading area
Factors to consider in evaluating retail trading area Methods of vibration analysis
Methods of vibration analysis Research methods design and analysis
Research methods design and analysis Cei writing
Cei writing