Analog Communications Dr M Venu Gopala Rao A

Analog Communications Dr. M. Venu Gopala Rao A. M. I. E. T. E, M. Tech, Ph. D(Engg) Cert. in R. S. T ( City & Guild’s London Institute, London) F. I. E. T. E, L. M. I. S. T. E, I. S. O. I. , S. S. I. , M. I. A. E. Professor, Dept. of ECE, K L University mvgr 03@kluniversity. in

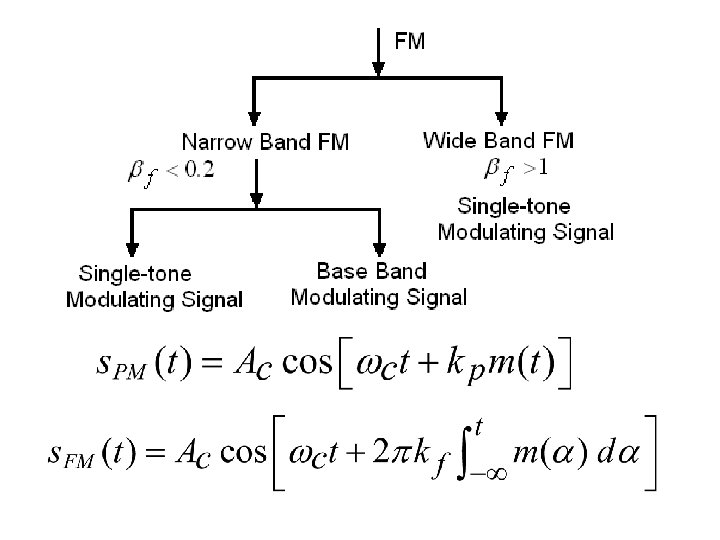
Wideband FM

Single-tone Wideband FM an even, periodic function an odd periodic function where Jn(βf) is a Bessel function of the first kind of n th order with argument βf.

Wideband FM…

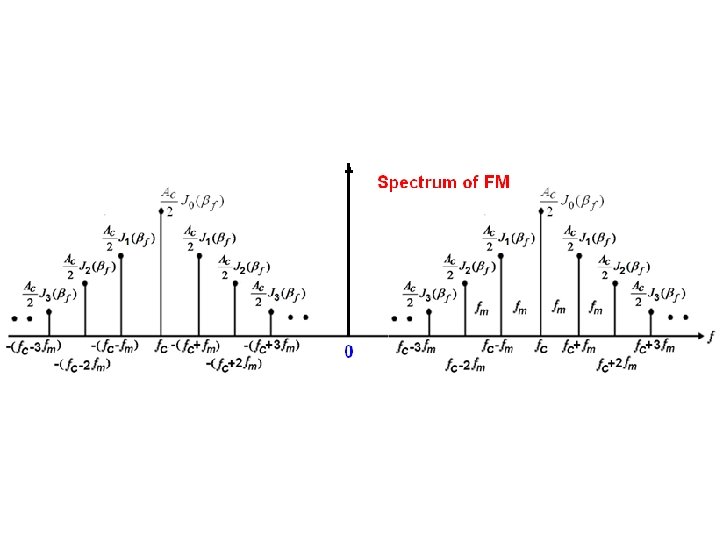
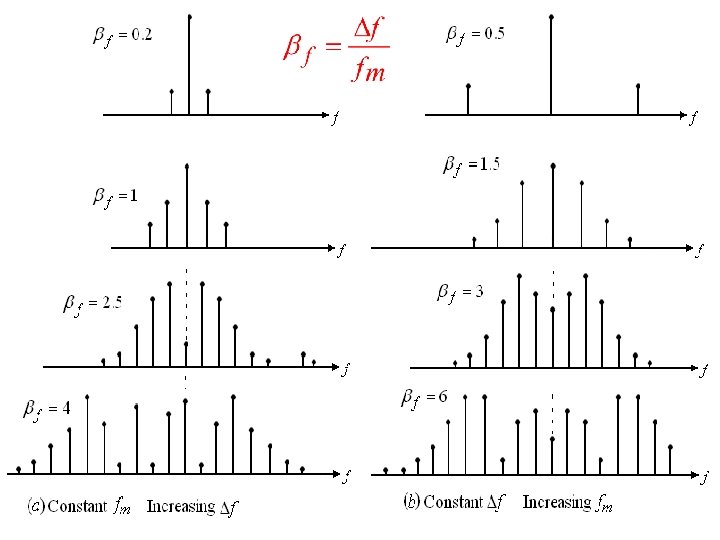
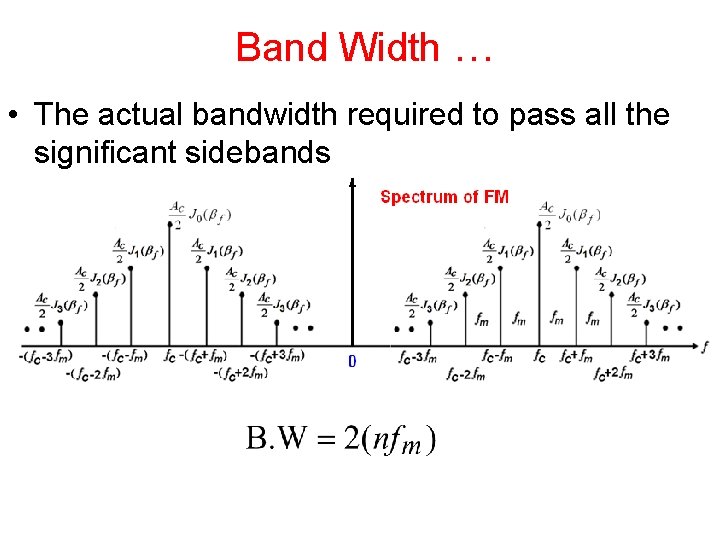
Spectrum of WBFM The carrier with amplitude A set of side frequencies specified simultaneously on the either side of the carrier at a frequency separation of

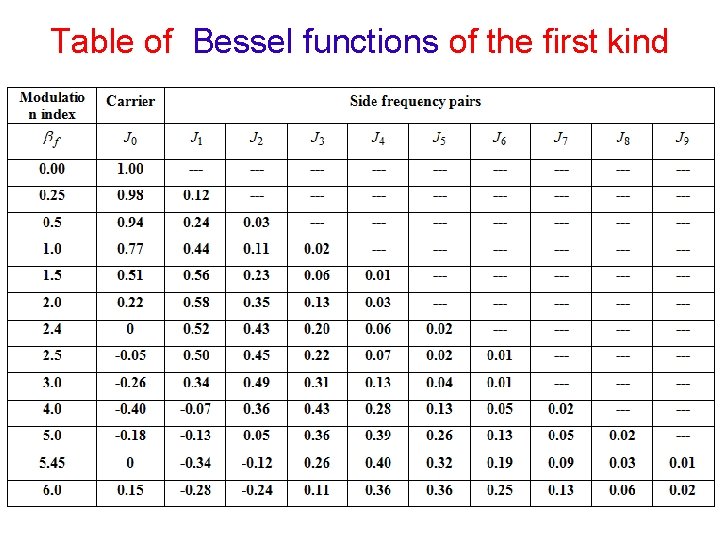
Table of Bessel functions of the first kind

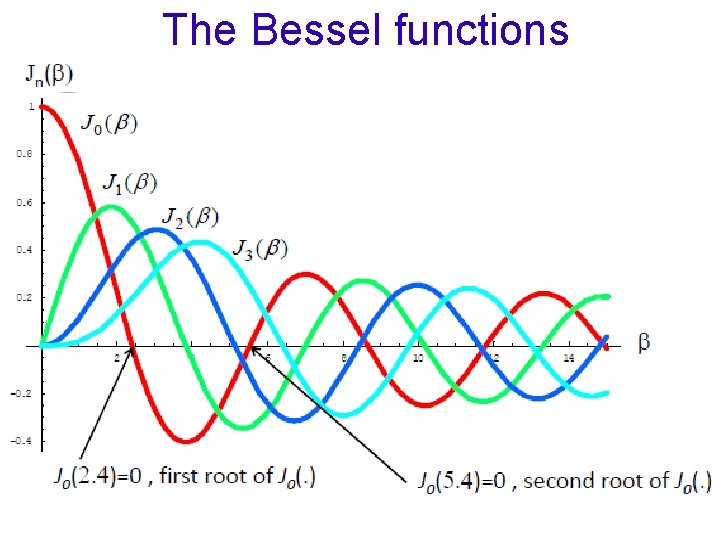
The Bessel functions

Observations Ø In AM: Carrier and first two sidebands. In WBFM: Carrier and infinite number of sidebands. Ø The J coefficients represent the amplitude of a particular pair of sidebands. Ø Thus the modulation index determine the number of sideband components have significant amplitudes. Ø No. of sidebands increases Ø In AM but in FM as , Total power is constant, but

Observations… Ø In AM, the BW = 2 fm , but in FM the BW is determined by fm and f Ø In FM, the amplitude of the carrier component is constant, where as in AM, the carrier component does not remains constant. The J coefficients J 0 is a function of f. The overall amplitude of the FM wave remains constant. Ø The carrier component of the FM wave disappear completely at f = 2. 4, 5. 5, 8. 6, 11. 8 etc. First carrier null, second carrier null. . .

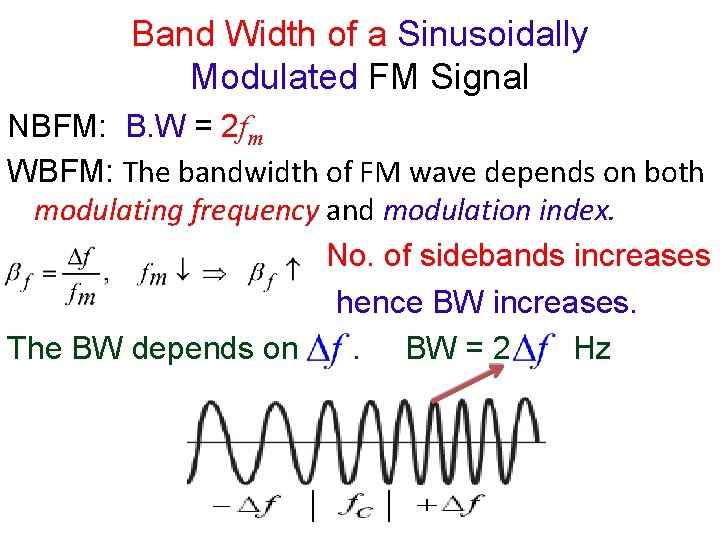
Band Width of a Sinusoidally Modulated FM Signal NBFM: B. W = 2 fm WBFM: The bandwidth of FM wave depends on both modulating frequency and modulation index. No. of sidebands increases hence BW increases. The BW depends on. BW = 2 Hz

Band Width … • The actual bandwidth required to pass all the significant sidebands

Carson’s Rule The Carson rule state that the approximate bandwidth necessary to transmit an angle modulated wave as twice the sum of the frequency deviation and the highest modulating signal frequency. Approximates the 98% of total power. Carson’s BW is less than actual Tx BW

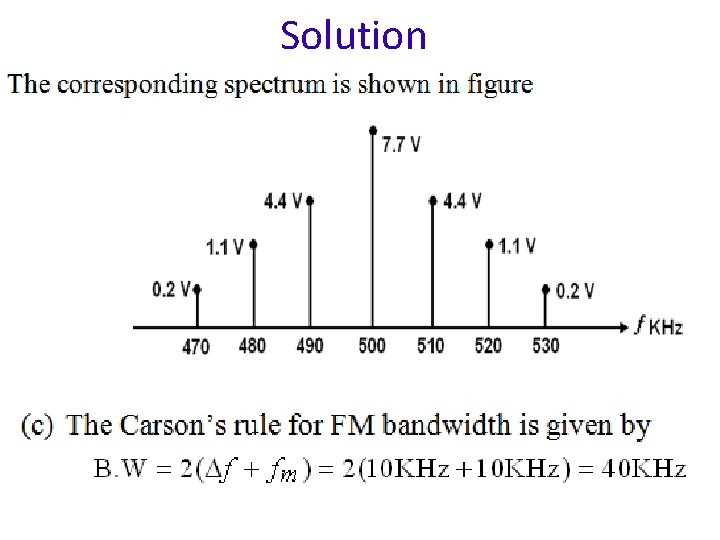
Example For an FM modulator with peak frequency deviation 10 KHz, a modulating signal frequency 10 KHz, peak modulating signal amplitude 10 V, and a 500 KHz carrier, determine a) Actual minimum bandwidth from the Bessel table. b) Plot the output frequency spectrum for the Bessel approximation. c) Approximation minimum bandwidth using Carson’s rule. d) Comment the results. • From the Bessel table for

Solution

Solution

Solution (d) Comments: The bandwidth from Carson’s rule is less than the actual minimum bandwidth required to pass all the significant sideband sets as defined by the Bessel table. Therefore a system that was design using Carson’s rule would have a narrower bandwidth and their poor performance than a system designed using the Bessel table. For modulation indices above 5, Carson’s rule is a close approximation to the actual bandwidth required.

Effect of the Modulation Index on Bandwidth The Carson’s rule

Deviation Ratio • For a given FM system, the minimum bandwidth is greatest when the maximum frequency deviation is obtained with the maximum signal frequency (i. e. , the highest modulating frequency occurs with the maximum amplitude allowed).

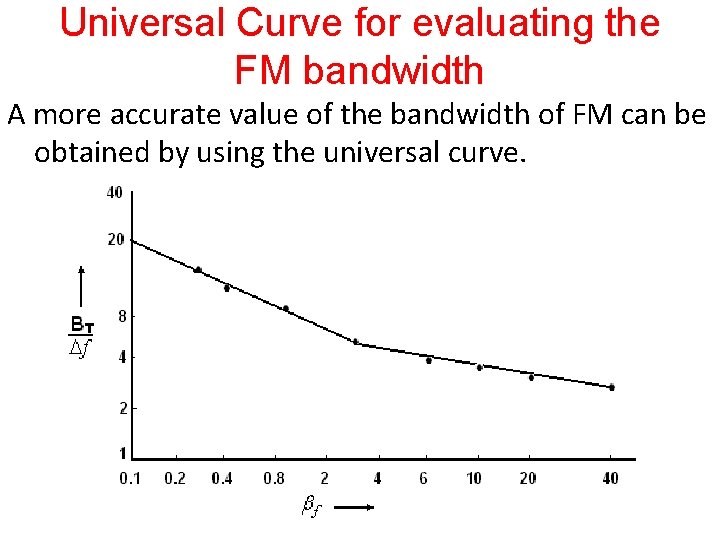
Universal Curve for evaluating the FM bandwidth A more accurate value of the bandwidth of FM can be obtained by using the universal curve.

Average Power of an Angle Modulated Wave

End WBFM