AMDM Unit 7 Graphs and Graph Terminology Structure

Graphs consist of § points called vertices § lines called edges 1. Edges connect

Graphs are a structure for describing relationships between objects. (The vertices denote the objects

In this graph, the vertices represent people’s names. Such a graph could represent friendships

Graph Terminology o tw e r a s e c ti r e V

Graph Terminology e th d r a w to e ic tw A loop

Example 3: 1) Find the degree of each vertex. A D 2) Is A

Graph Terminology f o e c n e u q e s a is

Graph Terminology t a s d n e d n a ts r ta

Graph Terminology a f o s t r a p d e t c

Example 4: 1) Find a path from B to K passing through W but

Graph Terminology t a th th a p a is th a P r

Example: The graph on the left has no Euler paths, but the on the

Königsberg’s Bridges II (The rare sequel that is not entirely gratuitous. ) This is

What Euler realized was that most of the information on the maps had no

Example The Kevin Bacon Game (http: //www. cs. virginia. edu/oracle/)

Euler’s Theorems Euler’s Theorem 1 (a) If a graph has any odd vertices, then

Euler’s Theorem 2 (a) If a graph has more than two odd vertices, then

Königsburg’s Bridges Let us consider again the Königsburg Brdige puzzle as represented by the

Euler’s Theorem 3 (a) The sum of the degrees of all the vertices of

A quick summary. . . Number of odd vertices Conclusion 0 Graph has Euler

Slides: 23

Download presentation

AMDM Unit 7 Graphs and Graph Terminology Structure of networks & graphs

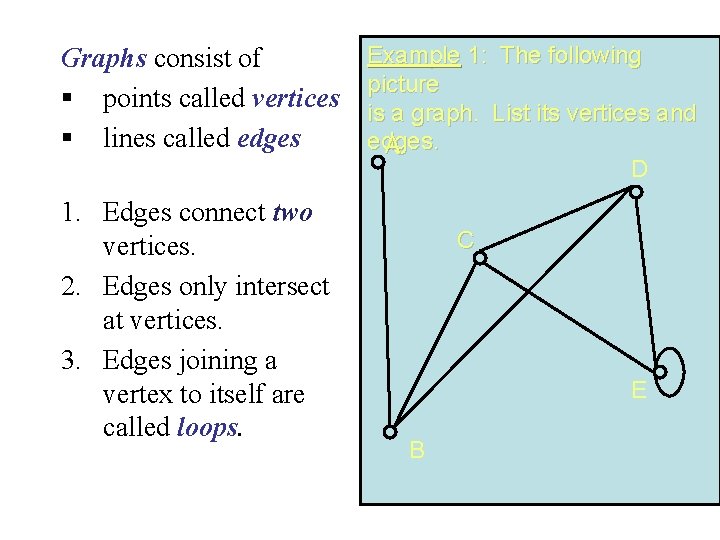
Graphs consist of § points called vertices § lines called edges 1. Edges connect two vertices. 2. Edges only intersect at vertices. 3. Edges joining a vertex to itself are called loops. Example 1: The following picture is a graph. List its vertices and edges. A D C E B

Graphs are a structure for describing relationships between objects. (The vertices denote the objects and the edges represent the relationship. )

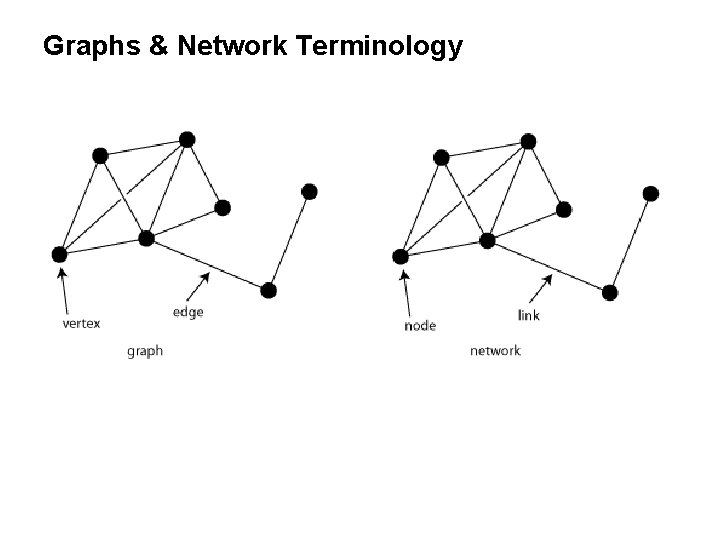
Graphs & Network Terminology

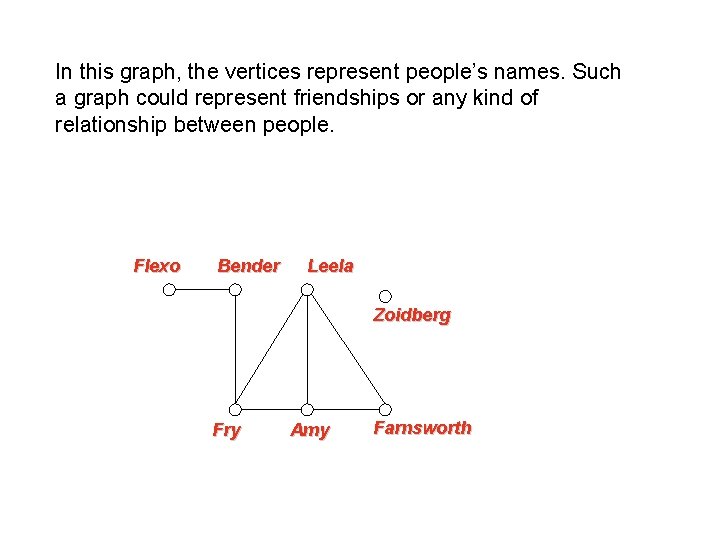
In this graph, the vertices represent people’s names. Such a graph could represent friendships or any kind of relationship between people. Flexo Bender Leela Zoidberg Fry Amy Farnsworth

Graph Terminology o tw e r a s e c ti r e V t n e c Adja n a y b d e in jo e r a th s vertice edge. s e g d e o tw e r a s e Adjacent Edg. x te r e v a t c e s r te that in e th is x te r e v a f o e e r The deg. x te r e v t a th t a s e g d number of e

Graph Terminology e th d r a w to e ic tw A loop counts degree. f o x te r e v a is x te r e v An odd degree. f o x te r e v a is x te r An even ve even degree.

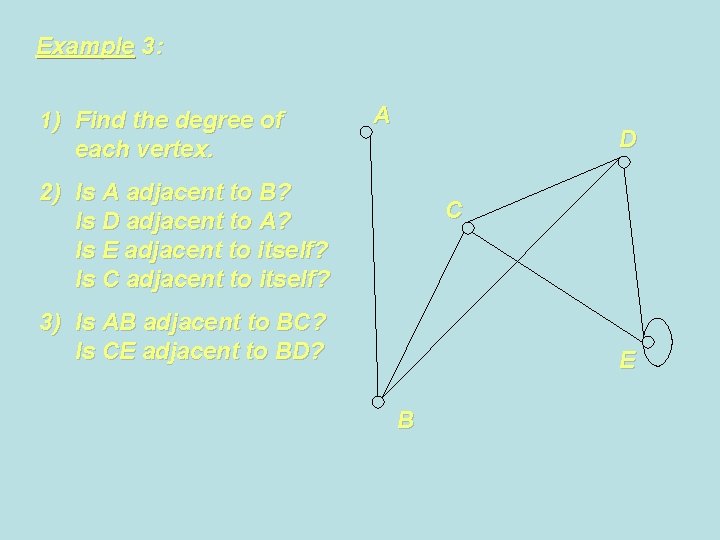
Example 3: 1) Find the degree of each vertex. A D 2) Is A adjacent to B? Is D adjacent to A? Is E adjacent to itself? Is C adjacent to itself? C 3) Is AB adjacent to BC? Is CE adjacent to BD? E B

Graph Terminology f o e c n e u q e s a is th A pa x te r e v h c a e t a th h c u s vertices a In t. x e n e th to t n e c is adja e b n a c e g d e h c a e , path th g n le e h T. e c n o traveled only f o r e b m u n e th is th a of a p edges in that path.

Graph Terminology t a s d n e d n a ts r ta s A path that a d e ll a c is x te r e v the same circuit. y n a if d te c e n n o c A graph is y b d e in jo e b n a c s e c two verti le ib s s o p t o n is is th If. a path then the graph is disconnected.

Graph Terminology a f o s t r a p d e t c e The conn e r a h p a r g d e t c e disconn. s t n e n o p m o c d e ll a c a in e g d e n a is e g A brid e s o h w h p a r g d e t c e conn removal makes it disconnected.

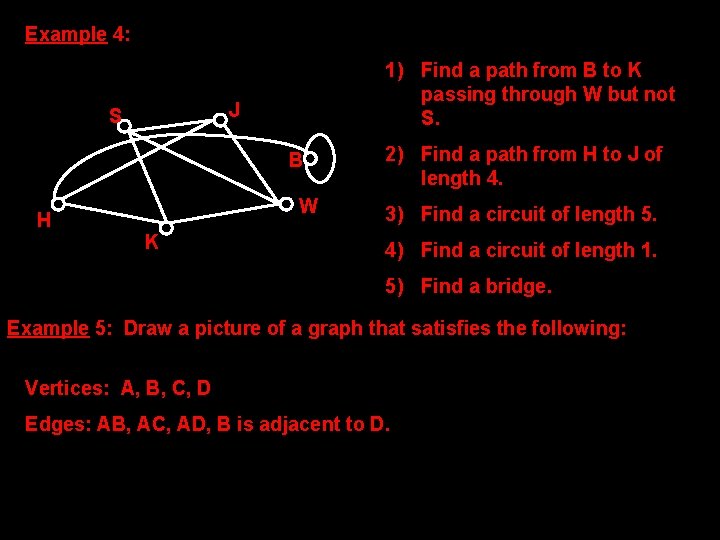
Example 4: 1) Find a path from B to K passing through W but not S. J S B H W K 2) Find a path from H to J of length 4. 3) Find a circuit of length 5. 4) Find a circuit of length 1. 5) Find a bridge. Example 5: Draw a picture of a graph that satisfies the following: Vertices: A, B, C, D Edges: AB, AC, AD, B is adjacent to D.

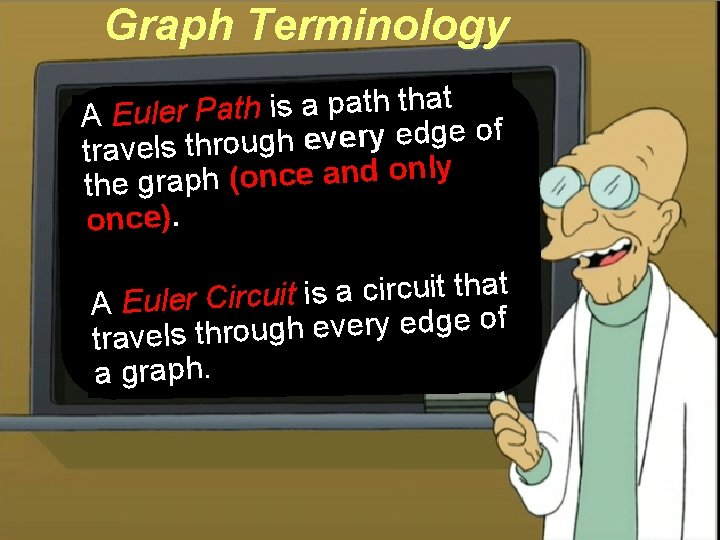
Graph Terminology t a th th a p a is th a P r le A Eu f o e g d e y r e v e h g u o r travels th ly n o d n a e c n o ( h p a the gr once). t a th it u c ir c a is it u c ir A Euler C f o e g d e y r e v e h g u o r travels th a graph.

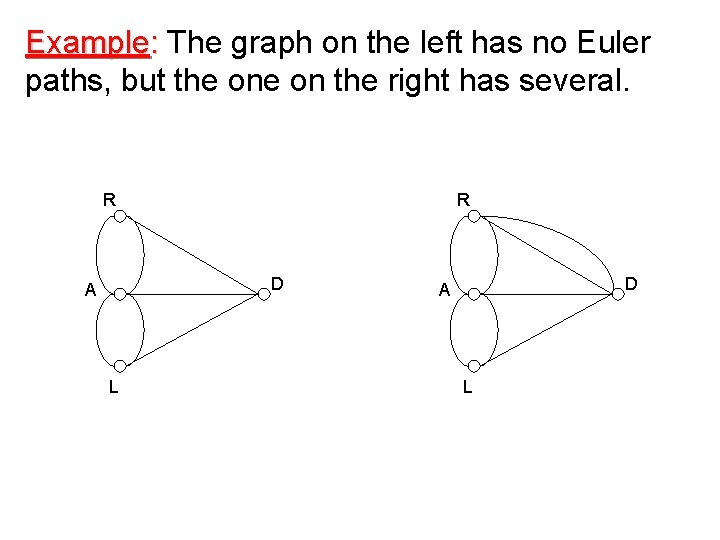
Example: The graph on the left has no Euler paths, but the on the right has several. R R D A L

Graph Models and Euler’s Theorems

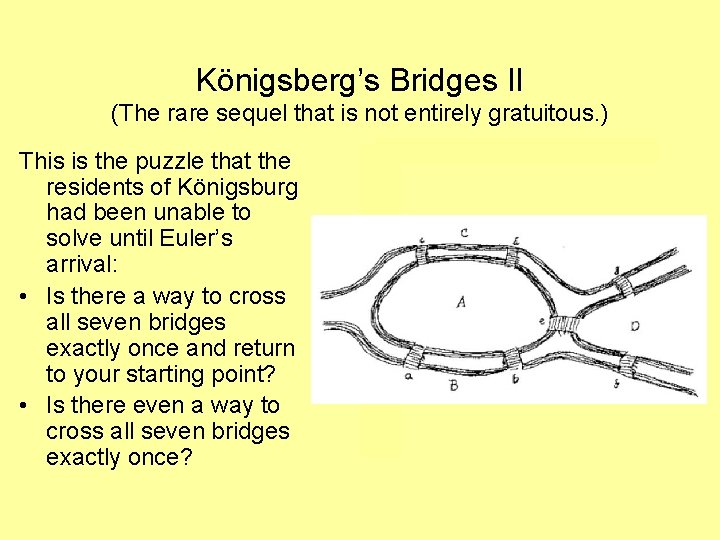
Königsberg’s Bridges II (The rare sequel that is not entirely gratuitous. ) This is the puzzle that the residents of Königsburg had been unable to solve until Euler’s arrival: • Is there a way to cross all seven bridges exactly once and return to your starting point? • Is there even a way to cross all seven bridges exactly once?

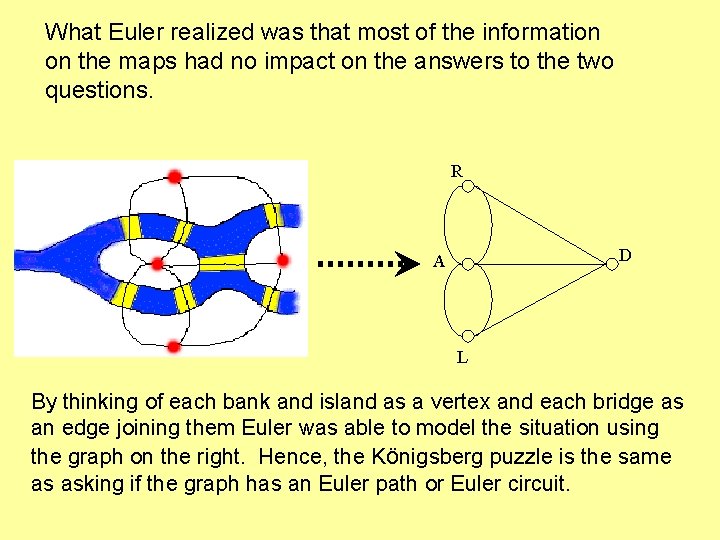
What Euler realized was that most of the information on the maps had no impact on the answers to the two questions. R D A L By thinking of each bank and island as a vertex and each bridge as an edge joining them Euler was able to model the situation using the graph on the right. Hence, the Königsberg puzzle is the same as asking if the graph has an Euler path or Euler circuit.

Example The Kevin Bacon Game (http: //www. cs. virginia. edu/oracle/)

Euler’s Theorems Euler’s Theorem 1 (a) If a graph has any odd vertices, then it cannot have an Euler circuit. (b) If a graph is connected and every vertex is even, then it has at least one Euler circuit.

Euler’s Theorem 2 (a) If a graph has more than two odd vertices, then it cannot have an Euler path. (b) If a connected graph has exactly two odd vertices then it has at least one Euler path starting at one odd vertex and ending at another odd vertex.

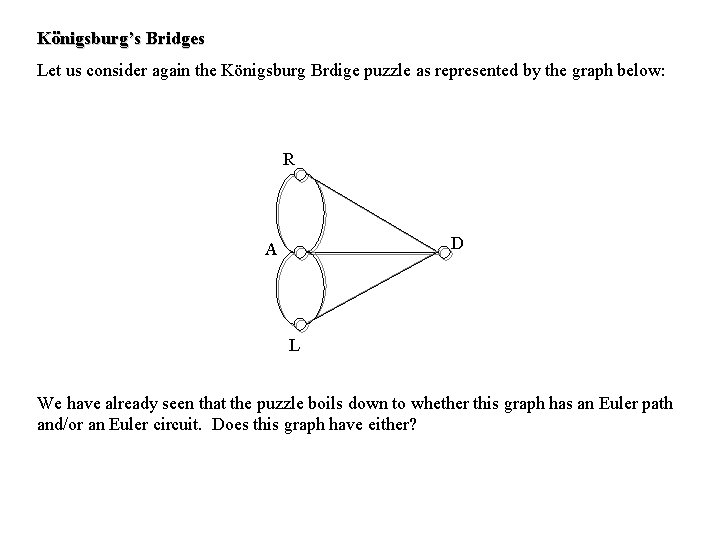
Königsburg’s Bridges Let us consider again the Königsburg Brdige puzzle as represented by the graph below: R D A L We have already seen that the puzzle boils down to whether this graph has an Euler path and/or an Euler circuit. Does this graph have either?

Euler’s Theorem 3 (a) The sum of the degrees of all the vertices of a graph equals twice the number of edges. (b) A graph always has an even number of odd vertices.

A quick summary. . . Number of odd vertices Conclusion 0 Graph has Euler circuit(s) 2 Graph has Euler path(s) but no Euler circuit Graph has no Euler path and no Euler circuit Impossible! 4, 6, 8, . . . 1, 3, 5, . . .