Graphs and Infinite Loops Graphs Terminology Edges Vertices

Graphs and Infinite Loops

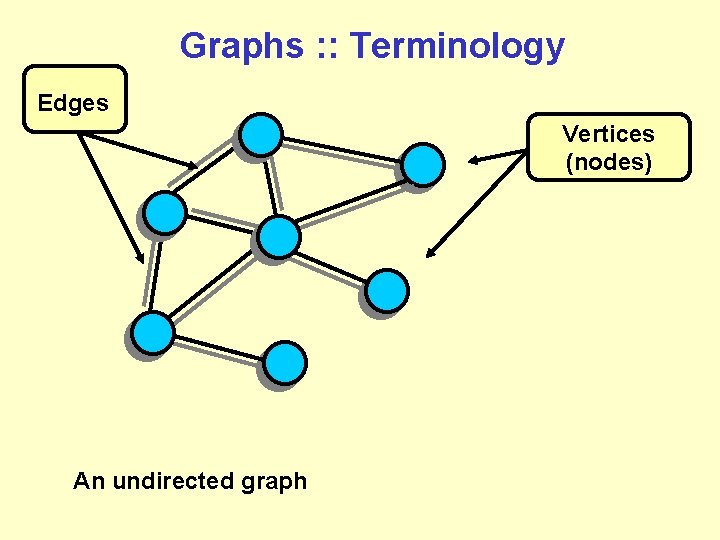
Graphs : : Terminology Edges Vertices (nodes) An undirected graph

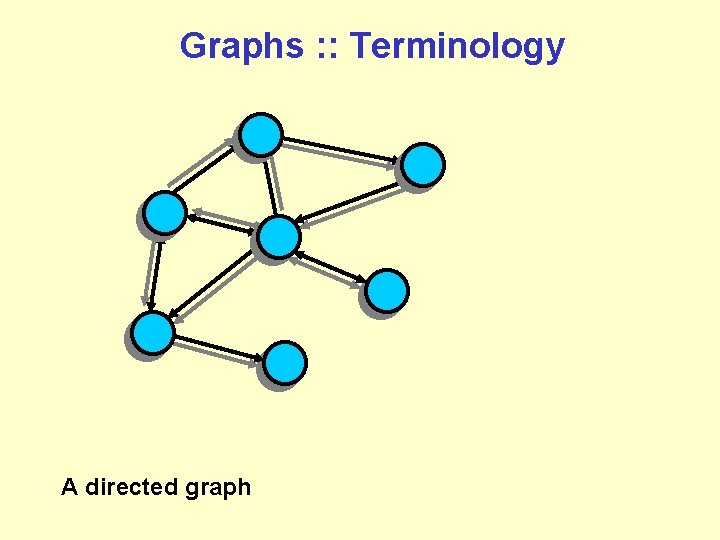
Graphs : : Terminology A directed graph

Internally… 3 1 2 Node 1 edges Node 2 edges Node 1 Node 3 edges Node 2 Node 4 edges Node 2 Node 3 Node 4 4

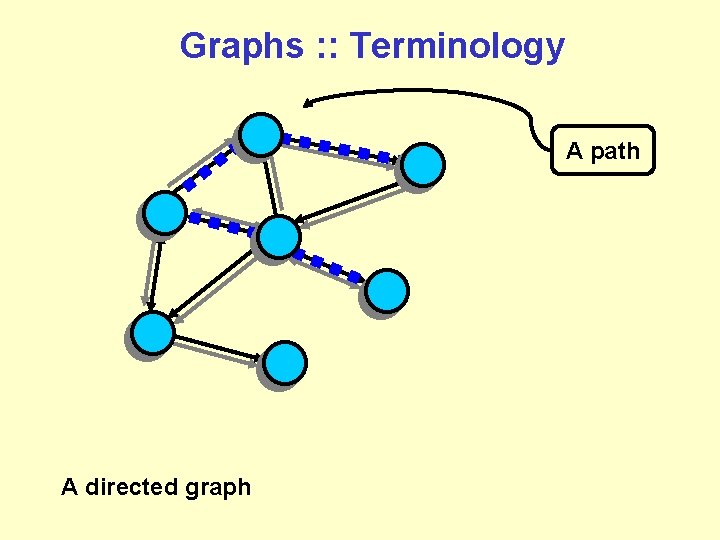
Graphs : : Terminology A path A directed graph

public class Node { private String cityname; private Linked. List<Node> gets. To; boolean has. Route(Node to) { if (this. equals(to)) return true; else { for (Node c : this. gets. To) { if (c. has. Route(to)) { return true; } } return false; } } }

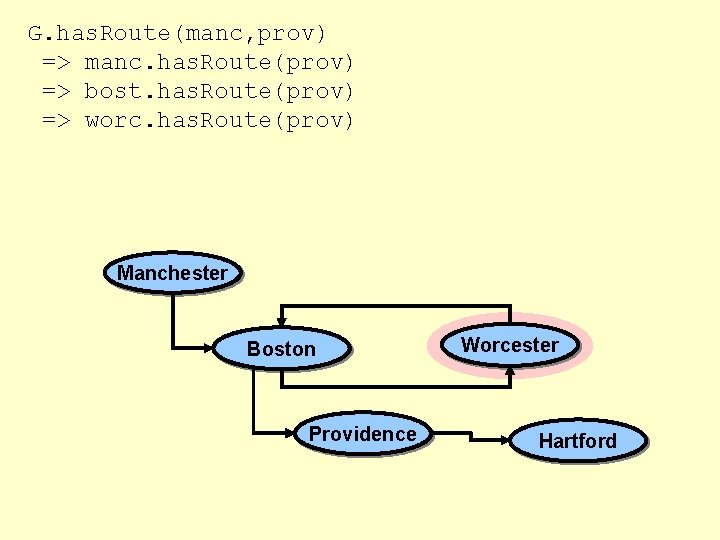
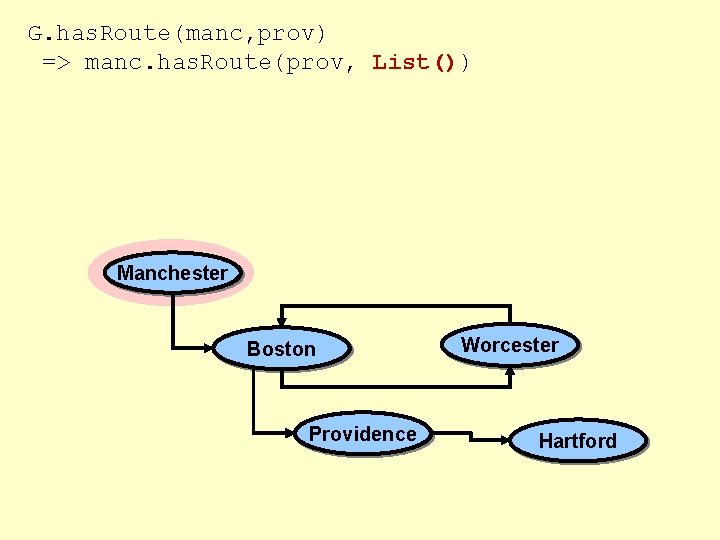
G. has. Route(manc, prov) => manc. has. Route(prov) Manchester Boston Providence Worcester Hartford

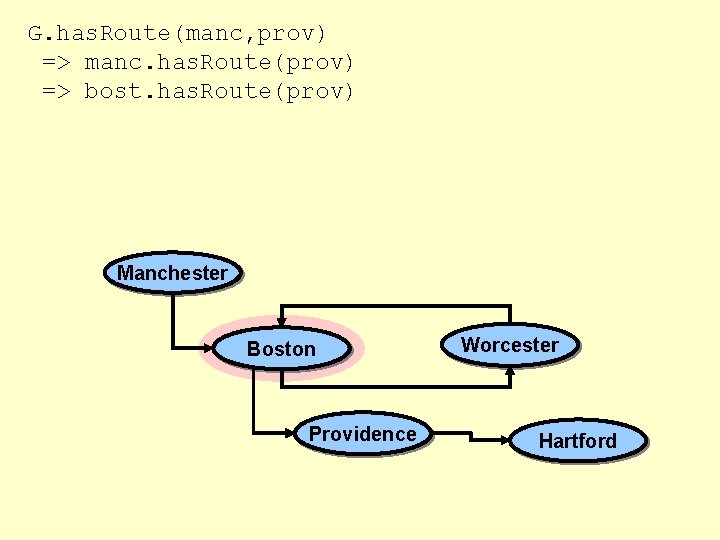
G. has. Route(manc, prov) => manc. has. Route(prov) => bost. has. Route(prov) Manchester Boston Providence Worcester Hartford

G. has. Route(manc, prov) => manc. has. Route(prov) => bost. has. Route(prov) => worc. has. Route(prov) Manchester Boston Providence Worcester Hartford

G. has. Route(manc, prov) => manc. has. Route(prov) => bost. has. Route(prov) => worc. has. Route(prov) => bost. has. Route(prov) Manchester Boston Providence Worcester Hartford

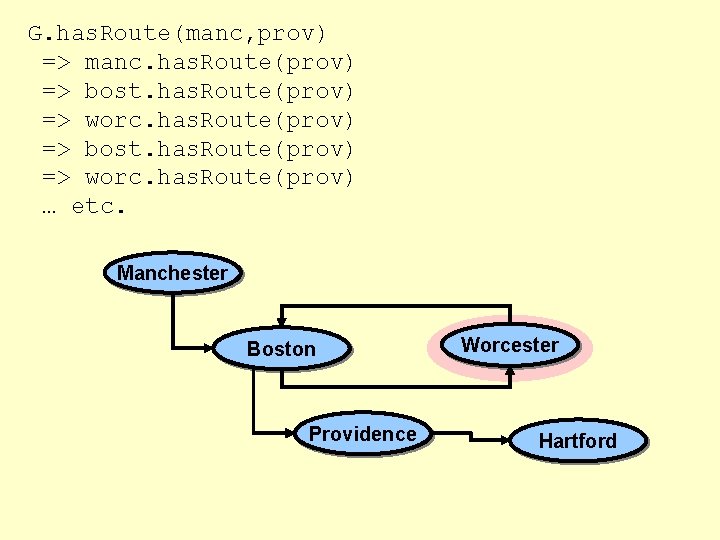
G. has. Route(manc, prov) => manc. has. Route(prov) => bost. has. Route(prov) => worc. has. Route(prov) … etc. Manchester Boston Providence Worcester Hartford

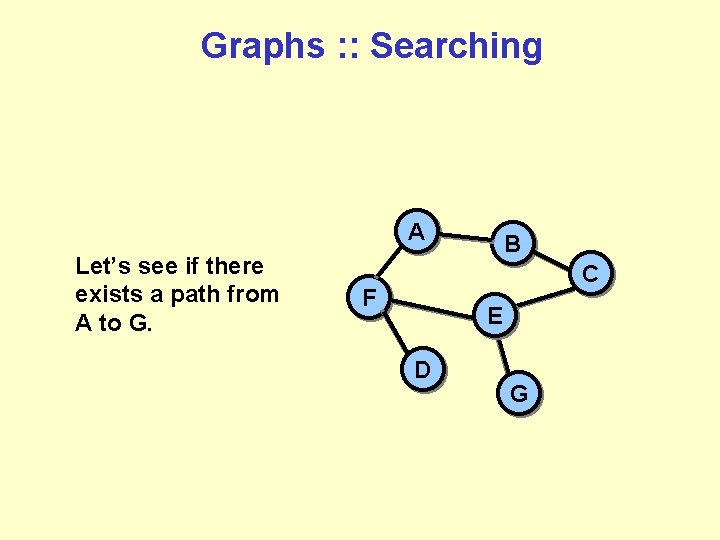
Graphs : : Searching A Let’s see if there exists a path from A to G. B C F E D G

Graphs : : Searching A C F E D Current Node A B G

Graphs : : Searching A C F E D Current Node A Adjacencies F B B G

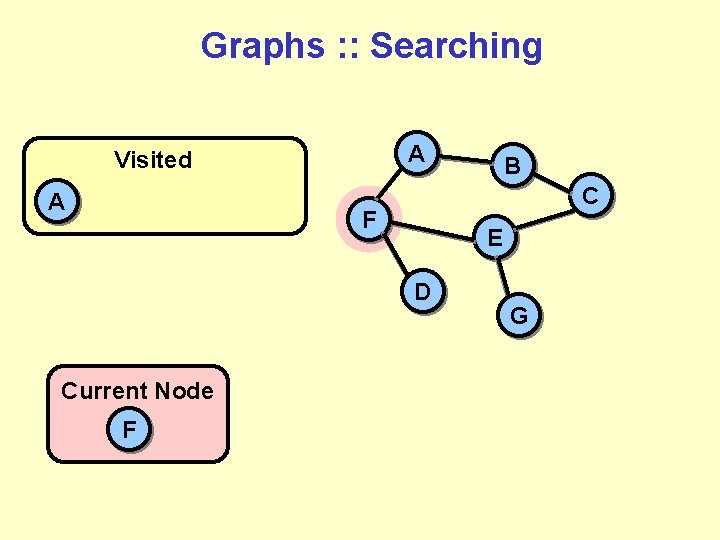
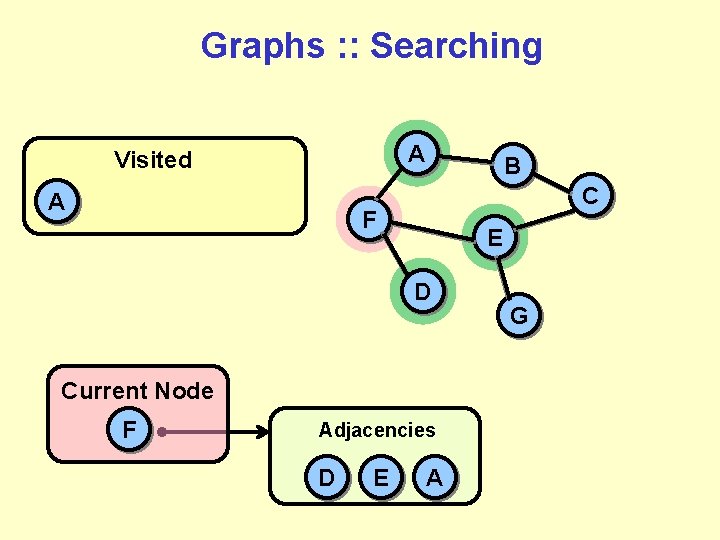
Graphs : : Searching A Visited A C F E D Current Node F B G

Graphs : : Searching A Visited A B C F E D Current Node F Adjacencies D E A G

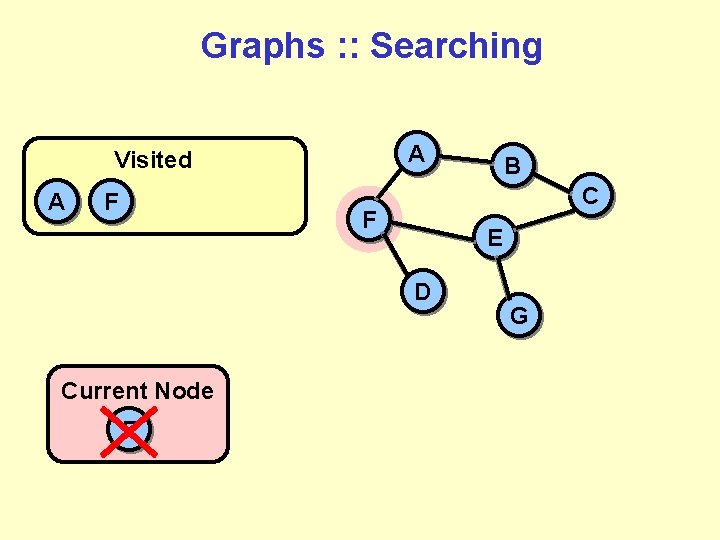
Graphs : : Searching A Visited A B C F E D Current Node F Adjacencies D F E B A G BUT WAIT! We already visited node A.

Graphs : : Searching A Visited A F C F E D Current Node F B G

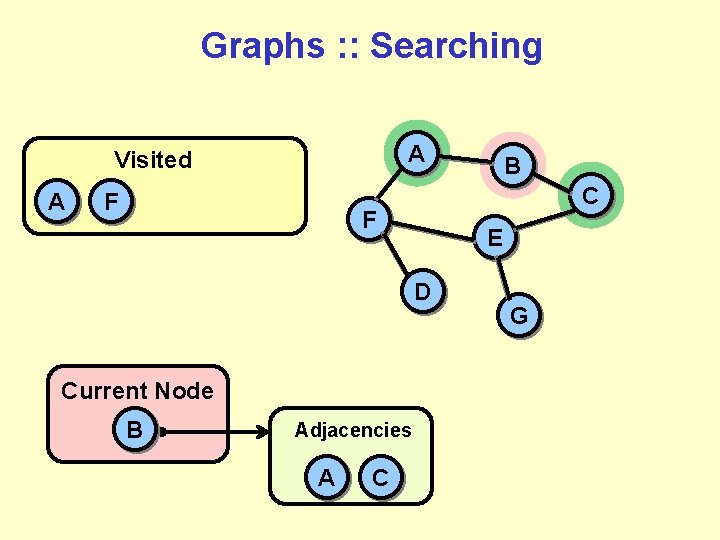
Graphs : : Searching A Visited A F C F E D Current Node B Adjacencies A C B G

Graphs : : Searching A Visited A F C F E D Current Node B Adjacencies A C B G

Graphs : : Searching A Visited A F B C F E D Current Node B B G

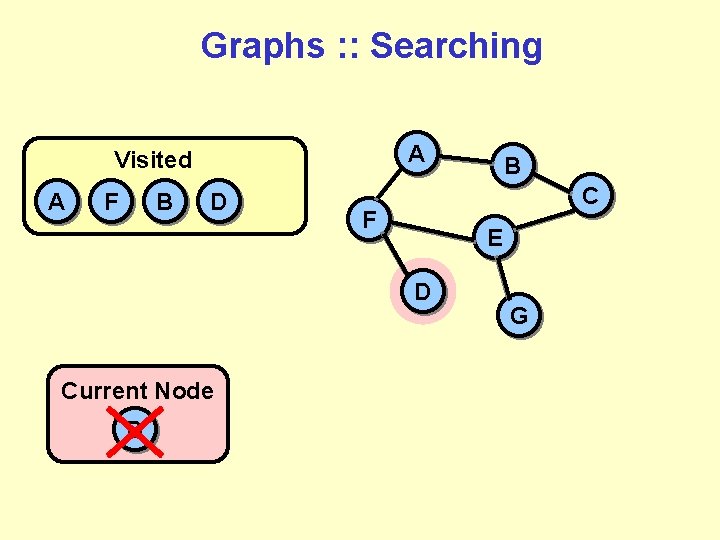
Graphs : : Searching A Visited A F B C F E D Current Node D Adjacencies F B G

Graphs : : Searching A Visited A F B D C F E D Current Node D B G

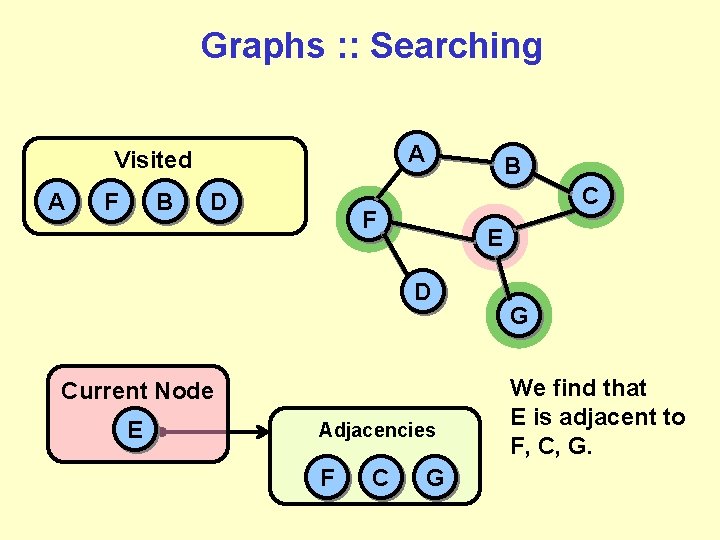
Graphs : : Searching A Visited A F B D B C F E D Current Node E Adjacencies F C G G We find that E is adjacent to F, C, G.

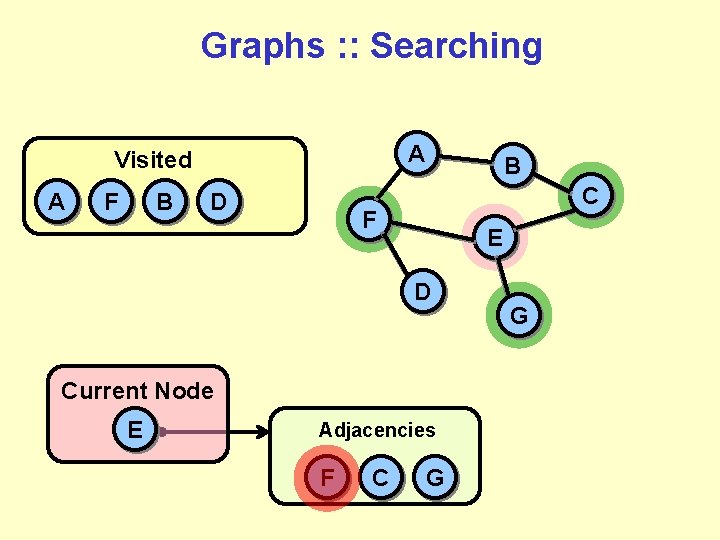
Graphs : : Searching A Visited A F B D B C F E D Current Node E Adjacencies F C G G

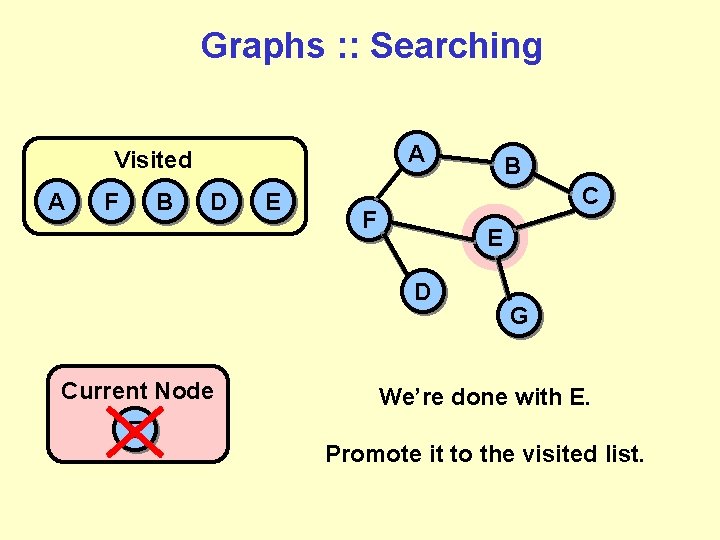
Graphs : : Searching A Visited A F B D E C F E D Current Node E B G We’re done with E. Promote it to the visited list.

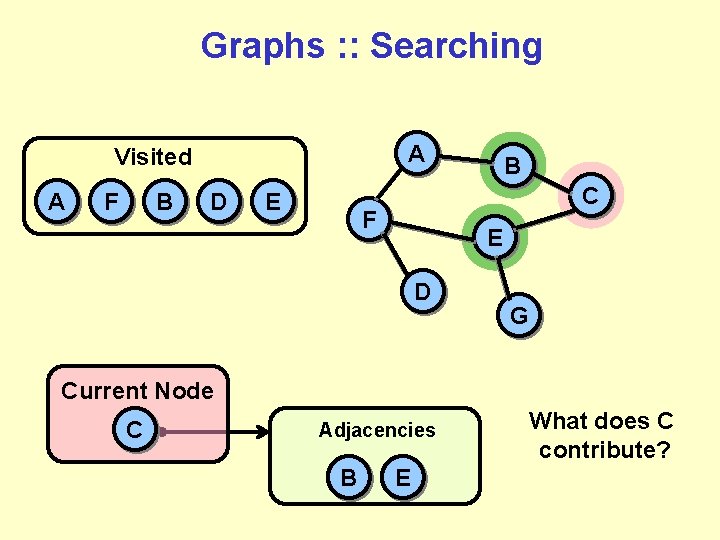
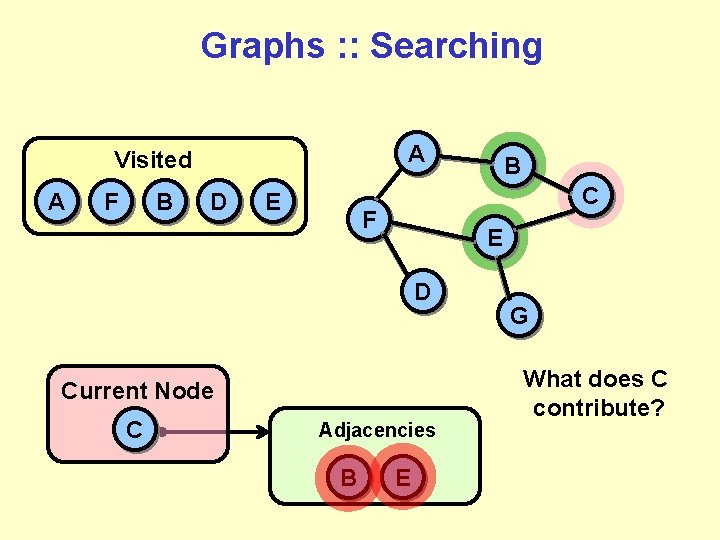
Graphs : : Searching A Visited A F B D E B C F E D G Current Node C Adjacencies B E What does C contribute?

Graphs : : Searching A Visited A F B D E C F E D Current Node C Adjacencies B B E G What does C contribute?

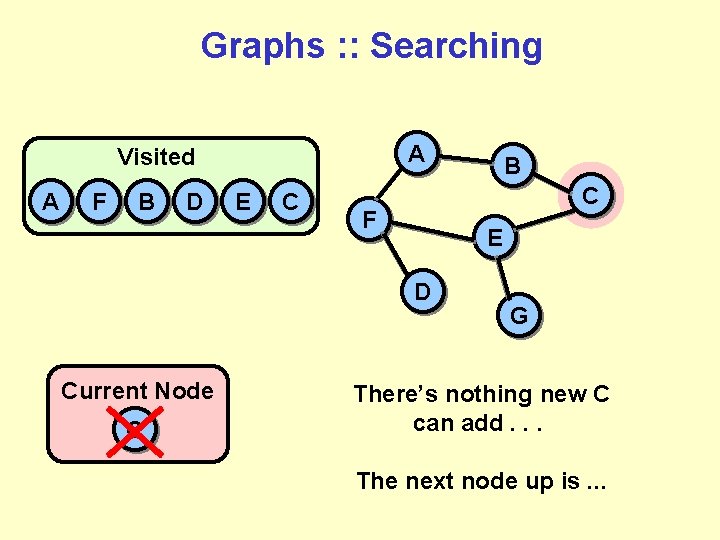
Graphs : : Searching A Visited A F B D E C C F E D Current Node C B G There’s nothing new C can add. . . The next node up is. . .

Graphs : : Searching A Visited A F B D E C C F E D Current Node G G B G G, the goal node. We’re done.

Whew.

public class Node { private String cityname; private Linked. List<Node> gets. To; boolean has. Route(Node to) { if (this. equals(to)) return true; else { for (Node c : this. gets. To) { if (c. has. Route(to)) { return true; } } return false; } } }

public class Node { private String cityname; private Linked. List<Node> gets. To; boolean has. Route(Node to, Linked. List<Node> visited) { if (this. equals(to)) return true; else { for (Node c : this. gets. To) { if (c. has. Route(to)) { return true; } } return false; } } }

public class Node { private String cityname; private Linked. List<Node> gets. To; boolean has. Route(Node to, Linked. List<Node> visited) { if (this. equals(to)) return true; else if (visited. contains(this)) return false; else { for (Node c : this. gets. To) { if (c. has. Route(to)) { return true; } } return false; } } }

public class Node { private String cityname; private Linked. List<Node> gets. To; boolean has. Route(Node to, Linked. List<Node> visited) { if (this. equals(to)) return true; else if (visited. contains(this)) return false; else { visited. add(this); for (Node c : this. gets. To) { if (c. has. Route(to)) { return true; } } return false; } } }

G. has. Route(manc, prov) Manchester Boston Providence Worcester Hartford

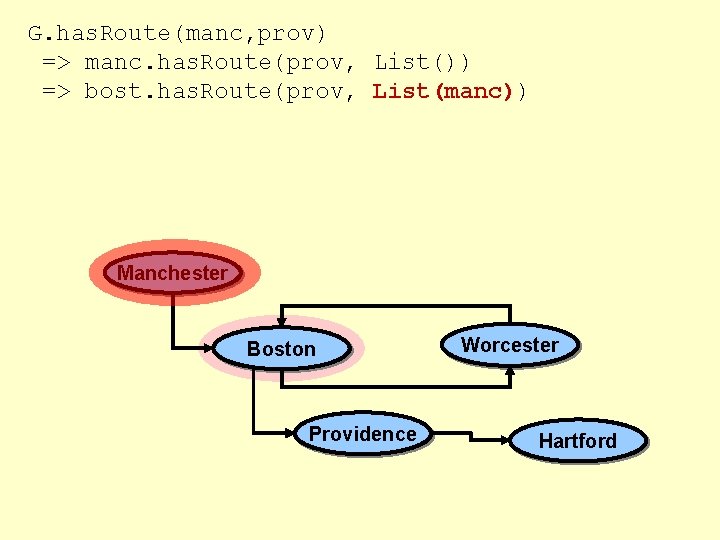
G. has. Route(manc, prov) => manc. has. Route(prov, List()) Manchester Boston Providence Worcester Hartford

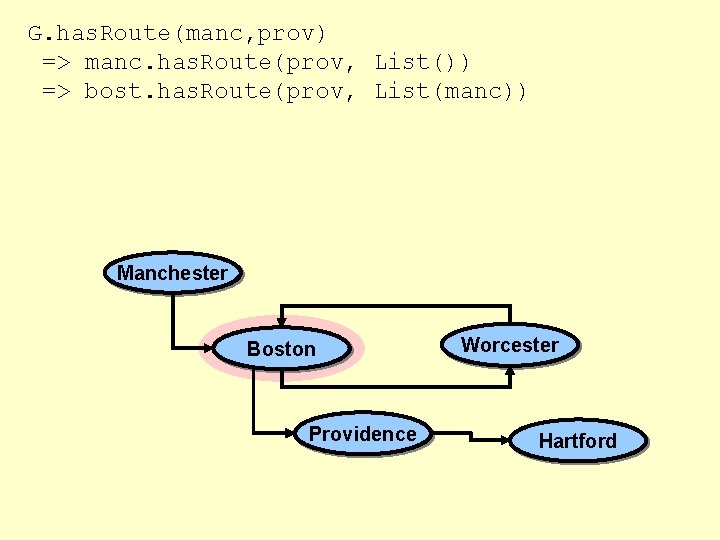
G. has. Route(manc, prov) => manc. has. Route(prov, List()) => bost. has. Route(prov, List(manc)) Manchester Boston Providence Worcester Hartford

G. has. Route(manc, prov) => manc. has. Route(prov, List()) => bost. has. Route(prov, List(manc)) Manchester Boston Providence Worcester Hartford

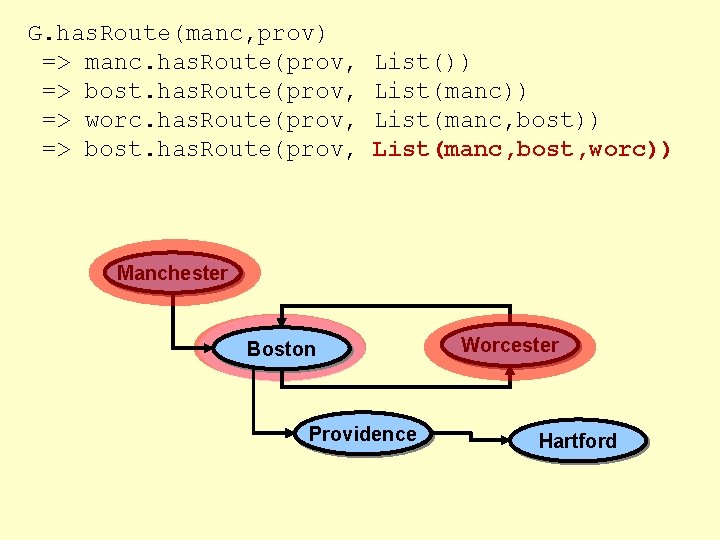
G. has. Route(manc, prov) => manc. has. Route(prov, List()) => bost. has. Route(prov, List(manc)) => worc. has. Route(prov, List(manc, bost)) Manchester Boston Providence Worcester Hartford

G. has. Route(manc, prov) => manc. has. Route(prov, => bost. has. Route(prov, => worc. has. Route(prov, => bost. has. Route(prov, List()) List(manc, bost)) List(manc, bost, worc)) Manchester Boston Providence Worcester Hartford

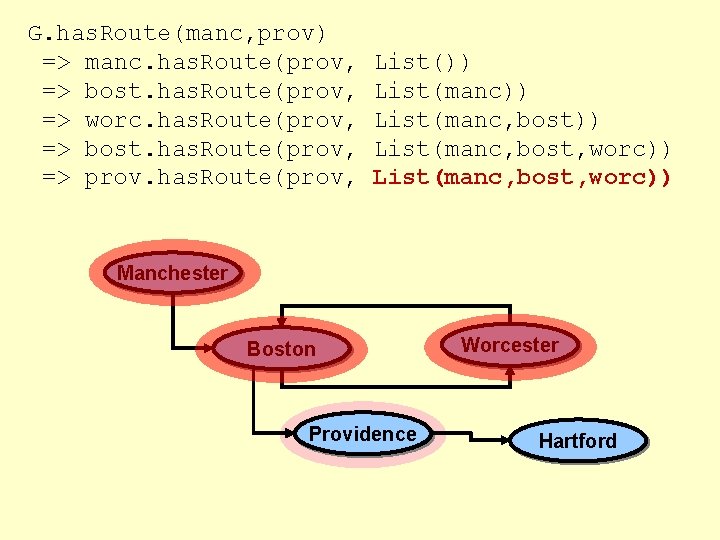
G. has. Route(manc, prov) => manc. has. Route(prov, => bost. has. Route(prov, => worc. has. Route(prov, => bost. has. Route(prov, => prov. has. Route(prov, List()) List(manc, bost)) List(manc, bost, worc)) Manchester Boston Providence Worcester Hartford

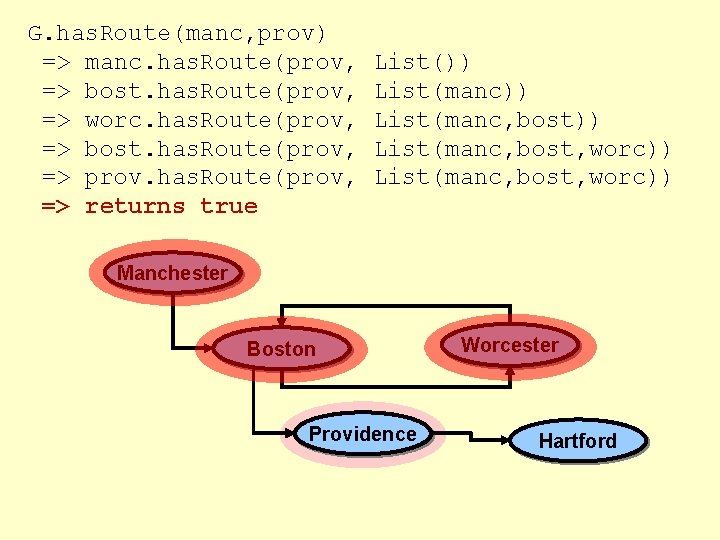
G. has. Route(manc, prov) => manc. has. Route(prov, => bost. has. Route(prov, => worc. has. Route(prov, => bost. has. Route(prov, => prov. has. Route(prov, => returns true List()) List(manc, bost)) List(manc, bost, worc)) Manchester Boston Providence Worcester Hartford

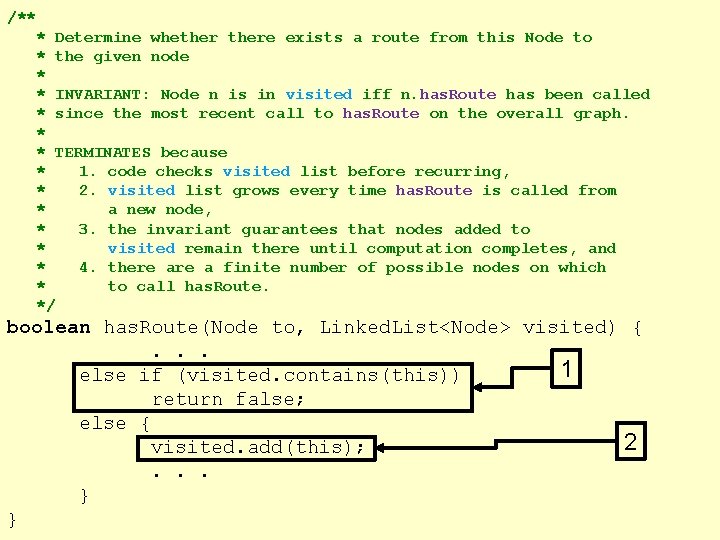
/** * Determine whethere exists a route from this Node to * the given node * * INVARIANT: Node n is in visited iff n. has. Route has been called * since the most recent call to has. Route on the overall graph. * * TERMINATES because * 1. code checks visited list before recurring, * 2. visited list grows every time has. Route is called from * a new node, * 3. the invariant guarantees that nodes added to * visited remain there until computation completes, and * 4. there a finite number of possible nodes on which * to call has. Route. */ boolean has. Route(Node to, Linked. List<Node> visited) {. . . 1 else if (visited. contains(this)) return false; else { 2 visited. add(this); . . . } }

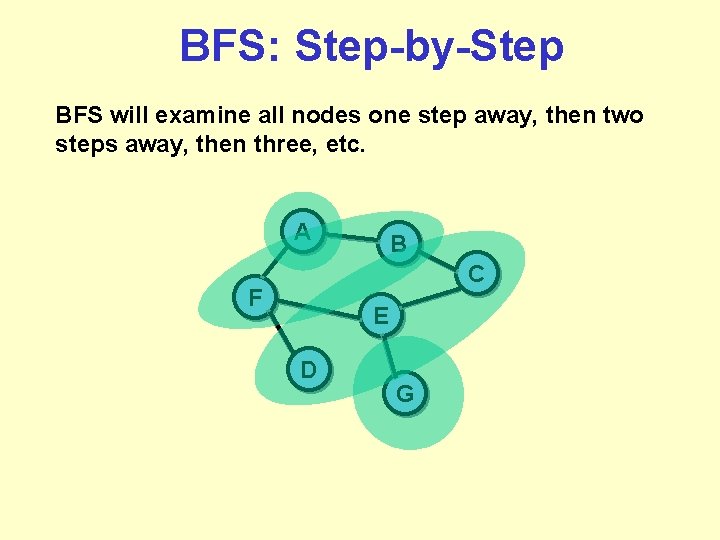
BFS: Step-by-Step BFS will examine all nodes one step away, then two steps away, then three, etc. A B C F E D G

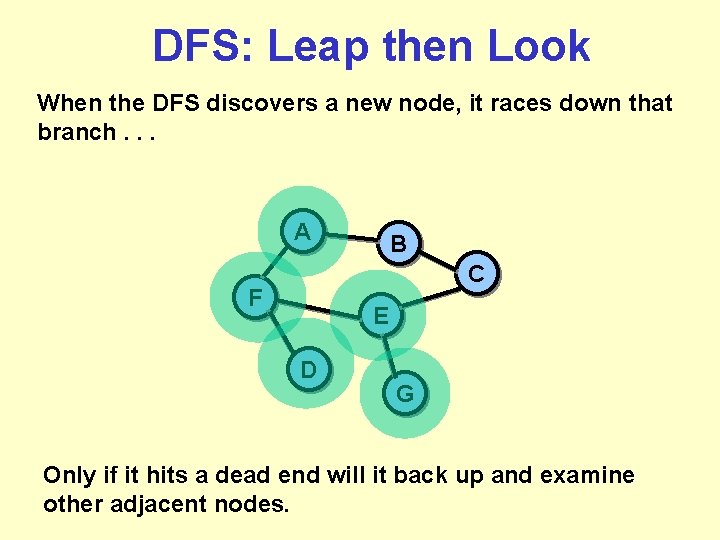
DFS: Leap then Look When the DFS discovers a new node, it races down that branch. . . A B C F E D G Only if it hits a dead end will it back up and examine other adjacent nodes.

Questions?