Algoritmalar DERS 2 Asimptotik Notasyon O ve notasyonlar













































- Slides: 55

Algoritmalar DERS 2 Asimptotik Notasyon • O-, Ω-, ve Θ-notasyonları Yinelemeler • Yerine koyma metodu • Yineleme döngüleri • Özyineleme ağacı • Ana Metot (Master metod) September 12, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson L 2. 1

Asimptotik notasyon O-notasyonu (üst sınırlar): Tüm n ≥ n 0 değerleri için sabitler c > 0, n 0 > 0 ise 0 ≤ f(n) ≤ cg(n) durumunda f(n) = O(g(n)) yazabiliriz. September 12, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson L 2. 2

Asimptotik notasyon O-notasyonu (üst sınırlar): Tüm n ≥ n 0 değerleri için sabitler c > 0, n 0 > 0 ise 0 ≤ f(n) ≤ cg(n) durumunda f(n) = O(g(n)) yazabiliriz. ÖRNEK: 2 n 2 = O(n 3) September 12, 2005 (c = 1, n 0 = 2) Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson L 2. 3

Asimptotik notasyon O-notasyonu (üst sınırlar): Tüm n ≥ n 0 değerleri için sabitler c > 0, n 0 > 0 ise 0 ≤ f(n) ≤ cg(n) durumunda f(n) = O(g(n)) yazabiliriz. ÖRNEK: 2 n 2 = O(n 3) (c = 1, n 0 = 2) fonksiyonlar, değerler değil September 12, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson L 2. 4

Asimptotik notasyon O-notasyonu (üst sınırlar): Tüm n ≥ n 0 değerleri için sabitler c > 0, n 0 > 0 ise 0 ≤ f(n) ≤ cg(n) durumunda f(n) = O(g(n)) yazabiliriz. ÖRNEK: 2 n 2 = O(n 3) fonksiyonlar, değerler değil September 12, 2005 (c = 1, n 0 = 2) komik, “tek yönlü” eşitlik Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson L 2. 5

O-notasyonunun tanımı O(g(n))= { f(n) : tüm n ≥ n 0 değerlerinde c > 0, n 0 > 0 ise ve 0 ≤ f(n) ≤ cg(n) } September 12, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson L 2. 6

O-notasyonunun tanımı O(g(n))= { f(n) : tüm n ≥ n 0 değerlerinde c > 0, n 0 > 0 ise ve 0 ≤ f(n) ≤ cg(n) } ÖRNEK: 2 n 2 ∈ O(n 3) September 12, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson L 2. 7

Ω-notasyonu (alt sınırlar) O-notasyonu bir üst-sınır notasyonudur. f(n) en az O(n 2)'dir demenin bir anlamı yoktur. September 12, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson L 2. 8

Ω-notasyonu (alt sınırlar) O-notasyonu bir üst-sınır notasyonudur. f(n) en az O(n 2)'dir demenin bir anlamı yoktur. Ω(g(n))= { f(n) : tüm n ≥ n 0 değerlerinde c > 0, n 0 > 0 ise ve 0 ≤ cg(n) ≤ f(n) } September 12, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson L 2. 9

Ω-notasyonu (alt sınırlar) O-notasyonu bir üst-sınır notasyonudur. f(n) en az O(n 2)'dir demenin bir anlamı yoktur. Ω(g(n))= { f(n) : tüm n ≥ n 0 değerlerinde c > 0, n 0 > 0 ise ve 0 ≤ cg(n) ≤ f(n) } ÖRNEK: September 12, 2005 n = Ω (lg n) (c = 1, n 0 = 16) Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson L 2. 10

Ω-notasyonu (alt sınırlar)

Θ-notasyonu (sıkı sınırlar) Θ(g(n)) = O(g(n)) ∩ Ω(g(n)) September 12, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson L 2. 12

Θ-notasyonu (sıkı sınırlar) Θ(g(n)) = O(g(n)) ∩ Ω(g(n)) ÖRNEK: September 12, 2005 1 2 n 2 − 2 n = Θ(n 2 ) Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson L 2. 13

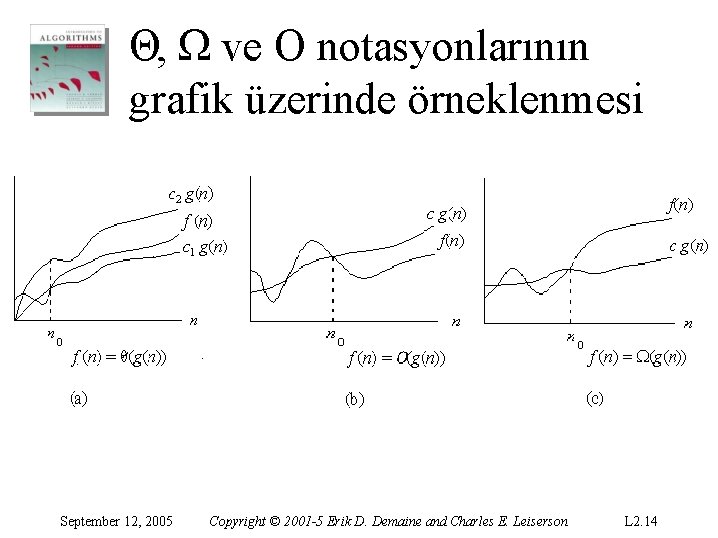
Θ, Ω ve O notasyonlarının grafik üzerinde örneklenmesi September 12, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson L 2. 14

ο ve ω notasyonları O-notasyonu ve Ω-notasyonu ≤ ve ≥ gibidir. o-notasyonu ve ω-notasyonu < ve > gibidir. . o(g(n))= { f(n) : tüm n ≥ n 0 değerlerinde c > 0 sabiti için n 0 sabiti varsa 0 ≤ f(n) ≤ cg(n) } ÖRNEK: September 12, 2005 2 n 2 = o(n 3) (n 0 = 2/c) Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson L 2. 15

ο ve ω notasyonları O-notasyonu ve Ω-notasyonu ≤ ve ≥ gibidir. o-notasyonu ve ω-notasyonu < ve > gibidir. . o(g(n))= { f(n) : tüm n ≥ n 0 değerlerinde c > 0 sabiti için n 0 sabiti varsa 0 ≤ f(n) ≤ cg(n) } ÖRNEK: September 12, 2005 n = ω(lg n) (n 0 = 1+1/c) Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson L 2. 16

ο ve ω notasyonları

Sorular

Yinelemelerin çözümü • Ders 1' deki birleştirme sıralaması analizi bir yinelemeyi çözmemizi gerektirmişti. • Yinelemeler integral, türev, v. s. denklemlerinin çözümlerine benzer. • Yinelemelerin "böl-ve-fethet" algoritmalarına uygulanması. September 12, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson L 2. 19

Özyinelemelerin Çözümü

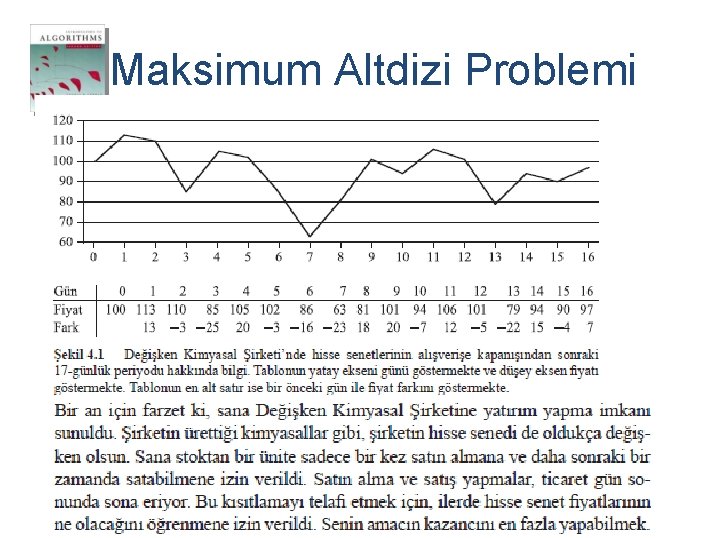
Maksimum Altdizi Problemi

Maksimum Altdizi Problemi

Maksimum Altdizi Problemi

Maksimum Altdizi Problemi

Yerine koyma metodu (yöntemi) En genel yöntem: 1. Çözümün şeklini tahmin edin. 2. Tümevarım ile doğrulayın. 3. Sabitleri çözün. September 12, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson L 2. 25

Yerine koyma metodu (yöntemi) En genel yöntem: 1. Çözümün şeklini tahmin edin. 2. Tümevarım ile doğrulayın. 3. Sabitleri çözün. ÖRNEK: T(n) = 4 T(n/2) + n • T(1) = Θ(1) olduğunu varsayın. • O(n 3)'ü tahmin edin. (O ve Ω ayrı kanıtlayın. ) • k< n için T(k) ≤ ck 3 olduğunu varsayın. • T(n) ≤ cn 3'ü tümevarımla kanıtlayın. September 12, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson L 2. 26

Yerine koyma örneği T (n) = 4 T (n / 2) + n ≤ 4 c(n / 2)3 + n = (c / 2)n 3 + n istenen –kalan = cn 3 − ((c / 2)n 3 − n) istenen ≤ cn 3 (c/2)n 3 – n ≥ 0 olduğu zamanlarda, örneğin, eğer c ≥ 2 ve n ≥ 1 ise. kalan September 12, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson L 2. 27

Örnek (devamı) • Başlangıç koşullarını da ele almalı, yani, tümevarımı taban şıklarına (base cases) dayandırmalıyız. • Taban: T(n) = Θ(1) tüm n < n 0 için, ki n 0 uygun bir sabittir. • 1 ≤ n < n 0 için, elimizde “Θ(1)” ≤ cn 3, olur; yeterince büyük bir c değeri seçersek. September 12, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson L 2. 28

Örnek (devamı) • Başlangıç koşullarını da ele almalı, yani, tümevarımı taban şıklarına (base cases) dayandırmalıyız. • Taban: T(n) = Θ(1) tüm n < n 0 için, ki n 0 uygun bir sabittir. • 1 ≤ n < n 0 için, elimizde “Θ(1)” ≤ cn 3, olur; yeterince büyük bir c değeri seçersek. Bu, sıkı bir sınır değildir ! September 12, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson L 2. 29

Daha sıkı bir üst sınır? T(n) = O(n 2) olup olmadığını kanıtlayacağız. September 12, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson L 2. 30

Daha sıkı bir üst sınır? T(n) = O(n 2) olduğunu kanıtlayacağız. Varsayın ki k < n için T(k) ≤ ck 2 olsun: T (n) = 4 T (n / 2) + n ≤ 4 c(n / 2)2 + n = cn 2 – (– n ) [ istenen –kalan ] ≤ cn 2 September 12, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson L 2. 31

Daha sıkı bir üst sınır? T(n) = O(n 2) olduğunu kanıtlayacağız. Varsayın ki k < n için T(k) ≤ ck 2 olsun: T (n) = 4 T (n / 2) + n ≤ 4 c(n / 2)2 + n = cn 2 – (– n ) ≤ cn 2 Yanlış c > 0 için eşitsizlik doğru değildir. Kaybettik. September 12, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson L 2. 32

Üst Sınır Belirleme

Özyineleme-ağacı metodu • Özyineleme-ağacı, bir algoritmadaki özyineleme uygulamasının maliyetini (zamanı) modeller. • Özyineleme-ağacı metodu, bazen güvenilir olmayabilir. • Öte yandan özyineleme-ağacı metodu "öngörü" olgusunu geliştirir. • Özyineleme-ağacı metodu "yerine koyma metodu" için gerekli tahminlemelerde yararlıdır. September 12, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson L 2. 34

Özyineleme-ağacı metodu

Özyineleme-ağacı metodu

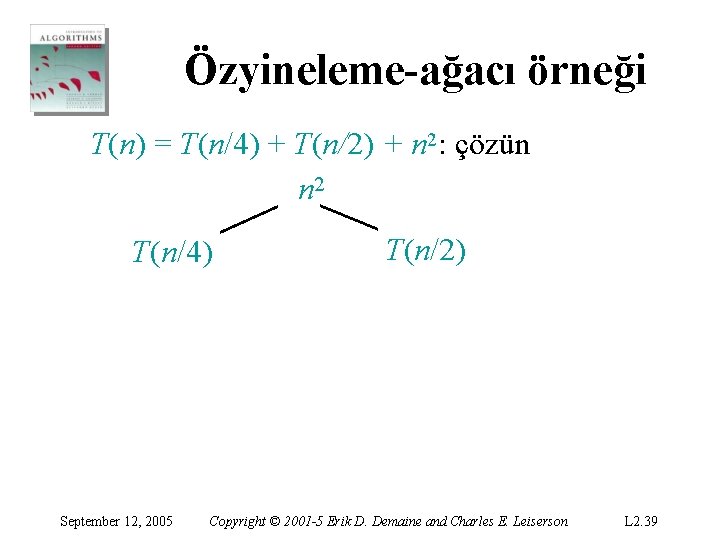
Özyineleme-ağacı örneği T(n) = T(n/4) + T(n/2) + n 2: çözün September 12, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson L 2. 37

Özyineleme-ağacı örneği T(n) = T(n/4) + T(n/2) + n 2: çözün T(n) September 12, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson L 2. 38

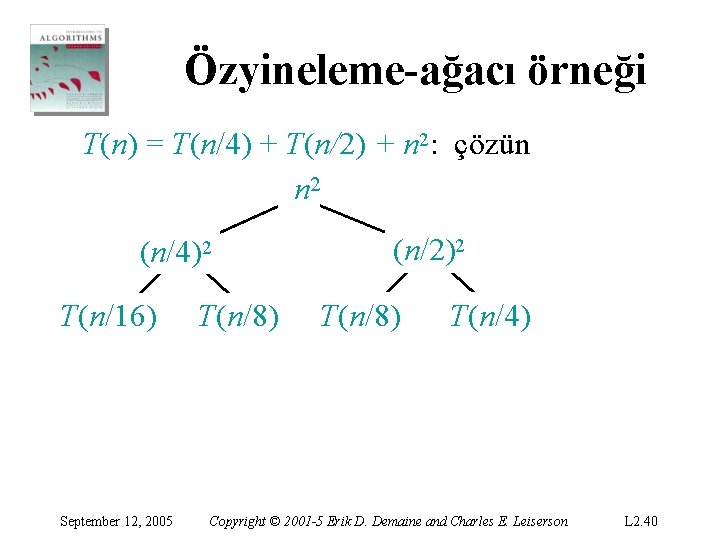
Özyineleme-ağacı örneği T(n) = T(n/4) + T(n/2) + n 2: çözün n 2 T(n/4) September 12, 2005 T(n/2) Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson L 2. 39

Özyineleme-ağacı örneği T(n) = T(n/4) + T(n/2) + n 2: çözün n 2 (n/4)2 T(n/16) September 12, 2005 T(n/8) (n/2)2 T(n/8) T(n/4) Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson L 2. 40

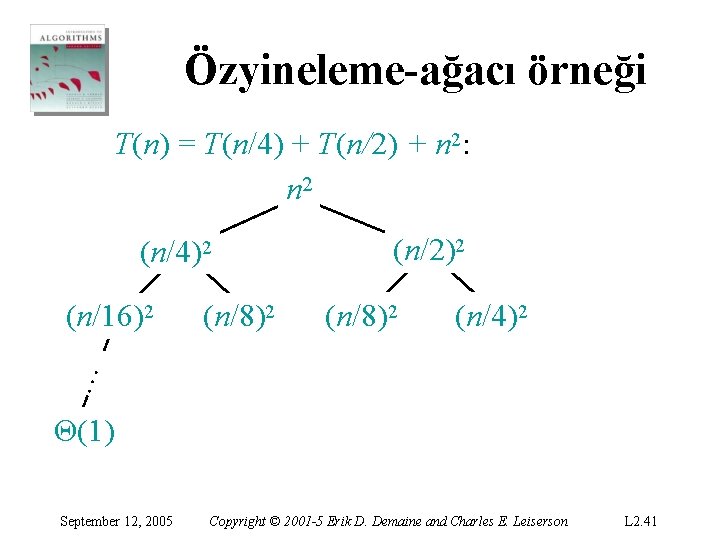
Özyineleme-ağacı örneği T(n) = T(n/4) + T(n/2) + n 2: n 2 (n/4)2 (n/8)2 (n/4)2 … (n/16)2 (n/2)2 Θ(1) September 12, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson L 2. 41

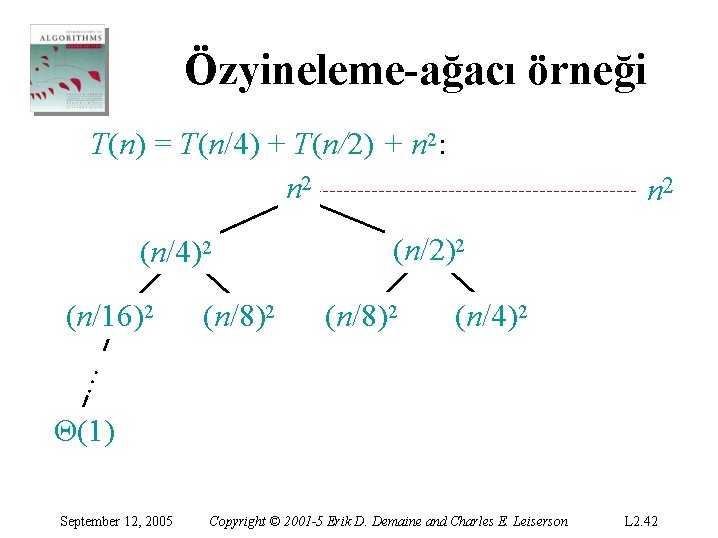
Özyineleme-ağacı örneği T(n) = T(n/4) + T(n/2) + n 2: n 2 (n/4)2 (n/8)2 (n/2)2 (n/8)2 (n/4)2 … (n/16)2 n 2 Θ(1) September 12, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson L 2. 42

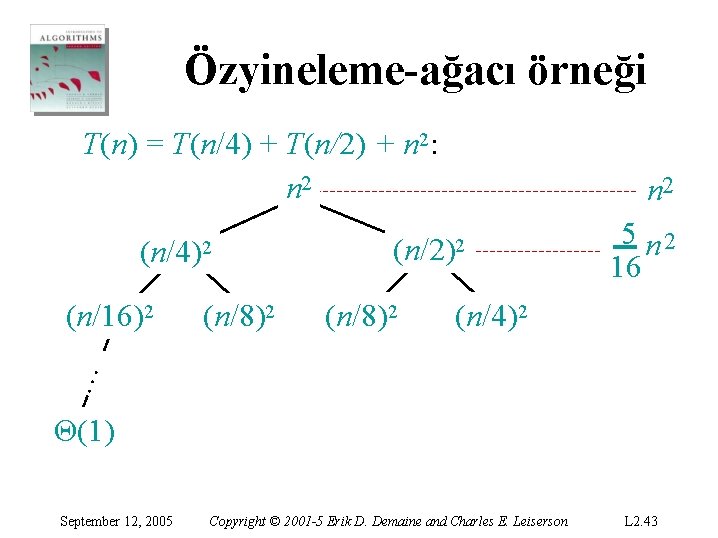
Özyineleme-ağacı örneği T(n) = T(n/4) + T(n/2) + n 2: n 2 (n/4)2 (n/8)2 (n/2)2 (n/8)2 5 n 2 16 (n/4)2 … (n/16)2 n 2 Θ(1) September 12, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson L 2. 43

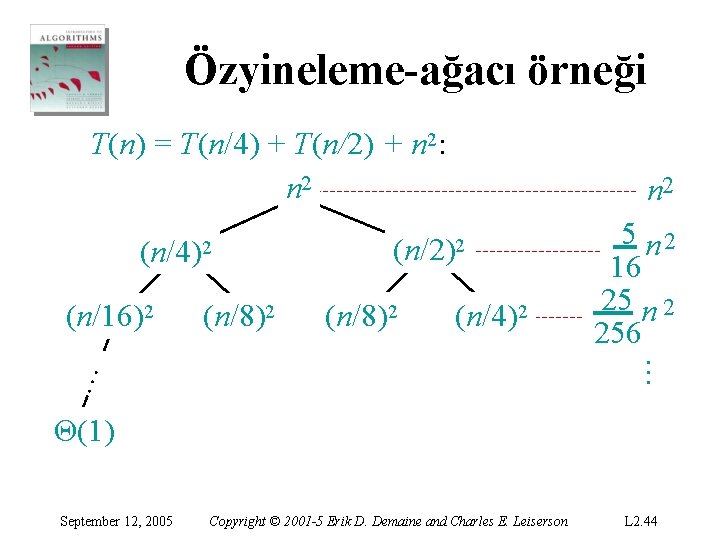
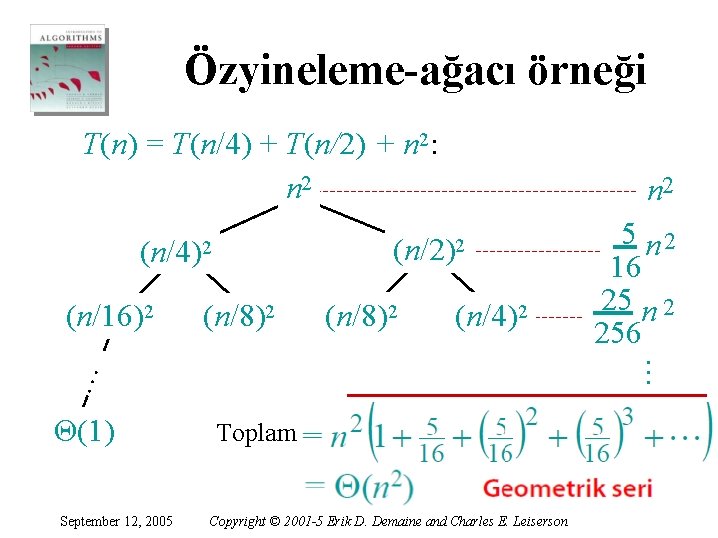
Özyineleme-ağacı örneği T(n) = T(n/4) + T(n/2) + n 2: n 2 (n/4)2 (n/8)2 (n/4)2 5 n 2 16 25 n 2 256 … (n/8)2 (n/2)2 … (n/16)2 n 2 Θ(1) September 12, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson L 2. 44

Özyineleme-ağacı örneği T(n) = T(n/4) + T(n/2) + n 2: n 2 (n/2)2 (n/4)2 (n/8)2 (n/4)2 Θ(1) September 12, 2005 5 n 2 16 25 n 2 256 … (n/8)2 … (n/16)2 n 2 Toplam Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson

Ana Metod (The Master Method) Ana method aşağıda belirtilen yapıdaki yinelemelere uygulanır: T(n) = a T(n/b) + f (n) , burada a ≥ 1, b > 1, ve f asimptotik olarak pozitiftir. September 12, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson L 2. 46

Üç yaygın uygulama f (n)'i nlogba ile karşılaştırın: 1. Daha küçük olma durumu f (n) = O(nlogba – ε) ε > 0 sabiti durumunda • f (n) polinomsal olarak nlogba göre daha yavaş büyür (nε faktörü oranında). ÇÖZÜM: T(n) = Θ(nlogba). September 12, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson L 2. 47

Üç yaygın uygulama f (n)'i nlogba ile karşılaştırın: 1. f (n) = O(nlogba – ε) ε > 0 sabiti durumunda; • f (n) polinomsal olarak nlogba göre daha yavaş büyür(nε faktörü oranında). Çözüm: T(n) = Θ(nlogba). 2. Yaklaşık eşit olma durumu f (n) = Θ(nlogba ) • f (n) ve nlogba benzer oranlarda büyürler. Çözüm: T(n) = Θ(nlogba lgn). September 12, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson L 2. 48

Üç yaygın uygulama f (n)'i nlogba ile karşılaştırın: 3. Daha büyük olma durumu f (n) = Ω(nlogba + ε) ε > 0 sabiti durumunda; • f (n) polinomsal olarak nlogba 'ye göre daha hızlı büyür ( nε faktörü oranında), ve f (n), düzenlilik koşulunu af (n/b) ≤ cf (n) durumunda, c < 1 olmak kaydıyla karşılar. Çözüm: T(n) = Θ(f (n)). September 12, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson L 2. 49

Örnekler Örnek. T(n) = 4 T(n/2) + n a = 4, b = 2 ⇒ nlogba = n 2; f (n) = n. Durum 1: f (n) = O(n 2 – ε) ε = 1 için. ∴ T(n) = Θ(n 2). September 12, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson L 2. 50

Örnekler Ör. T(n) = 4 T(n/2) + n a = 4, b = 2 ⇒ nlogba = n 2; f (n) = n. Durum 1: f (n) = O(n 2 – ε) ε = 1 için. ∴ T(n) = Θ(n 2). Ör. T(n) = 4 T(n/2) + n 2 a = 4, b = 2 ⇒ nlogba = n 2; f (n) = n 2. Durum 2: f (n) = Θ(n 2) olduğu için ∴ T(n) = Θ(n 2 lg n). September 12, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson L 2. 51

Örnekler Ör. T(n) = 4 T(n/2) + n 3 a = 4, b = 2 ⇒ nlogba = n 2; f (n) = n 3. DURUM 3: f (n) = Ω(n 2 + ε) ε = 1 için ve 4(n/2)3 ≤ cn 3 (düz. koş. ) c = 1/2 için. ∴ T(n) = Θ(n 3). September 12, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson L 2. 52

Örnekler Ör. T(n) = 4 T(n/2) + n 3 a = 4, b = 2 ⇒ nlogba = n 2; f (n) = n 3. DURUM 3: f (n) = Ω(n 2 + ε) ε = 1 için ve 4(n/2)3 ≤ cn 3 (düz. koş. ) c = 1/2 için. ∴ T(n) = Θ(n 3). Ör. T(n) = 4 T(n/2) + n 2/lg n a = 4, b = 2 ⇒ nlogba = n 2; f (n) = n 2/lg n. Ana metod geçerli değil. Özellikle, ε > 0 olan sabitler için nε = ω(lg n) elde edilir. September 12, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson L 2. 53

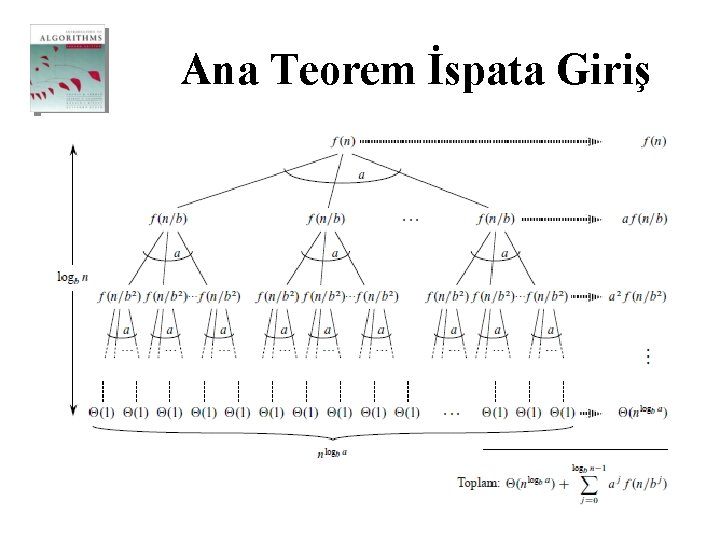
Ana Teorem İspata Giriş

Appendix/EK: Geometrik seriler 2 1 + x +. . . + x 2 1 + x +. . . = September 12, 2005 n n+1 1− x ; x ≠ 1 için = 1− x 1 ; |x| < 1 için 1− x Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson L 2. 55
 Yerine koyma metodu algoritma analizi
Yerine koyma metodu algoritma analizi Asimptotik notasyonlar örnekleri
Asimptotik notasyonlar örnekleri Graflar ve algoritmalar
Graflar ve algoritmalar Notasyon kağıdı
Notasyon kağıdı Keadaan dari kompleksitas waktu
Keadaan dari kompleksitas waktu Asimptotik sapmasızlık nedir
Asimptotik sapmasızlık nedir Asimptotik sapmasızlık nedir
Asimptotik sapmasızlık nedir Notasi asimtotik adalah
Notasi asimtotik adalah Kurum yönetimi ders notları
Kurum yönetimi ders notları Limnoloji ders notları
Limnoloji ders notları Dou ders
Dou ders Tarımsal pazarlama ders notları
Tarımsal pazarlama ders notları Ilkokuma yazma ders planı örneği
Ilkokuma yazma ders planı örneği Xivders
Xivders Hacettepe ders seçim
Hacettepe ders seçim Yyb dersi
Yyb dersi üst yazı örneği
üst yazı örneği Ders planı hazırlama aşamaları
Ders planı hazırlama aşamaları Medya ekonomisi ders notları
Medya ekonomisi ders notları Ekonoms
Ekonoms Hayvancılık ekonomisi ders notları
Hayvancılık ekonomisi ders notları Benzetim ders notları
Benzetim ders notları Sosyal güvenlik teorisi ders notları
Sosyal güvenlik teorisi ders notları Dtcf açık ders
Dtcf açık ders Derin olan kuyu değil kısa olan iptir karikatür
Derin olan kuyu değil kısa olan iptir karikatür Hayat bilgisi nedir
Hayat bilgisi nedir Tarımsal yapılar ve sulama ders notları
Tarımsal yapılar ve sulama ders notları Pozitivizm nedir
Pozitivizm nedir Ntp dersi
Ntp dersi Ttas hangi ders
Ttas hangi ders Deuzem
Deuzem Sensörler ve transdüserler ders notları pdf
Sensörler ve transdüserler ders notları pdf Klorpentan
Klorpentan Eğitim ekonomisi ders notları
Eğitim ekonomisi ders notları Html ders notları
Html ders notları Douonlinesinav
Douonlinesinav Excel ders notları
Excel ders notları Gymnospermae ders notları
Gymnospermae ders notları Ayetel kürsi anlamı 8.sınıf ders kitabı
Ayetel kürsi anlamı 8.sınıf ders kitabı Nmerk
Nmerk Kapilarite nedir
Kapilarite nedir Kurum yönetimi ders notları
Kurum yönetimi ders notları Prof. dr. sultan öztürk
Prof. dr. sultan öztürk Ders çalışmaya nereden başlayacağımı bilmiyorum
Ders çalışmaya nereden başlayacağımı bilmiyorum Neden ders çalışıyoruz
Neden ders çalışıyoruz Allosterik enzimler
Allosterik enzimler Verimli ders çalışma veli sunumu
Verimli ders çalışma veli sunumu Dağıtık sistemler örnek
Dağıtık sistemler örnek Recep tayyip erdoğan üniversitesi formasyon
Recep tayyip erdoğan üniversitesi formasyon Işitsel zeka nasıl ders çalışmalı
Işitsel zeka nasıl ders çalışmalı Matlab ders notları
Matlab ders notları Muamelat güdüsü nedir
Muamelat güdüsü nedir Etkili ders anlatma teknikleri
Etkili ders anlatma teknikleri Kaynakçada kitap nasıl yazılır
Kaynakçada kitap nasıl yazılır Autocad ders notları
Autocad ders notları Sorgunmehmetakifersoyoo
Sorgunmehmetakifersoyoo













































































