Algoritmalar Ders En II 15 Kk rten Aalar

Algoritmalar Ders En II 15 Küçük Örten Ağaçlar 1

ÖN KÜÇÜK ÖRTEN AĞAÇLAR

ÖRTEN AĞAÇ G=(V, E) bağlantılı çizgesinin örten ağacı Bir ağaçtır V kümesinin tüm elemanları bu ağacın düğümleridir G örten ağaç B A A C E D F B Örten ağaçta |V| - 1 kiriş olur. C D E F

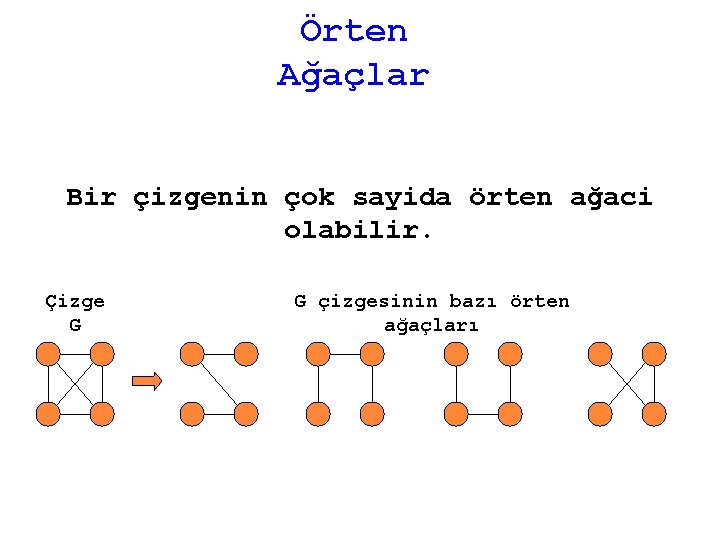
Örten Ağaçlar Bir çizgenin çok sayida örten ağaci olabilir. Çizge G G çizgesinin bazı örten ağaçları

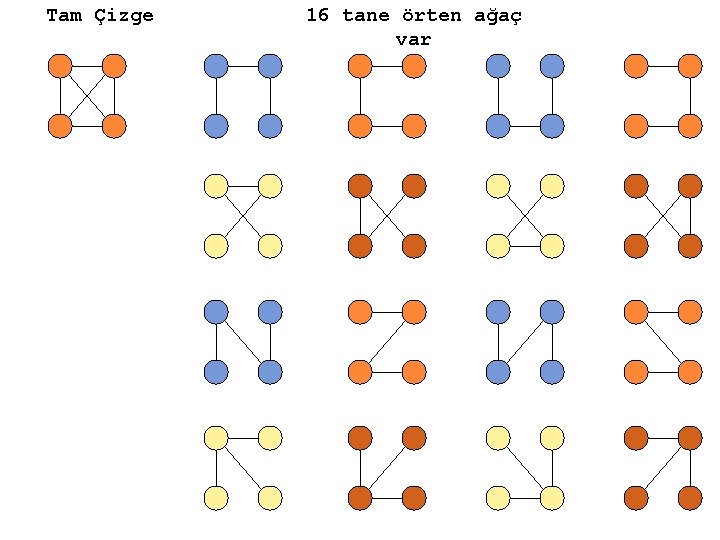
Tam Çizge 16 tane örten ağaç var

ÖRTEN AĞAÇLARİN TOPLAM SAYİSİ n köşeli bir tam çizgenin n (n-2) formülü) 10098 = 10196 sayıda örten ağaçı var (Cayley Bir yılda 315576*106 saniye var. Bir nanosaniye =(10 -9) saniye. Bir yılda 315576*1015 < 1021 nanosaniye var. 100 köşeli çizgenin tüm örten ağaçlarını 10175 yıldan daha uzun sürede bulabiliriz. (Bir işlemi bir nanosaniyede yapabilirsek)

EN KÜÇÜK ÖRTEN AĞAÇ Giriş: Yönsüz bağlantılı çizge G = (V, E) and ağırlık fonksiyonu w : E→R, Çıkış: En küçük örten ağaç T : tüm köşeleri birleştiren ve değeri en küçük olan ağaç Açgözlü algoritmalar Genel en küçük ağaç algoritması Kruskal algoritması Prim algoritması

AÇGÖZLÜ YAKLAŞİM İÇİN TEMEL Aşağıdaki teorem doğrudur: Teorem. T ağacı G = (V, E) çizgesinin en küçük örten ağacı, S V olsun ve (u, v) ∈ E kirişi S kümesindeki köşeleri S – V kümesindeki köşelere birleştiren en küçük ağırlıklı kiriş olsun. Bu durumda (u, v) ∈ T. 8

BÜYÜYEN EN KÜÇÜK ÖRTEN AĞAÇ Genel algoritma Her adımda en küçük ağaç bir kiriş büyüyerek oluşturulur A kümesi kirişler kümesi olsun ve bu küme bir en küçük örten ağacın kirişlerinin altkümesi olsun Her adımda A kümesinin yukarıdaki özelliğini bozmayacak bir (u, v) kirişi buluyoruz ve A kümesine ekliyoruz: A {(u, v)} kümesi de bir en küçük örten ağacın kirişler kümesinin altkümesidir (u, v) kirişine güvenli kiriş denir. 9

GENERIC-MST 10

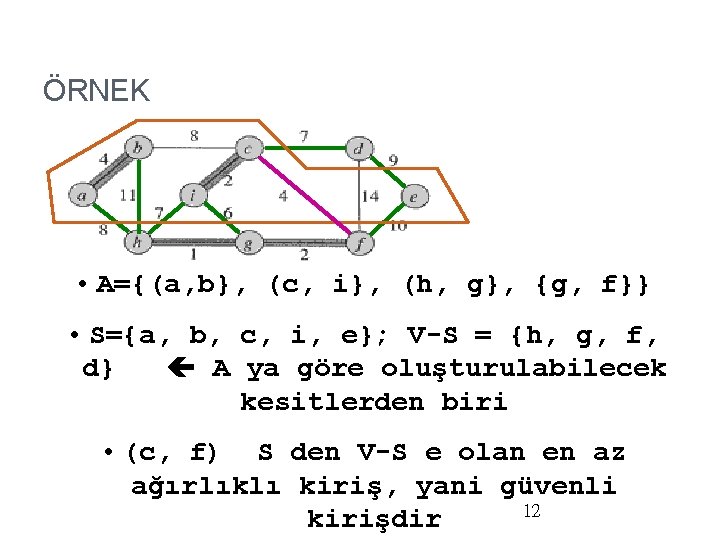
GÜVENLİ KİRİŞ NASİL BULUNUR? A kümesi bir en küçük örten ağacın kirişler kümesi olan E nin altkümesi, (S, V-S) ise G nin A ya göre bir kesiti olsun. (Yani A daki kirişlerin her iki ucu ya S kümesindedir, ya da V-S kümesindedir. ) (u, v) kirişi G nin S kümesindeki köşeleri V-S kümesindeki köşelere birleştiren en küçük ağırlıklı kirişi olsun. Bu durumda (u, v) kirişi A için güvenli kiriş olur.

ÖRNEK • A={(a, b}, (c, i}, (h, g}, {g, f}} • S={a, b, c, i, e}; V-S = {h, g, f, d} A ya göre oluşturulabilecek kesitlerden biri • (c, f) S den V-S e olan en az ağırlıklı kiriş, yani güvenli 12 kirişdir

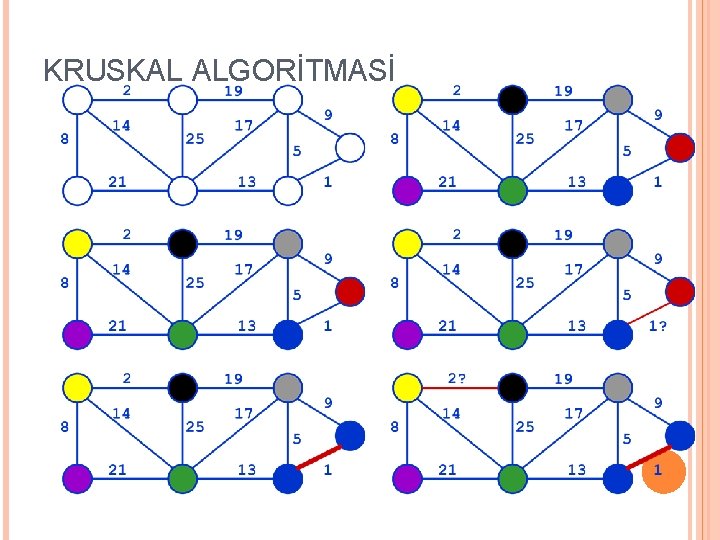
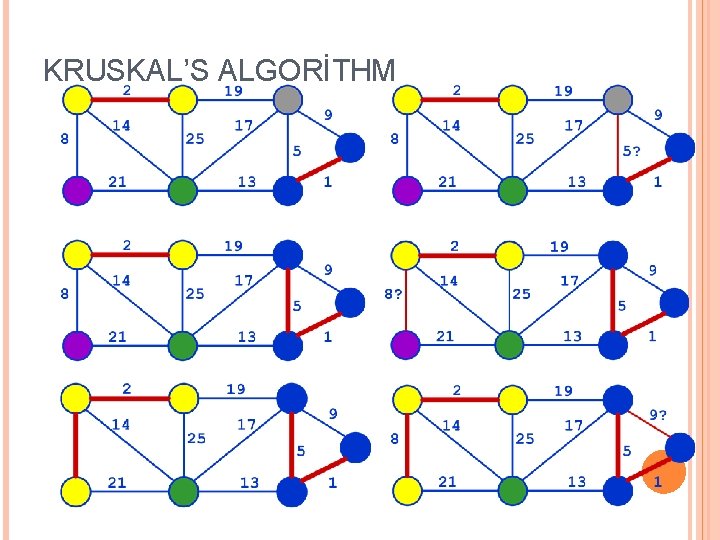
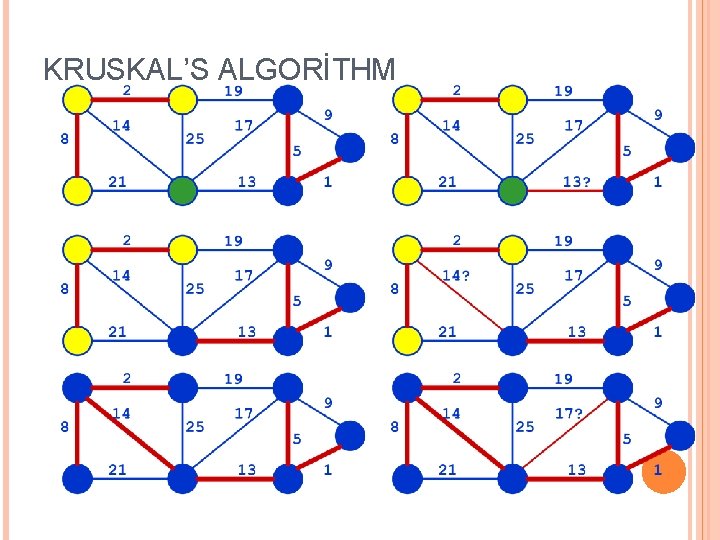
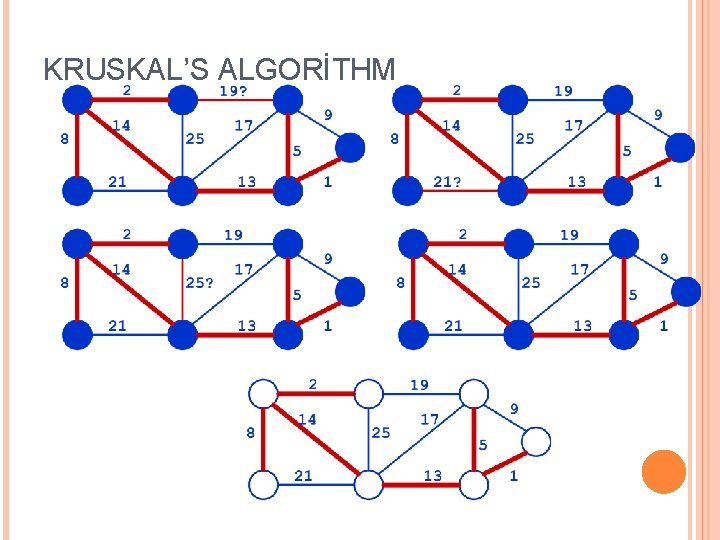
KRUSKAL ALGORİTMASİ Kiriş tabanlı algoritmadır Açgözlü strateji: Kalan kirişler arasında ağırlığı en az olan ve artık seçilmiş kirişlerle döngü oluşturmayacak kirişi seç |V|-1 defa tekrar et

KRUSKAL ALGORİTMASİ Giriş: Ağırlıklı G = (V, E) çizgesi, |V| = n ÇIKIŞ: G nin örten ağacı T Tüm köşeleri içerir, n-1 kirişi var Kirişlerinin toplam ağırlığı en azdır Algoritma: Boş T kümesinden başla, Her adımda kirişleri artan ağırlık sırasıyla ekle Yeni kirişi kabul edilme şartı: eklenen kiriş bir ağaç kirişi olmalıdır (yani bu kiriş T de döngü oluşturmamalıldır) Bu işleme T de n-1 kiriş olana kadar devam edilir

KRUSKAL ALGORİTMASİ MST-Kruskal(G, w) 1 A ¬ Æ 2 for each vertex v Î V[G] do 3 Make-Set(v) //creates set containing v (for initialization) 4 sort the edges of E 5 for each (u, v)ÎE do 6 if Find-Set(u) ¹ Find-Set(v) then // different component 7 A ¬ A {(u, v)} 8 Union(Set(u), Set(v)) // merge 9 return A

KRUSKAL ALGORİTMASİ

KRUSKAL’S ALGORİTHM

KRUSKAL’S ALGORİTHM

KRUSKAL’S ALGORİTHM

KRUSKAL'S ALGORİTHM MST-Kruskal(G, w) 1 A ¬ Æ 2 for each vertex v Î V[G] do // 3 Make-Set(v) 4 sort the edges of E // takes O(V) O(E lg E) // takes O(E) 5 for each (u, v)ÎE, in nondecreasing of weight do 6 if Find-Set(u) ¹ Find-Set(v) then 7 A ¬ A {(u, v)} 8 Union(Set(u), Set(v)) 9 return A