MIT 503 Veri Yaplar ve algoritmalar Sralama algoritmalar









![Kabarcık sıralama başlangıç Kabarcık sıralama p: =giriş_dizi döngü i: =0 p[i]<p[i+1] iken i=i+1; döngü Kabarcık sıralama başlangıç Kabarcık sıralama p: =giriş_dizi döngü i: =0 p[i]<p[i+1] iken i=i+1; döngü](https://slidetodoc.com/presentation_image_h/acc04bc2c2b88712526408ec856a9da4/image-16.jpg)







![quicksort başlangıç quicksort p: =giriş dizi A: =p[orta] sol_dizi=boş dizi sağ_dizi=boş dizi döngü i=0’dan quicksort başlangıç quicksort p: =giriş dizi A: =p[orta] sol_dizi=boş dizi sağ_dizi=boş dizi döngü i=0’dan](https://slidetodoc.com/presentation_image_h/acc04bc2c2b88712526408ec856a9da4/image-25.jpg)






























- Slides: 63

MIT 503 Veri Yapıları ve algoritmalar Sıralama algoritmaları Y. Doç. Dr. Yuriy Mishchenko

Algoritma geliştirme Ders planı – Sıralama algoritmaları ve böl-ve-fethet yöntemi – Naif sıralama – seçme sıralama, ekleme sıralama, kabarcık sıralama – Hızlı sıralama (quicksort), birleşme sıralama (mergesort), hipsort (heapsort) – Özel tamsayı sıralama – sayım sıralama, kova sıralama, radix sıralama

Sıralama sorunu • Sıralama sorunu hatırlatma – Bir sayısal dizi var, N uzunluğunda 15 2 13 11 7 5 2 6 9 – O dizideki sayıların sıralanmış olmasını istiyoruz 2 2 5 6 7 9 11 13 15

Naif sıralama • Naif sıralama algoritmaları – Seçme sıralama – Ekleme sıralama – Kabarcık sıralama

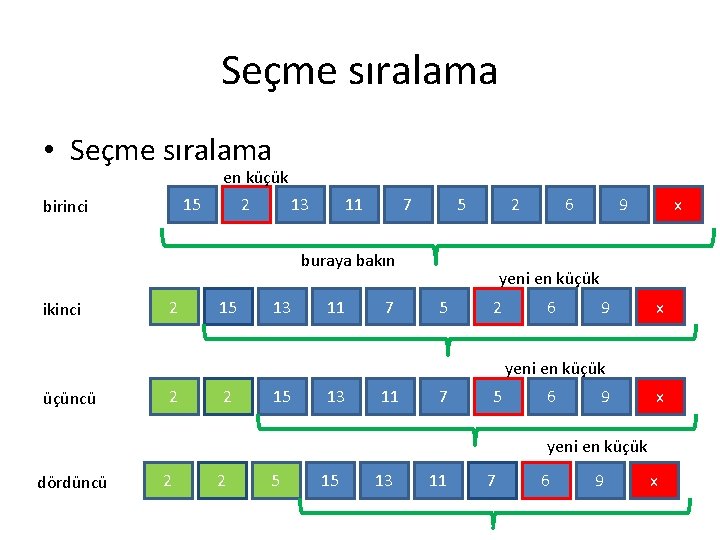
Seçme sıralama • Ana fikri – Çıktı dizisinin birinci pozisyonu için verilen dizideki en küçük sayıyı bulup çıktının 1. pozısyonuna koyuyoruz – Çıktı dizisinin ikinci pozisyonu için verilen dizideki en küçük kalan sayıyı bulup çıktının 2. pozısyonuna koyuyoruz – Üçüncü pozısyon için, verilen dizideki en küçük kalan sayısını bulup tekrar çıktının 3. pozısyonuna koyuyoruz – v. b.

Seçme sıralama • Seçme sıralama 15 birinci en küçük 2 13 11 7 5 2 buraya bakın ikinci 2 15 13 11 7 6 9 x yeni en küçük 5 2 6 9 x yeni en küçük üçüncü 2 2 15 13 11 7 5 6 9 x yeni en küçük dördüncü 2 2 5 15 13 11 7 6 9 x

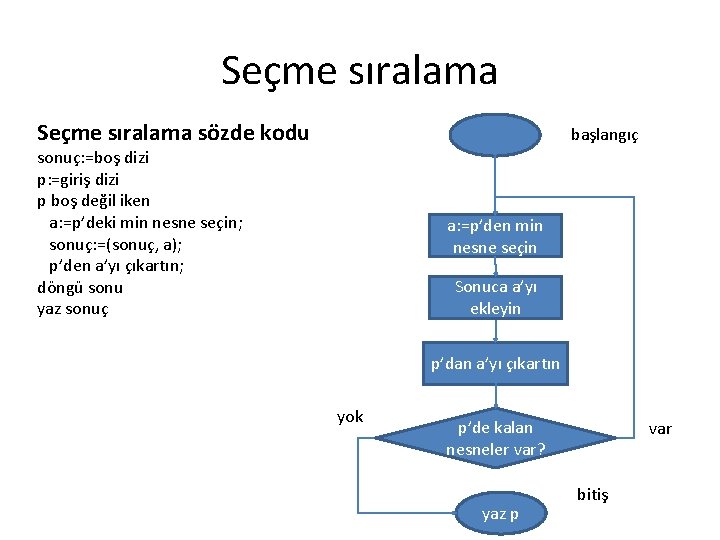
Seçme sıralama sözde kodu başlangıç sonuç: =boş dizi p: =giriş dizi p boş değil iken a: =p’deki min nesne seçin; sonuç: =(sonuç, a); p’den a’yı çıkartın; döngü sonu yaz sonuç a: =p’den min nesne seçin Sonuca a’yı ekleyin p’dan a’yı çıkartın yok p’de kalan nesneler var? yaz p var bitiş

Seçme sıralama • Seçme sıralamada, bütün kalan diziyi tekrar incelememiz lazım • İlk pozısyon için, N sayı incelememiz lazim • İkinci pozısyon için, N-1 sayı incelememiz lazim • Üçüncü pozısyon için, N-2 sayı incelememiz lazim • vb • Toplam, N(N-1)/2=O(N 2) operasyon yapıyoruz

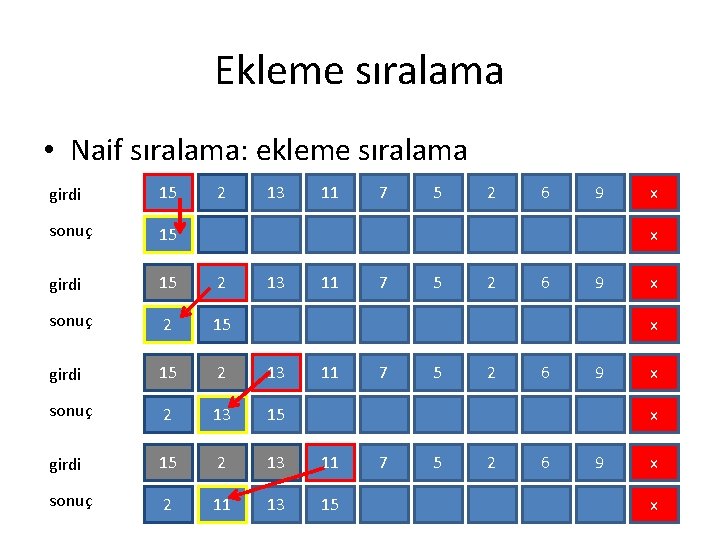
Ekleme sıralama • Ana fikri – Sonucu sıralanmış şekilde baştan oluşturuyoruz – Bunun için, verilen diziden bir sayı alırken o sayıyı her zaman sonuca doğru bir pozisyona ekliyoruz (ama bunun için ikiye bölme kullanmıyoruz) – Doğru pozisyonu bulmak için bütün var olan çıktı dizisini tekrar incelememiz lazım

Ekleme sıralama • Naif sıralama: ekleme sıralama girdi 15 2 13 11 sonuç 15 girdi 15 2 sonuç 2 15 girdi 15 2 13 sonuç 2 13 15 girdi 15 2 13 11 sonuç 2 11 13 15 7 5 2 6 9 x x 13 11 7 5 2 6 9 x x

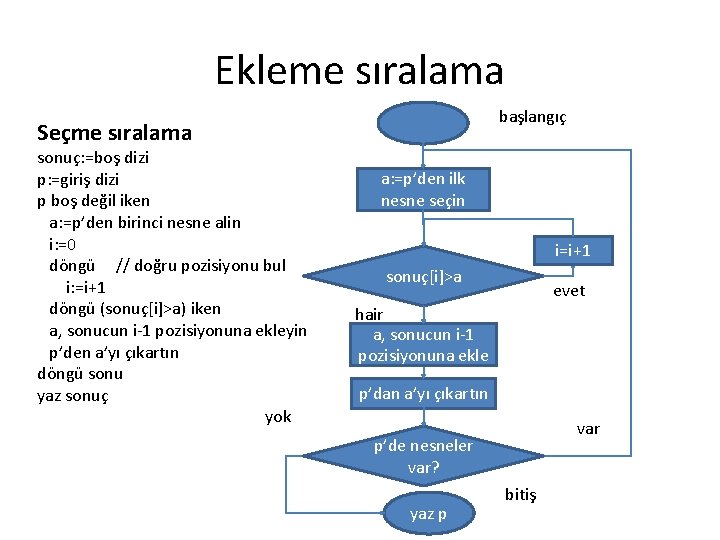
Ekleme sıralama başlangıç Seçme sıralama sonuç: =boş dizi p: =giriş dizi p boş değil iken a: =p’den birinci nesne alin i: =0 döngü // doğru pozisiyonu bul i: =i+1 döngü (sonuç[i]>a) iken a, sonucun i-1 pozisiyonuna ekleyin p’den a’yı çıkartın döngü sonu yaz sonuç yok a: =p’den ilk nesne seçin i=i+1 sonuç[i]>a evet hair a, sonucun i-1 pozisiyonuna ekle p’dan a’yı çıkartın var p’de nesneler var? yaz p bitiş

Ekleme sıralama • Ekleme sıralamada, doğru pozisyonu bulmak için bütün çıktı dızısını incelememiz gerekiyor • Bu nedenle, bu algoritma için ortalama N(N-1)/2=O(N 2) operasyon gerekiyor • Girdi olarak neredeyse sıralanmış dizi varsa, çok hızlı algoritma olabilir (bu durumda daha avantajlı algoritmadır)

Kabarcık sıralama • Kabarcık sıralama, çok popüler algoritmadır ve her zaman “algoritmalar” derslerinde verilir • Ana fikri – Diziyi inceliyoruz – Bir yanlış sırada çift varsa, yani soldaki sayı sağdaki sayı’dan daha büyükse, çiftteki sayıların pozısyonlarını değiştiriyoruz – Sonra var olan diziyi tekrar inceliyoruz, bu şekilde devam ediyoruz

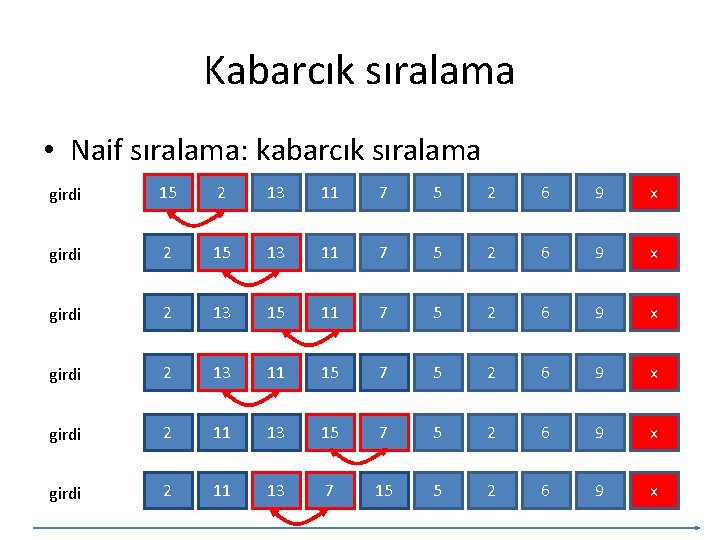
Kabarcık sıralama • Naif sıralama: kabarcık sıralama girdi 15 2 13 11 7 5 2 6 9 x girdi 2 15 13 11 7 5 2 6 9 x girdi 2 13 15 11 7 5 2 6 9 x girdi 2 13 11 15 7 5 2 6 9 x girdi 2 11 13 7 15 5 2 6 9 x

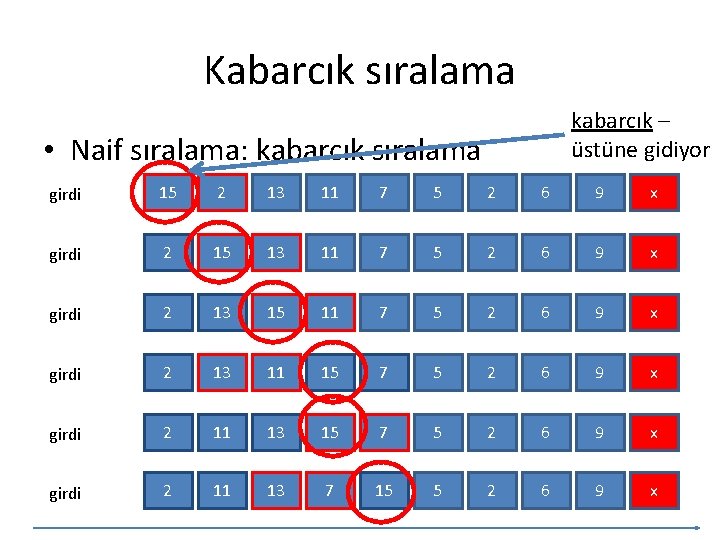
Kabarcık sıralama kabarcık – üstüne gidiyor • Naif sıralama: kabarcık sıralama girdi 15 2 13 11 7 5 2 6 9 x girdi 2 15 13 11 7 5 2 6 9 x girdi 2 13 15 11 7 5 2 6 9 x girdi 2 13 11 15 7 5 2 6 9 x girdi 2 11 13 7 15 5 2 6 9 x
![Kabarcık sıralama başlangıç Kabarcık sıralama p girişdizi döngü i 0 pipi1 iken ii1 döngü Kabarcık sıralama başlangıç Kabarcık sıralama p: =giriş_dizi döngü i: =0 p[i]<p[i+1] iken i=i+1; döngü](https://slidetodoc.com/presentation_image_h/acc04bc2c2b88712526408ec856a9da4/image-16.jpg)
Kabarcık sıralama başlangıç Kabarcık sıralama p: =giriş_dizi döngü i: =0 p[i]<p[i+1] iken i=i+1; döngü eğer p[i], p’nin sonunda ise evet döngüden çıkın; // hiç yanlış sırada // çift bulunmadı p[i] ve p[i+1] değiştirin döngü sonu yaz p i=0 i=i+1 p[i]<p[i+1] evet hair p’nin sonunda? hair p[i] ve p[i+1] değiştirin yaz p bitiş

Kabarcık sıralama • Kabarcık sıralama, ortalama tekrar O(N 2) operasyon gerekiyor • Girdi olarak neredeyse sıralanmış dizi varsa, tekrar onu hızlı sıralayabilir ve avantajlı algoritmadır

Naif sıralama: özet • Naif sıralama algoritmalar – Seçme sıralama – O(N 2) – Ekleme sıralama – O(N 2) – Kabarcık sıralama – O(N 2) • Naif sıralama algoritmalarının hepsi O(N 2) dır

Böl-ve-fethet sıralama • Hızlı sıralama algoritmaları – Hızlı sıralama (quicksort) – Birleşme sıralama (mergesort)

Hızlı sıralama (quicksort) • Ana fikri – Naif sıralama algoritması var, O(N 2) algoritmasıdır – Dizide bir sayı seçelim ( “pivot” denir), A – A’dan küçük sayıların hepsini sola koyalım, büyükleri sağa koyalım – Soldaki ve sağdaki sayılar ayrı olarak sıralayalım, sonra şöyle sıralanmış altdizileri birleştirelim (kolay çünkü soldakiler hepsi <A ve sağdakiler hepsi >A – yana konulması yeterlidir!)

Hızlı sıralama (quicksort) • Ana fikri – Sol dizi sadece A’dan daha küçük sayıları ve sağ dizi sadece A’dan daha büyük sayıları içerdiği için sol sıralanmış dizi solda sağ sıralanmış dizi sağda koyup hemen sıralanmış sonucu alıyoruz – Pivot olarak genellikle dizinin ortasındanki sayı seçilir

Hızlı sıralama (quicksort) • Zaman analizi: – Eğer altdizilerin sıralama naif olarak yapılırsa, toplam ortalama sıralama zamanı 2(N/2)2 + 1 ≈ N 2/2 – Yani zaten bu iki kat daha hızlı (ilginç değil mi)!

Hızlı sıralama (quicksort) • Zaman analizi: – Dolayısıyla, altdizileri sıralamak için aynı ikiye bölme yöntemi kullanalım, ve sayre – Sonuçta bu ikiye bölme yaklaşımı sona kadar kullanılırsa ortalama sıralama zamanı O(N log N) olmaktadır – Bu daha sonra konuşacağımız genel böl-ve-fethet algoritma yaklaşımının örneği dir

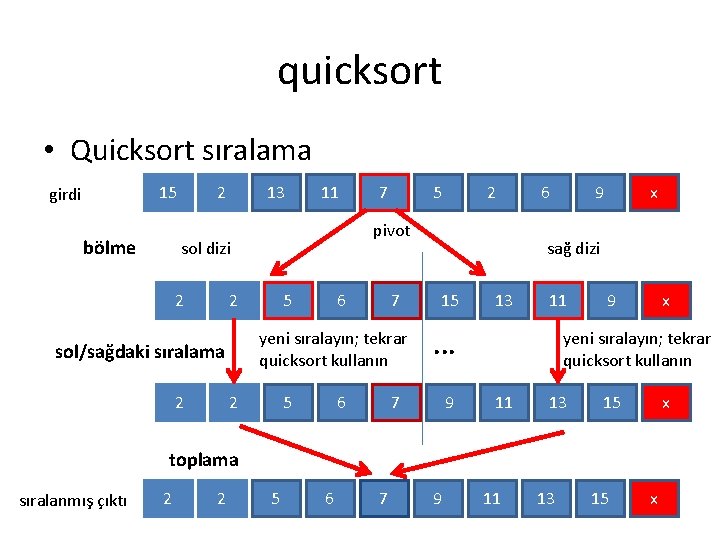
quicksort • Quicksort sıralama 15 girdi bölme 2 13 11 2 5 6 7 yeni sıralayın; tekrar quicksort kullanın sol/sağdaki sıralama 2 5 2 pivot sol dizi 2 7 2 5 6 6 9 x sağ dizi 15 13 11 . . . 7 9 9 x yeni sıralayın; tekrar quicksort kullanın 11 13 15 x toplama sıralanmış çıktı 2 2 5 6 7 9 11 13 15 x
![quicksort başlangıç quicksort p giriş dizi A porta soldiziboş dizi sağdiziboş dizi döngü i0dan quicksort başlangıç quicksort p: =giriş dizi A: =p[orta] sol_dizi=boş dizi sağ_dizi=boş dizi döngü i=0’dan](https://slidetodoc.com/presentation_image_h/acc04bc2c2b88712526408ec856a9da4/image-25.jpg)
quicksort başlangıç quicksort p: =giriş dizi A: =p[orta] sol_dizi=boş dizi sağ_dizi=boş dizi döngü i=0’dan p’nin boyutuna kadar eğer p[i]<A ise p[i] sol_diziye ekleyin aksi halde p[i] sağ_diziye ekleyin eğer sonu döngü sonu sol_dizi: =quicksort(sol_dizi); sağ_dizi: =quicksort(sağ_dizi); p: =(sol_dizi, sağ_dizi) yaz p seç A; sol=boş; sağ=boş; i=0; hair i++<boyut(p) evet p[i]<A hair evet p->sol sol=quicksort(sol); sağ=quicksort(sağ); [sol; sağ] bitiş p->sağ

quicksort • Quicksort sıralama için ortalama olarak O(N log N) zamandır gerekiyor • FAKAT, kötü pivot seçtiği ile O(N 2) zamana düşebilir

mergesort • Ana fikri – Naif sıralama algoritması var, O(N 2) algoritmasıdır – Quicksort’e benzeyen, ama sol ve sağ diziler için orijinal dizisini ortasından bölüyoruz, yani “pivot” kullanılmıyor – Sol ve sağ parçaları ayrı sıralanır, ama daha sonra biraz (çok az) daha karmaşık şekilde geri birleştirilir

mergesort • Ana fikri – Sol ve sağdaki dizilerde hem küçük hem büyük sayılar olabilir – Dolayısıyla sol ve sağ dizilerin birleştirmek için yana koymak yeterli değildir – Fakat şu lineer-zaman yaklaşım kullanılabilir

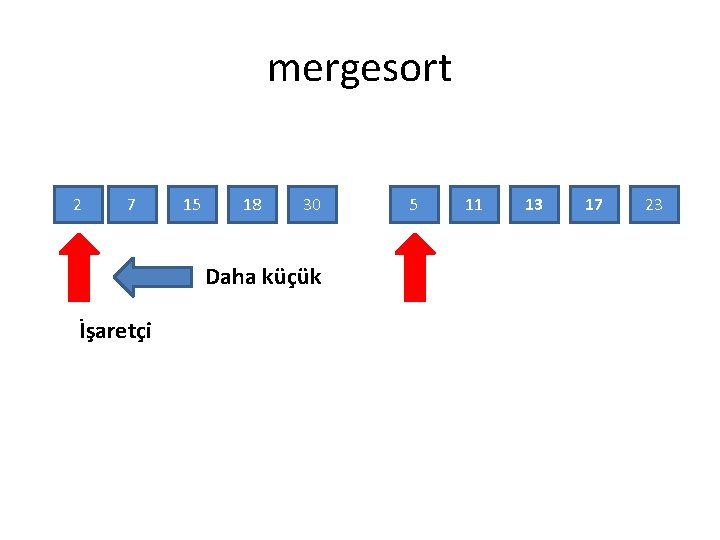
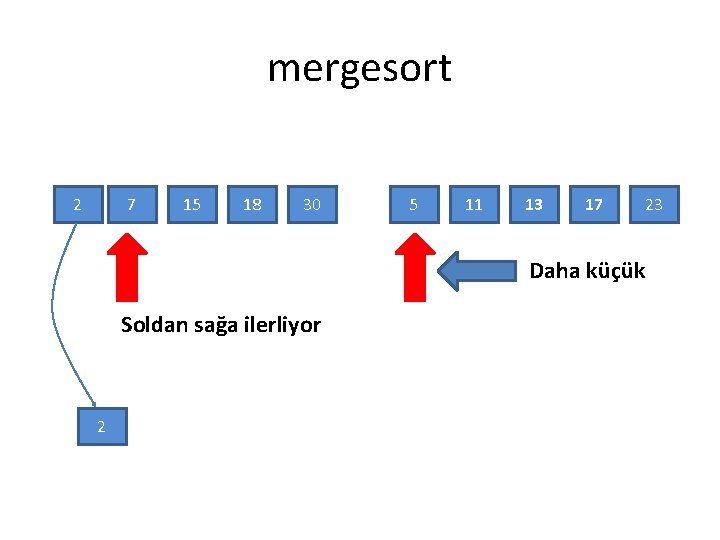
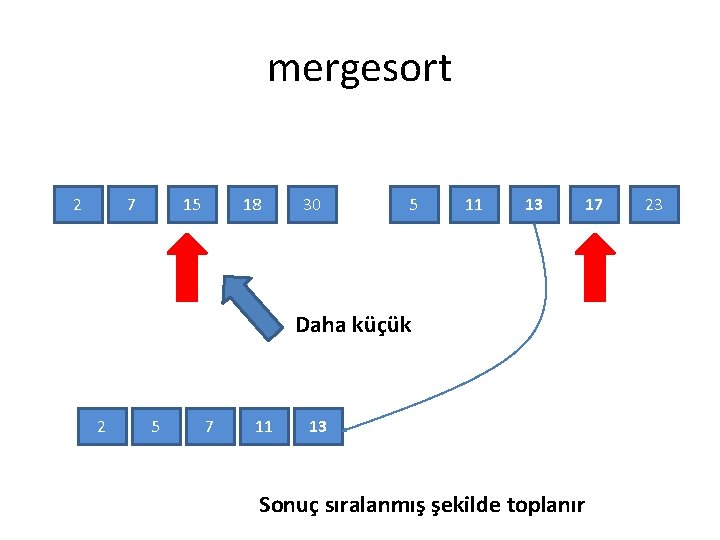
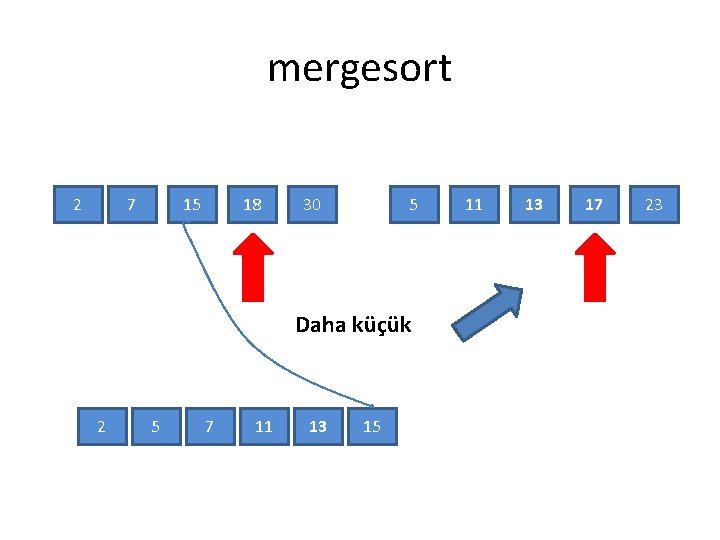
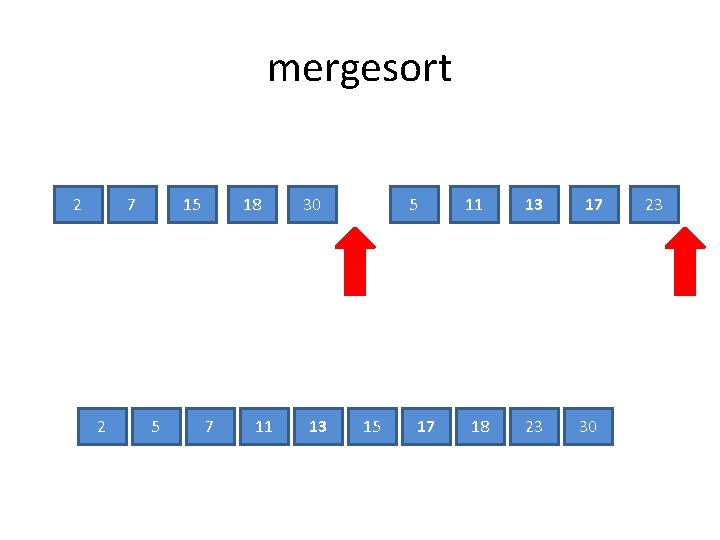
mergesort • Mergesort toplama algoritması: – Sağ ve sol altdizisinde soldan sağa giderken iki altdizisinden daha büyük olanı sonuç diziye ekliyoruz

mergesort 2 7 15 18 30 Daha küçük İşaretçi 5 11 13 17 23

mergesort 2 7 15 18 30 5 11 13 17 23 Daha küçük Soldan sağa ilerliyor 2

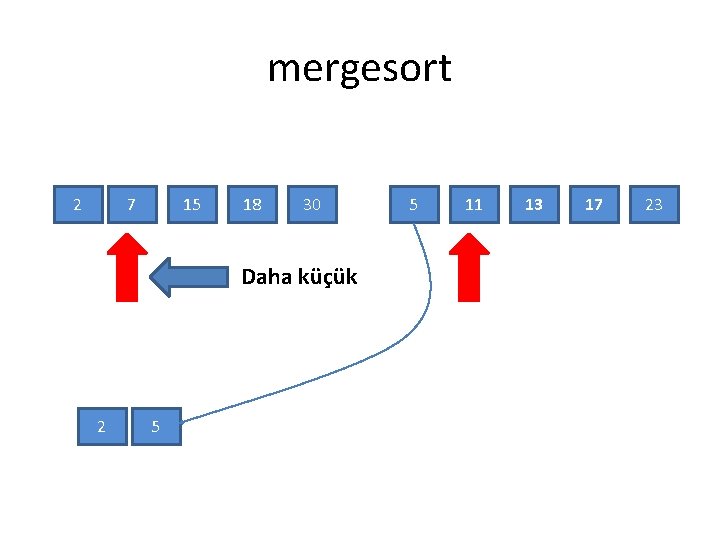
mergesort 2 7 15 18 30 Daha küçük 2 5 5 11 13 17 23

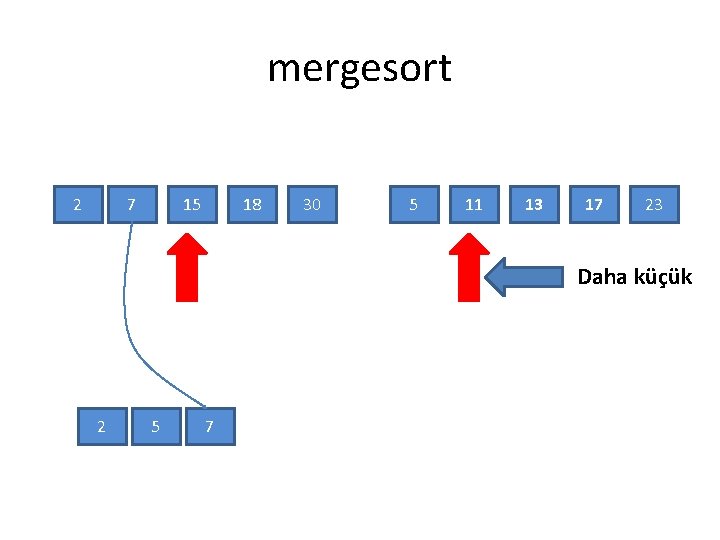
mergesort 2 7 15 18 30 5 11 13 17 23 Daha küçük 2 5 7

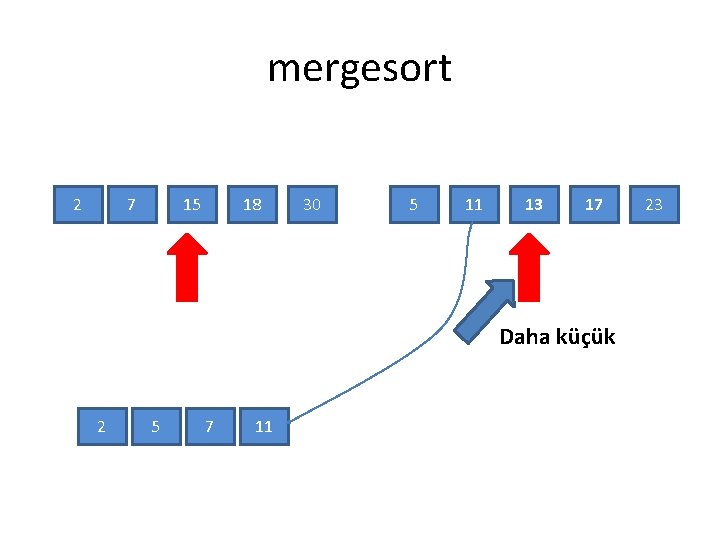
mergesort 2 7 15 18 30 5 11 13 17 Daha küçük 2 5 7 11 23

mergesort 2 7 15 18 30 5 11 13 17 Daha küçük 2 5 7 11 13 Sonuç sıralanmış şekilde toplanır 23

mergesort 2 7 15 18 30 5 Daha küçük 2 5 7 11 13 15 11 13 17 23

mergesort 2 7 2 15 5 18 7 11 30 13 5 15 17 11 18 13 23 17 30 23

mergesort • Quicksort sıralamanın tek adımla zaman kazanması şudur – Altsıralama zamanı – 2(N/2)2 – Birleştirme zamanı N – Toplam zamanı 2(N/2)2 +N – Yani, çok iyi

mergesort • Quicksort sıralama yeni O(N log N) zamanda yapılabilir, fakat burada en kötü durumun zamanı da O(N 2) zamandır ! • Mergesort sıralama, ortalama ve en kötü durumunda O(N log N) operasyon gerekiyor • Bu şekilde mergesoft optimal sıralama algoritmasıdır

heapsort • Bir daha O(N log N) önemli sıralama algoritması var – heapsort (hipsort) algoritması • Heapsort, böl-ve-fethet algoritması değildir, aslında “ekleme sıralama” algoritmalarından biridir

heapsort • Naif ekleme sıralamasında vakit gereksinimi O(N 2) idi, ama. . . • Ekleme operasyonunu daha akıllı şekilde yapacaksak daha verimli algoritma sağlanabilir – Ekleme ikiye bölme algoritması yada arama ağaçları kullanarak yapılırsa. . . – Ekleme işlemi O(log N) zamandır gerekir ve. . . – Dizi sıralama O(N log N) zamanda yapılacaktır

Sıralama Algoritmaları (Böl-ve-Fethet) • Naif sıralama algoritmaları – Seçme sıralama – O(N 2) – Ekleme sıralama – O(N 2) – Kabarcık sıralama – O(N 2) • Böl-ve-fethet sıralama algoritmaları – Quicksort sıralama – O(N log N) – Mergesort sıralama – O(N log N) • Sıralanmış veri yapıları algoritmaları – Heapsort sıralama – O(N log N)

Özel sıralama konuları • Tamsayım, kova ve radix özel sıralama algoritmaları var • O(N) (yani lineer) zaman algoritmalardır • Veritabanları için önemli algoritmalardır • Veritabanlarının indeksleri çoğunlukla tamsayılar olduğu için, bu algortima çok avantajlı gelir

Sayım sıralama • Ana fikri – Sayım sıralamada, orijinal dizideki tamsayılar sıralı şekilde incelenir ve o sayıların kaç kez karşılandığı takip edilir – Tüm dizi incelenince, bunlardan sonuç sıralanmış dizi oluşturulur

Sayım sıralama • Sayım sıralama 15 2 13 7 7 5 2 6 9 inceleme Karşılandığı sayı: "2" – 2 kez; "5" – 1 kez; "6" – 1 kez; "7" – 2 kez; "9" – 1 kez; "13" – 1 kez; "15" – 1 kez; Sonuç == (2, 2, 5, 6, 7, 7, 9, 13, 15) Bitti !

Sayım sıralama algoritması sayım: =boş dizi; // sayıların sayımları döngü i=0’dan p’nin uzunluguna kadar sayım[p[i]]: =sayım[p[i]]+1; // bütün sayılar için karşılandığı kezi not et döngü sonuç: =boş dizi; // sonuç döngü {"k" sayım’daki var olan indeksler için, en küçükten en büyüğe kadar} “k” sayı sonuç'a “sayım[k]” defa ekle; döngü sonu yaz p

Kova sıralama • Kova sıralama, sayım sıralamaya benzeyen bir yaklaşım • Dizide N sayı varsa, dizinin sayı aralığını N altaralığı/kovaya bölüyoruz, sonra. . . • Sayım sıralamada gibi, dizi sırayla inceliyoruz ve sayılar karşılık gelen kovaya ekliyoruz • Kovalardaki sayıları ayrı sıralanır ve kovaların sırasına göre sonuca birleştirilir

Kova sıralama • Ortalama, kovalar tek sayı içeriyor olacak (yani N sayı N kovaya bölünür), bu nedenle kova sıralama ortalama O(N) vakit gerekmektedir

Kova sıralama n: =p’nin boyutu kova: =n boş diziler; döngü i=0’dan n’ya kadar k: =p[i]’nin kovası p[i]->kova[k] döngü sonu döngü k=0’dan n’ya kadar kova[k]: =sırala(kova[k]) döngü sonuç: =boş dizi döngü k=0’dan n’ya kadar kova[k] -> sonuç döngü sonu yaz sonuç // n tane “kova” hazırlayın, kovaların hepsi // min(p) ve max(p) aralığının bir parçasıdır // sayıları karşılık gelen kovalara dağıtın // p[i] sayıyı karşılık gelen kovaya koyun // kovadaki sayıları sıralayın // kovaları, sırasına göre sonuca toplayın

Radix sıralama • Radix sıralama (basamak sıralaması) da bir tamsayı sıralama algoritmasıdır • Radix sıralamada, tamsayılar birkaç geçişte önce birinci basamaklarına göre sıralanıyor, sonra ikinci basamaklarına göre sıralanıyor, VB • Her bir geçiş sayım sıralama kullanarak yapılıyor – lineer zamanda

Radix sıralama • Radix sıralama O(KN) vakit gerekiyor, eğer K tamsayıların maksimum uzunluğu

Radix sıralama • İki tür var: “en anlamlı basamağa göre” ve “en anlamsız basamağa göre” türüleri var, bunlar tabi ya ilk yada son basamakla başlayan radix sıralama algoritmalardır

ilave sıralama konuları: radix sıralama Radix sıralama: girdi 15 02 13 11 07 05 02 06 09 Birinci geçiş 02 07 05 02 06 09 15 13 11 İkinci geçiş 02 02 05 06 07 09 11 13 15 birinci bölüm ikinci bölüm

Özet • Naif sıralama algoritmaları – Seçme sıralama – O(N 2) – Ekleme sıralama – O(N 2) – Kabarcık sıralama – O(N 2) • Böl-ve-fethet sıralama algoritmaları – Quicksort sıralama – O(N log N) – Mergesort sıralama – O(N log N) • Heapsort sıralama algoritması – İkiye bölme ekleme sıralama algoritması O(N log N)

Özet • Tamsayı sıralama algoritmaları – Sayım sıralama – Kova sıralama – Radix sıralama • Tamsayılar O(N) zamanda sıralanabilir • Veritabanları düzenlemesi için önemli avantajıdır

Böl-ve-fethet yaklaşımı • Böl-ve-fethet yaklaşımı, bügün gördüğümüz algoritma geliştirme bir esas genel yöntemidir

Böl-ve-fethet yaklaşımı • Böl-ve-fethet yaklaşımı, “kötü” yada “süperlineer zaman” bir algoritma varsa, uygulanabilir • Sorun birkaç altsorununa bölünür ve altsorunları ayrı "süperlineer zaman" yaklaşım yapılır • Bu algoritmanın süperlineer olduğundan dolayı böyle strateji ile avantaj kazanılır

Böl-ve-fethet yaklaşımı • Böl-ve-fethet’in ana fikri: • Bir sorun için bir algoritma var • Bu algoritma “kötü”, yani “N” büyüklüğınde olan sorunlar için N 2 yada daha çok zaman gerektiriyor (örneğin–naif sıralama) • Böyle durumlarda, süperlineer zaman algoritmanın var olduğunu diyoruz

Böl-ve-fethet yaklaşımı • Böl-ve-fethet’in ana fikri: • N büyüklüğünde olan sorundan birkaç yeni benzer daha küçük (örneğin 2 N/2 -altdizi sıralanması) altsorununu yapıyoruz ve bunları orijinal algoritmayı kullanıyoruz

Böl-ve-fethet yaklaşımı • Böl-ve-fethet yaklaşımının kullanılabilmesi için şöyle koşullar doğru olması lazım: 1. Problem çözme algoritma süperlineer olması lazım; 2. Orijinal problem altproblemlerine bölünebilmesi lazım; 3. Altproglemler orijnal probleme benziyor olması, yani aynı algoritma ile yapılabilmesi lazım; 4. Orijnal problemin çözümü altproblemlerinin çözümlerinden verimli olarak bulunabilmesi lazım.

Böl-ve-fethet yaklaşımı • Baze önemli kavramlar: • Problem çözme zaman gereksinimi, büyük N boyutta olan problemler için gereken çözme zamanı süperlineer, Ta(N)=O(Nk) • Altsonuçları birleştirme zaman gereksinimi, büyük N boyutta olan problemler için altsonuçları sonuca birleştirmek için gereken zaman – Tt(N)=O(N) (genellikle lineer)

Böl-ve-fethet yaklaşımı • Toplam vakit gereksinimi bu durumda şöyledir – 2*Ta(N/2)+Tt(N) • EĞER Ta(N/2)+Tt(N) < Ta(N) İSE, böl-vefethet yaklaşımı avantajlı görünüyor

Böl-ve-fethet yaklaşımı • Böl-ve-fethet yöntemin ünlü uygulamaları: • Hızlı Fourier Dönüşümü – Pratik uygulamalarda çok kullanılan, zaman sinyalinin frekansları hesaplama algoritmasıdır (frekans-dönüşümü) – Naif algoritma O(N 2) zamandır – Böl-ve-fethet algoritma O(N log N) zamandır • Sıralam – Sıralama naif algoritması O(N 2) zamandır – Böl-ve-fethet algoritma O(N log N) zamandır