Algorithms Lecture 5 DFSs Set psNULL and push

Algorithms Lecture 5

DFS(s) • Set p[s]=NULL and push s on stack S • While S is not empty do: – Pop node u from the top of S – If u is not marked explored • Mark u explored • For each edge (u, v) where v is not marked explored – Set p[v]=u and push v onto S // p[v] may be changed later • Running time O(|E|) when graph is given as adjacency list – Each edge considered at most once in each direction

Connectivity in directed graphs • Running BFS/DFS starting at s gives all the nodes that can be reached from s • Reversing the direction of all the edges and running BFS/DFS starting at s gives all the nodes that can reach s (in the original graph) • The strongly connected component containing s is the intersection of the two – Why?

Directed acyclic graphs (DAGs) • A directed graph with no cycles is called a DAG • Very common when encoding dependencies – E. g. , Boolean circuits, jobs, course prerequisites, … – If the dependency graph is not a DAG, there is no way to satisfy the dependencies

Topological ordering • A topological ordering of a directed graph is an ordering of the vertices such that all edges “go forward” (i. e. , from lower to higher index) – Not necessarily unique • Easy to see: if a graph has a topological ordering, then it is a DAG

Algorithmic problems • How to determine if a graph is a DAG? • If it is a DAG, does it have a topological ordering? If so, how to find one? • Key observation: – In a DAG there is a vertex with no ingoing edges • Otherwise, could continually follow edges backward and construct a cycle

Topological ordering • Corollary: Every DAG has a topological ordering! – Idea: put vertex v with no ingoing edges first, then compute topological ordering on V{v} • So a graph is a DAG iff it has a topological ordering • The above gives an algorithm for computing a topological ordering (if the graph is a DAG) – Repeatedly find v with no ingoing edges and place it next; update graph • O(|V|2) algorithm – Can we do better?

Topological ordering • Be less wasteful by using better book-keeping – For each vertex, maintain the number of ingoing edges in the current graph – Maintain set S of vertices with no ingoing edges – These can be initialized in O(|E|+|V|) time • Then in each iteration: – Take vertex v from S and place it next – For each edge (v, v’), decrement count of v’ and place v’ in S if applicable • O(|E|+|V|) time

Greedy algorithms

Greedy algorithms • Hard to formally define what a “greedy algorithm” is • Intuitively: try to optimize some criterion at every step – Optimize locally and hope that this leads to a global optimum • This will not always work! – But when it does, the resulting algorithm is often simple and efficient

Example: making change • Say we want to make a certain value v using the fewest number of coins – Available coins: 1, 5, 10, 25 • While v > 0 do: – Use largest coin c ≤ v – Set v = v-c

Making change • Does this always work? • Yes – if the coins are 1, 5, 10, 25 – Proof is not obvious! • What if we remove the nickel? – Running the greedy algorithm on v = 31 uses a quarter and 6 pennies 7 coins – Optimal is 3 dimes and a penny 4 coins • Whether the greedy algorithm is optimal or not depends on the denominations available

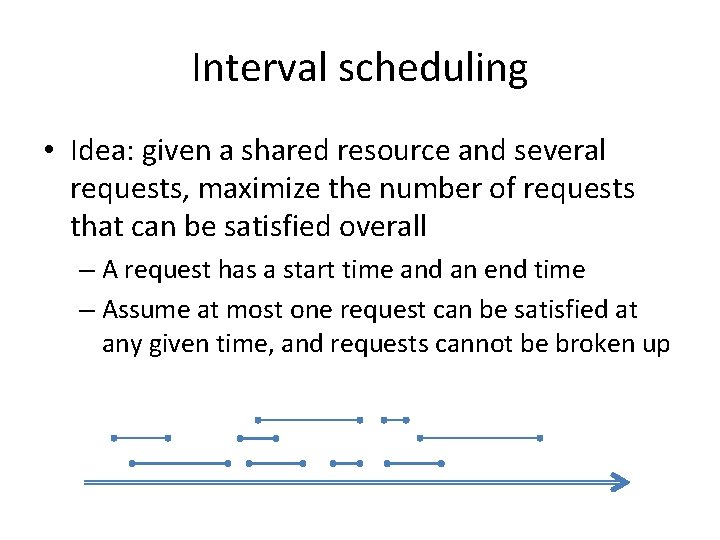
Interval scheduling

Interval scheduling • Idea: given a shared resource and several requests, maximize the number of requests that can be satisfied overall – A request has a start time and an end time – Assume at most one request can be satisfied at any given time, and requests cannot be broken up

Interval scheduling • Formally: – Request ri has the form (si, ei) with si < ei – Input: a set of requests T = {ri} – Output: T’ T of maximum size such that no distinct ri, rj T’ overlap • Overlap: si ≤ ej and ei ≥ sj

Template for greedy algorithm • // T is the set of requests currently under consideration; T’ is the set of requests we will satisfy • T’ = • While T is not empty do: – Pick some r T and add it to T’ – Update T by removing r and any requests that overlap with r from T • Note: this always produces a valid T’ – But may not be optimal

Some greedy ideas that don’t work • Always take the shortest request in T • Greedy algorithm satisfies 1 request, but optimal solution satisfies 2

Some greedy ideas that don’t work • Always take the request that overlaps the fewest other requests in T • Greedy algorithm satisfies 3 requests, but optimal solution satisfies 4

Greedy idea that works • Always take the request in T that ends earliest – Intuition: this leaves the resource available for the most time

Greedy idea that works • T’ = • While T is not empty do: – Pick r T that ends earliest and add it to T’ – Update T by removing r and any requests that overlap with r from T • Proof of correctness?

Proof of correctness • Fix some instance; let O be an optimal solution; let A be a set returned by the algorithm • Want to prove that |A| = |O| – Can’t hope to prove A = O; neither A nor O is necessarily unique

Proof of correctness • Order the requests in A and O – A = {a 1, a 2, …} – O = {o 1, o 2, …} • Claim: for all i, ai ends no later than oi • Proof: by induction – Clearly true for i=1 – Assume true for i • This means ai ends no later than oi • So oi+1 does not conflict with {a 1, …, ai} • If oi+1 ended before ai+1, then oi+1 would have been chosen instead of ai+1

Proof of correctness • Claim: |A|=|O| • Proof: – Assume not – Let A = {a 1, a 2, …, ak} and O = {o 1, o 2, …, ok+1, …} – By previous claim, ak ends no later than ok – But then ok+1 would have been added to A

Implementing the algorithm T’ = Sort requests in T by their ending times Initialize array S s. t. S[i] = start time of ri Set f=0 // assume the interval starts at 0 // f records the ending time of the requests in T’ • While i ≤ n: • • – Increment i until S[i] ≥ f – Add ri to T’; set f to the ending time of ri • Time O(n log n) overall (dominated by sorting)