AGT Towards the generalization of AGT relation KEK

AGT 関係式とその一般化に向けて (Towards the generalization of AGT relation) 高エネルギー加速器研究機構 (KEK) 素粒子原子核研究所 (IPNS) 柴　正太郎 (Shotaro Shiba) S. Kanno, Y. Matsuo, S. S. and Y. Tachikawa, Phys. Rev. D 81 (2010) 046004. S. Kanno, Y. Matsuo and S. S. , work in progress.

Introduction What is the multiple M-branes’ system like? (The largest motivation of my research) • The system of single M-brane in 11 -dim spacetime is understood, at least classically. • However, at this time, we have too little information on the multiple M-branes’ system. • Now I hope to understand more on M-theory by studying the internal degrees of freedom which the multiple branes’ systems must always have. Ø D-branes’ case : internal d. o. f ~ N 2 • The superstrings ending on a D-brane compose the internal d. o. f. • It is well known that this system is described by DBI action with gauge symmetry of Lie algebra U(N), which is reduced to Yang-Mills theory in the low-energy limit. 2

Ø M 2 -branes’ case : internal d. o. f. ~ N 3/2 • The proposition of BLG model is the important breakthrough. [Bagger-Lambert ’ 07] [Gustavsson ’ 07] • We can derive the internal d. o. f. of order N 3/2 naturally and successfully, using the finite representation of Lie 3 -algebra which is the gauge symmetry algebra of BLG model. [Chu-Ho-Matsuo-SS ’ 08] • However, at this moment, we don’t know at all what compose these d. o. f. Subject of today’s seminar Ø M 5 -branes’ case : internal d. o. f. ~ N 3 The near horizon geometry of M-branes is Ad. S x S, so we can use Ad. S/CFT discussion. Then this internal d. o. f. corresponds to the entropy of Ad. S blackhole. (~ area of horizon) Based on the recent research of AGT relation and its generalization, not a few researchers now hope that [Alday-Gaiotto-Tachikawa ’ 09] [Wyllard ’ 09] etc. • Toda fields on 2 -dim Riemann surface (or Seiberg-Witten curve [Seiberg-Witten ’ 94]) • W-algebra which is the symmetry algebra of Toda field theory bring us some new understanding on the multiple M 5 -branes’ internal d. o. f ! 3

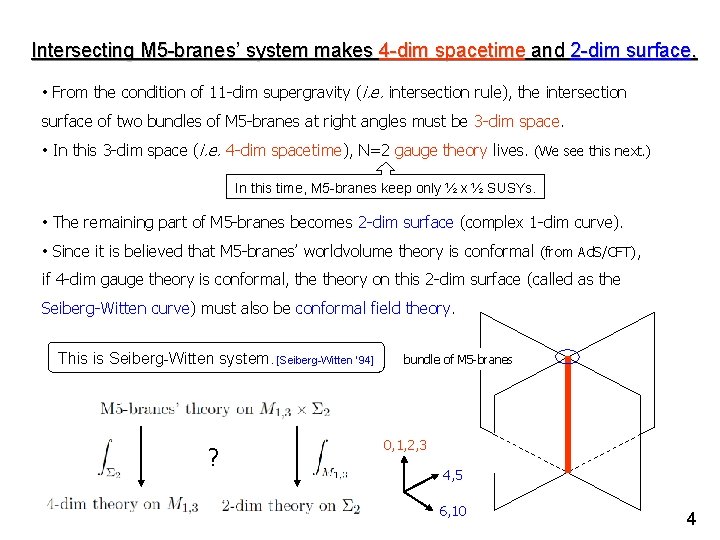
Intersecting M 5 -branes’ system makes 4 -dim spacetime and 2 -dim surface. • From the condition of 11 -dim supergravity (i. e. intersection rule), the intersection surface of two bundles of M 5 -branes at right angles must be 3 -dim space. • In this 3 -dim space (i. e. 4 -dim spacetime), N=2 gauge theory lives. (We see this next. ) In this time, M 5 -branes keep only ½ x ½ SUSYs. • The remaining part of M 5 -branes becomes 2 -dim surface (complex 1 -dim curve). • Since it is believed that M 5 -branes’ worldvolume theory is conformal (from Ad. S/CFT), if 4 -dim gauge theory is conformal, theory on this 2 -dim surface (called as the Seiberg-Witten curve) must also be conformal field theory. This is Seiberg-Witten system. [Seiberg-Witten ’ 94] ? bundle of M 5 -branes 0, 1, 2, 3 4, 5 6, 10 4

Seiberg-Witten curve determines the field contents of 4 -dim gauge theory. • Now we compactify 1 -dim space out of 11 -dim spacetime, and go to the D 4 -NS 5 system in superstring theory, since we have very little knowledge on M 5 -brane. • In string theory, (vibration modes) of F 1 -strings describe the gauge and matter fields. • The fields of this gauge theory are composed by F 1 -strings moving in 4 -dim spacetime. 4, 5 D 4 -brane (M 5 -brane) flavor brane color brane flavor brane (length = infinite) (length ~ 1/coupling) [Seiberg-Witten ’ 94] 6, 10 D 6 -brane 7, 8, 9 more generally… antifund. gauge bifund. F 1 -string gluons / quarks NS 5 -brane (M 5 -brane) increasing (from Hanany-Witten’s discussion) increasing • In general, gauge group is SU(d 1) x SU(d 2) x … x SU(N) x … x SU(d’ 2) x SU(d’ 1). This theory is conformal, when # of D 6 -branes is . 5

A kind of ‘deformations’ makes clear the structure of Seiberg-Witten curve. • To see the structure of Seiberg-Witten curve, now we move each D 4 -brane for longitudinal direction of NS 5 -branes to each distance. • After this ‘deformation’, the gauge fields get VEV’s, and the matter fields get masses. (This means, of course, that the gauge theory is no longer conformal. ) • In general cases, the Seiberg-Witten curve is described in terms of a polynomial as ~ direction of D 4　　 ~ direction of NS 5 Note that ü The coefficient of y N is 1. : normalization which causes the divergence of ! ü The y N-1 term doesn’t exist. : suitable shift of coordinates 6

Contents 1. Introduction (pp. 2 -6) 2. Gaiotto’s discussion 3. AGT relation (pp. 8 -10) (pp. 11 -17) 4. Towards proof of AGT relation (pp. 18 -22) 5. Towards generalized AGT relation 6. Conclusion (pp. 23 -29) (p. 30) 7

Gaiotto’s discussion Seiberg-Witten curve may be described by 2 -dim conformal field theory. When we recognize the intersecting point of D 4 -branes and NS 5 -branes as ‘punctures’, 2 -dim conformal field theory can be defined on Seiberg-Witten curve. NS 5 -branes 0 ∞ 0 [Gaiotto ’ 09] ∞ deformation to 2 -dim sphere multiple D 4 -branes 6 … d 3 – d 2 – d 1 … 10 (compactified) … … … 4, 5 … … d’ 3 – d’ 2 – d’ 1 (All Young tableaux are composed by N boxes. ) For gauge group : SU(d 1) x SU(d 2) x … x SU(N) x … x SU(d’ 2) x SU(d’ 1) 8

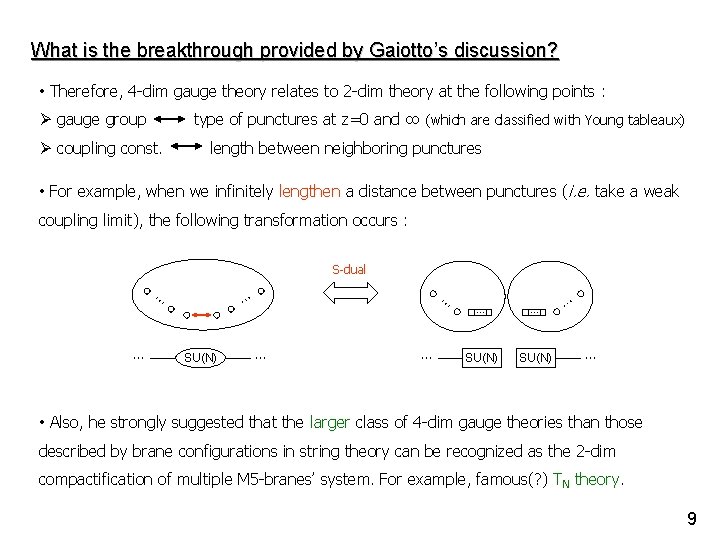
What is the breakthrough provided by Gaiotto’s discussion? • Therefore, 4 -dim gauge theory relates to 2 -dim theory at the following points : Ø gauge group 　　　　type of punctures at z=0 and ∞ (which are classified with Young tableaux) Ø coupling const. 　　　 length between neighboring punctures • For example, when we infinitely lengthen a distance between punctures (i. e. take a weak coupling limit), the following transformation occurs : S-dual … … … … SU(N) … … • Also, he strongly suggested that the larger class of 4 -dim gauge theories than those described by brane configurations in string theory can be recognized as the 2 -dim compactification of multiple M 5 -branes’ system. For example, famous(? ) TN theory. 9

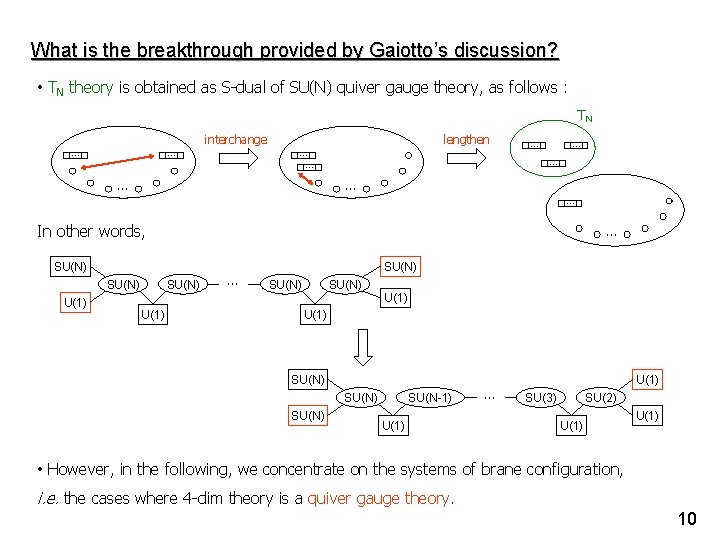
What is the breakthrough provided by Gaiotto’s discussion? • TN theory is obtained as S-dual of SU(N) quiver gauge theory, as follows : TN … … interchange lengthen … … … … In other words, … SU(N) U(1) SU(N) … SU(N) U(1) SU(N) SU(N-1) U(1) … U(1) SU(3) SU(2) U(1) • However, in the following, we concentrate on the systems of brane configuration, i. e. the cases where 4 -dim theory is a quiver gauge theory. 10

AGT relation reveals the concrete correspondence between partition function of 4 -dim SU(2) quiver gauge theory and correlation function of 2 -dim Liouville theory. Ø Action (Besides the classical part…) ü 1 -loop correction : more than 1 -loop is cancelled, because of N=2 supersymmetry. ü instanton correction : Nekrasov’s calculation with Young tableaux Ø Parameters (Sorry, they are different from Gaiotto’s ones!) ü coupling constants ü masses of fundamental / antifund. / bifund. fields and VEV’s of gauge fields link ü Nekrasov’s deformation parameters : background of graviphoton 11

1 -loop part of partition function of 4 -dim quiver gauge theory We can obtain it of the analytic form : gauge VEV where antifund. bifund. mass deformation parameters < Case of SU(N) x SU(N’) > : 1 -loop part can be written in terms of double Gamma function! 12

Instanton part of partition function of 4 -dim quiver gauge theory We obtain it of the expansion form of instanton number : where Young tableau : coupling const. and < Case of instanton # = 1 > + where (fractions of simple polynomials) 13

2. The correlation function of 2 -dim field theory • We put the (primary) vertex operators at punctures, and consider the correlation functions of them: • In general, the following expansion is valid: primaries descendants For the case of Virasoro algebra, , and e. g. for level-2, : Shapovalov matrix • It means that all correlation functions consist of 3 -point function and propagator , and the intermediate states (i. e. descendant fields) can be classified by Young tableaux. Ø Parameters (They correspond to parameters of 4 -dim gauge theory!) ü position of punctures ü momentum of vertex operators for internal / external lines ü central charge of the field theory 14

Correlation function of 2 -dim conformal field theory We obtain it of the factorization form of 3 -point functions and propagators : Ø 3 -point function where highest weight ~ simple punc. Ø propagator (2 -point function) : inverse Shapovalov matrix 15

AGT relation : SU(2) gauge theory Liouville theory ! [Alday-Gaiotto-Tachikawa ’ 09] Ø 4 -dim theory : SU(2) quiver gauge theory Ø 2 -dim theory : Liouville (SU(2) Toda) field theory In this case, the 4 -dim theory’s partition function Z and the 2 -dim theory’s correlation function correspond each other : Gauge theory Liouville theory coupling const. 　　　 position of punctures VEV of gauge fields momentum of internal lines mass of matter fields momentum of external lines 1 -loop part DOZZ factors instanton part conformal blocks deformation parameters 　 Liouville parameters central charge : 16

Natural expectation : SU(N>2) gauge theory SU(N) Toda theory… !? Ø 4 -dim theory : SU(N) quiver gauge theory [Wyllard ’ 09] [Kanno-Matsuo-SS-Tachikawa ’ 09] Ø 2 -dim theory : SU(N) Toda field theory • Similarly, we want to study on correspondence between partition function of 4 -dim theory and correlation function of 2 -dim theory : • This discussion is somewhat complicated, since in these cases, punctures are classified with more than one kinds of Young tableaux (which composed by N boxes) : < full-type > < simple-type > < other types > … … … … (cf. In SU(2) case, all these Young tableaux become ones of the same type . ) 17

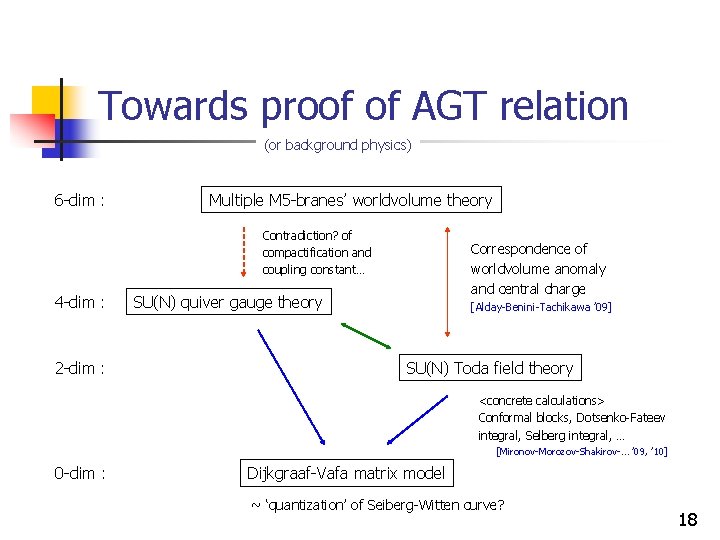
Towards proof of AGT relation (or background physics) 6 -dim : Multiple M 5 -branes’ worldvolume theory Contradiction? of compactification and coupling constant… 4 -dim : 2 -dim : Correspondence of worldvolume anomaly and central charge SU(N) quiver gauge theory [Alday-Benini-Tachikawa ’ 09] SU(N) Toda field theory <concrete calculations> Conformal blocks, Dotsenko-Fateev integral, Selberg integral, … [Mironov-Morozov-Shakirov-… ’ 09, ’ 10] 0 -dim : Dijkgraaf-Vafa matrix model ~ ‘quantization’ of Seiberg-Witten curve? 18

Existence of Toda fields? : multiple M 5 -branes’ worldvolume anomaly First, we remember how the anomaly is cancelled in the single M 5 -brane’s case. For example, [Berman ’ 07] for a review. ü worldvolume fields : bosons (5 d. o. f. ) / fermions (8 d. o. f. ) / self-dual 2 -form field (3 d. o. f. ) ü inflow mechanism (interaction term in the 11 -dim supergravity action at 1 -loop level in l p) : ü Chern-Simons interaction (which needs careful treatment because of presence of M 5 -branes) : Therefore, when we naively consider, in the case of (multiple) N M 5 -branes’ case, x. N Cancellation doesn’t work!! (T_T) x N 3 It is believed that this is an indication of some extra fields on M 5 -branes’ worldvolume : 19

Existence of Toda fields? : multiple M 5 -branes’ worldvolume anomaly • This story is related to AGT relation, if we compactify M 5 -branes’ worldvolume on 4 -dim [Alday-Benini-Tachikawa ’ 09] space X 4. We define 2 -dim anomaly by integrating I 8 over X 4: • On the spacetime symmetry, we consider the following situation: TW NW • We twist R 5 over X 4 so that N=2 supersymmetry on X 4 remains. In this case, N=(0, 2) supersymmetry with U(1) R-symmetry remains on . The general form of anomaly is F : external U(1) bundle coupling to U(1)R symmetry • Especially, in the case of with Nekrasov’s deformation , (from AGT relation) This is precisely the same as central charge of Toda theory! 20

Toda theory is quantum theory of SW curve? : Dijkgraaf-Vafa matrix model • We consider 4 -dim and 2 -dim system in type IIB string theory. [Dijkgraaf-Vafa ’ 09] ü 4 -dim : Topological strings on Calabi-Yau 3 -fold ü 2 -dim : Seiberg-Witten curve embedded in Calabi-Yau 3 -fold • Dijkgraaf-Vafa matrix model may provide a bridge between them. ü matrix model is powerful tool of description of topological B-model strings. ü matrix model is also related to Liouville and Toda systems (, as we will see concisely). • Concretely, the partition function of 4 -dim theory and the correlation function of 2 -dim theory may be connected via the partition function of matrix model : where , 21

Toda theory is quantum theory of SW curve? : Dijkgraaf-Vafa matrix model • It is known that the free fermion system ( ) can describe the system of creation and annihilation of D-branes which are extended, for example, as • To define this system, we ‘quantize’ Seiberg-Witten curve as , so the following chiral path integral must be given naturally : • On the other hand, it is known that x classically act on fermions as • To sum up, in ‘quantum’ theory, x may be represented as • This means that an additional term is given in chiral path integral : When we bosonize the fermions, this additional term is nothing but the Toda potential ! 22

Towards generalized AGT relation • In the previous section, we saw some evidence(? ) that Toda fields live on Seiberg. Witten curve or multiple M 5 -branes’ worldvolume. • Now let us return the discussion on generalization of AGT relation. To do this, we need to consider… ü momentum of Toda fields in vertex operators : Again, in SU(N>2) case, we need to determine the form of vertex operators which corresponds to each kind of punctures (classified with Young tableaux). ü how to calculate the conformal blocks of W-algebra: 3 pt functions and propagators ü correspondence between parameters of SU(N) quiver gauge theory and those of SU(N) Toda field theory 23

What is SU(N) Toda field theory? : some extension of Liouville field theory • In this theory, there are energy-momentum tensor and higher spin fields as Noether currents. • The symmetry algebra of this theory is called W-algebra. • For the simplest example, in the case of N=3, the generators are defined as And, their commutation relation is as follows: For simplicity, we ignore Toda potential (interaction) at this present stage. which can be regarded as the extension of Virasoro algebra, and where 　　　　　　 , 24

As usual, we compose the primary, descendant, and null fields. • The primary fields are defined as　　　　　　　, so the descendant fields are composed by acting / 　 on the primary fields as uppering / lowering operators. • First, we define the highest weight state as usual : Then we act lowering operators on this state, and obtain various descendant fields as • However, (special) linear combinations of descendant fields accidentally satisfy the highest weight condition. Such states are called null states. For example, the null states in level-1 descendant fields are • As we will see next, we found the fact that this null state in W-algebra is closely related to the singular behavior of Seiberg-Witten curve near the punctures. That is, Toda fields whose existence is predicted by AGT relation may describe the form (or behavior) of Seiberg-Witten curve. 25

The singular behavior of SW curve is related to the null fields of W-algebra. [Kanno-Matsuo-SS-Tachikawa ’ 09] • As we saw, Seiberg-Witten curve is generally represented as ~ direction of D 4　 ~ direction of NS 5 and Laurent expansion near z=z 0 of the coefficient function is generally • This form is similar to Laurent expansion of W-current ( i. e. definition of W-generators) • Also, the coefficients satisfy the similar equation, except the full-type puncture’s case null condition This correspondence becomes exact, when we take some ‘classical’ limit : (which is related to Dijkgraaf-Vafa’s discussion on free fermion’s system? ) • This fact strongly suggest that vertex operators corresponding non-full-type punctures must be the primary fields which has null states in their descendant fields. 26

The punctures on SW curve corresponds to the ‘degenerate’ fields! • If we believe this suggestion, we can conjecture the form of momentum of Toda field [Kanno-Matsuo-SS-Tachikawa ’ 09] in vertex operators , which corresponds to each kind of punctures. • To find the form of vertex operators which have the level-1 null state, it is useful to define the screening operator (a special type of vertex operator) • We can easily show that the state satisfies the highest weight condition, since the screening operator commutes with all the W-generators. (Note that the screening operator itself has non-zero momentum. ) • This state doesn’t vanish, if the momentum satisfies for some j. In this case, the vertex operator has a null state at level . 27

The punctures on SW curve corresponds to the ‘degenerate’ fields! • Therefore, when we write the simple root as the condition of level-1 null state becomes (as usual), for some j. • It means that the general form of mometum of Toda fields satisfying this null state condition is . Note that this form naturally corresponds to Young tableaux . • More generally, the null state condition can be written as (The factors are abbreviated, since they are only the images under Weyl transformation. ) • Moreover, from physical state condition (i. e. energy-momentum is real), we need to choose Here, , instead of naive generalization of Liouville case . is the same form of β, is Weyl vector, and . 28

Our plans of current and future research on generalized AGT relation Ø Case of SU(3) quiver gauge theory ü SU(3) : already checked successfully. [Wyllard ’ 09] [Mironov-Morozov ’ 09] ü SU(3) x … x SU(3) : We checked 1 -loop part, and now calculate instanton part. ü SU(3) x SU(2) : We check it now, but correspondence seems very complicated! Ø Case of SU(4) quiver gauge theory • In this case, there are punctures which are not full-type nor simple-type. • So we must discuss in order to check our conjucture (of the simplest example). • The calculation is complicated because of W 4 algebra, but is mostly streightforward. Ø Case of SU(∞) quiver gauge theory • In this case, we consider the system of infinitely many M 5 -branes, which may relate to Ad. S dual system of 11 -dim supergravity. • Ad. S dual system is already discussed using LLM’s droplet ansatz, which is also governed by Toda equation. [Gaiotto-Maldacena ’ 09] 29

Conclusion n It is well known that Seiberg-Witten system can be regarded as the multiple M 5 branes’ system. This system is composed by intersecting M 5 -branes, and can be described by (direct sum? of) 4 -dim quiver gauge theory and 2 -dim conformal field theory on Seiberg-Witten curve. n Recently, it was strongly suggested that the partition function of 4 -dim theory and the correlation function of 2 -dim theory closely correspond to each other. In particular, this correspondence requires that Toda (or Liouville) field should live in 2 -dim theory on Seiberg-Witten curve. n We showed that the singular behavior of SW curve near punctures corresponds to the composition of null states in W-algebra. Also, we conjectured the momentum of vertex operators corresponding each kind of punctures. n Again, we expect that this subject brings us new understanding on M 5 -branes! 30