A Review of Some INVARIANCE PRINCIPLES Hermitian Operators























- Slides: 28

A Review of Some INVARIANCE PRINCIPLES Hermitian Operators: R† = R • can be diagonalized Unitary Operators: R† = R-1 • have real eigenvalues • define the physical observables • represent transformations of basis (vectors/functions) • can transform operators & wavefunctions by similarity transformations that leave the Lagrangian (and therefore the equations of motion) invariant. (include rotations/translations) A A = RAR† and =R so that all computed matrix elements: < | A| > = < | A | > = < |R†(RAR†)R| > = < |A| > Furthermore: If the Hamiltonian is unchanged by the similarity transformation i. e. if RHR† =H then RH = HR [H, R] = 0 and the eigenvalues are constants of the equations of motion, i. e. , we have conserved quantities

If Both Hermitian and Unitary: R†R = R-1 R = R 2 = 1 R has eigenvalue of 1 this also implies: det(R) = det(I) = 1 det(R) = 1 We’ve focussed a lot on the special det(R)=+1 cases: simple SO(n) rotations SU(n) • These are “continuous symmetries”: seamlessly connected to the identity matrix I by infinitesimal transformations • expressible by exponential sums of infinitesimal transformations • such operators can be used to define a CURRENT that obeys the continuity equation • which we can identify with an associated CHARGE

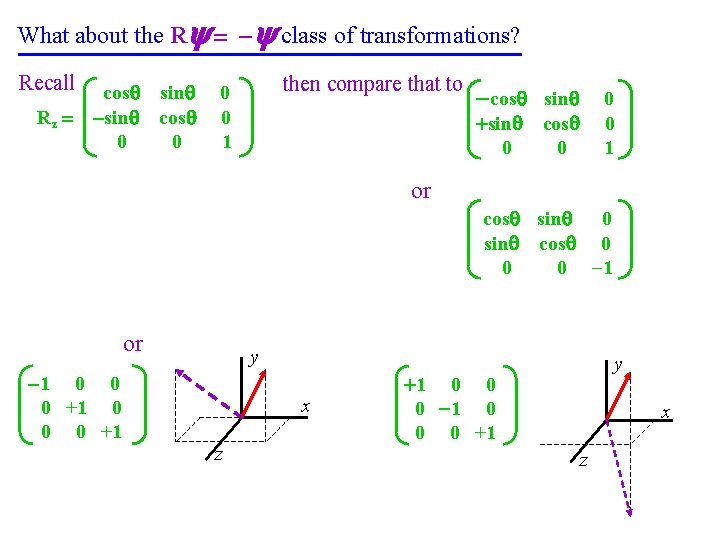
What about the R = - class of transformations? Recall Rz = cos sin -sin cos 0 0 then compare that to 0 0 1 -cos sin +sin 0 cos 0 0 0 1 or cos sin 0 sin cos 0 0 0 -1 or -1 0 0 0 +1 y x z y +1 0 0 0 -1 0 0 0 +1 x z

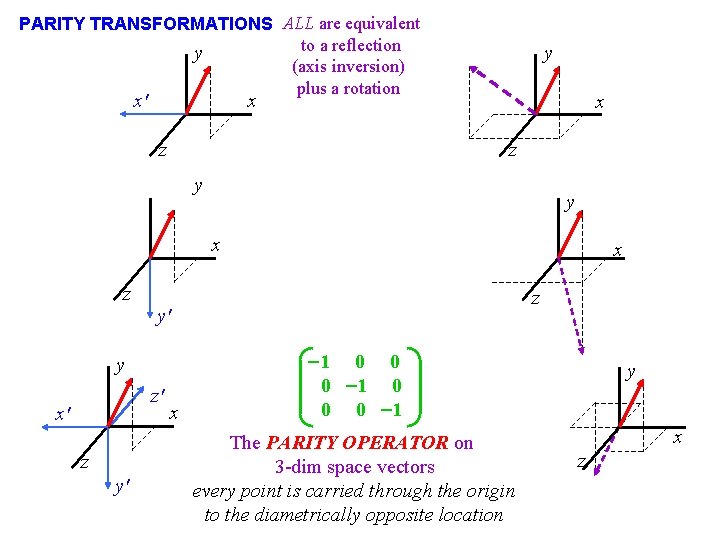
PARITY TRANSFORMATIONS ALL are equivalent to a reflection y (axis inversion) plus a rotation x' y x z y y x z z' z y' y x' x x -1 0 0 0 -1 The PARITY OPERATOR on 3 -dim space vectors every point is carried through the origin to the diametrically opposite location y x z

Wave functions MAY or MAY NOT have a well-defined parity (even or odd functions…or NEITHER) P P = +1 P P = -1 but the more general P

However for any spherically symmetric potential, the Hamiltonian: → → H(-r) = H(r) [ P, H ] = 0 So they bound states of such a system have DEFINITE PARITY! That means, for example, all the wave functions of the hydrogen atom!

Y(r)=c(r) ml ( , ) m l( , ) = the angular part of the solutions are the SPHERICAL HARMONICS (2 l + 1)( l- m)! m P l (cosq)eim 4 ( l + m)! Pml (cosq) = (-1)msinmq [( d d (cos ) 1 d Pl (cosq) = l [( d (cos ) 2 l! )m Pl (cosq)] )l (-sin 2 q)l ]

The Spherical Harmonics Yℓ, m( , ) ℓ=0 ℓ=1 ℓ=2 ℓ=3

z then note r -r means p- q p-q p + y so: eimfeimp x (eip)m=(-1)m and: Pml (cos ) Pml (cos(p- )) = Pml (-cos ) (-sin 2 q)l = (-1 -cos 2 q)l but d/d(cosq) - d/d(cosq)

m l( , ) = (2 l + 1)( l- m)! m im P (cosq)e l 4 ( l + m)! d Pml (cosq) = (-1)m(1 -cos 2 q)m [( d (cos ) 1 d Pl (cosq) = l [( d (cos ) 2 l! )m Pl (cosq)] )l (-sin 2 q)l ] So under the parity transformation: P: ml ( , ) = ml (p- , p+ )=(-1)l(-1)m ml ( , ) = (-1)l(-1)2 m ml ( , ) )=(-1)l ml ( , ) An atomic state’s parity is determined by its angular momentum l=0 l=1 l=2 (s-state) (p-state) (d-state) constant cos (3 cos 2 -1) parity = +1 parity = -1 parity = +1 Spherical harmonics have (-1)l parity.

When acting on a vector, the parity operator gives: P P scalars have positive parity! P ? ? ? This confusion arises from the indefinite nature of cross products… their direction is DEFINED by a convention…the right-hand rule. and reflections (parity!) change right hands left hands! We call such derived/defined vectors PSEUDO-VECTORS (or “axial” vectors) → as opposed to POLAR VECTORS, like v.

QUANTITY PARITY Comments r p -r -p L +L + E B -E +B • B • E • p + • B - • E - • p position momentum polar vectors angular momentum intrinsic “spin” axial or pseudovectors electric field E = - V/ r B = ×A pseudo-vector magnetic dipole moment electric dipole moment longitudinal polarization • (p 1×p 2) + • (p 1×p 2) transverse polarization

Potential problems with this concept…or assuming its invariance… Lot’s of physics uses Right Hand Rules and cross-products… angular momentum has POSITIVE parity the Lorentz Force Law vectors! Just like you can’t add vectors to scalars, cannot (should not try) to add vectors and pseudovectors at least for any theory that should respect parity invariance

But notice a vector crossed with a pseudo-vector: P where is a vector! Might B really be a pseudo-vector quantity after all? → the “vector” potential is a true vector! and as we have argued in quantum mechanics/high energy theory is the more fundametnal field!

In our Lagrangians we identify the currents as vectors. Of particular interest: → → J • A of electromagnetic interactions → J is a vector → A is a vector field i. e. , the photon is a vector particle with “odd” parity! So electromagnetic interactions conserve parity. By the same argument QCD Color (the STRONG force) interactions …its Lagrangian terms all involve inner products of all 4 -vectors… conserve parity!

A mono-chromatic electromagnetic wave is composed of n mono-energetic photons each with In addition to energy and momentum light (the photon) also carries angular momentum (its spin!)

1909 Poynting predicts circularly polarized electromagnetic waves carry angular momentum proposes a test: if incident upon an absorber, the absorber should rotate 1936 Richard Beth detects the angular momentum of light transferred to matter. photon momentum transferred to a “half-wave plate”, a macroscopic object hung on a fiber (but with a non-vanishing torsion constant). R. A. Beth Phys. Rev. 50, 115 (1936).

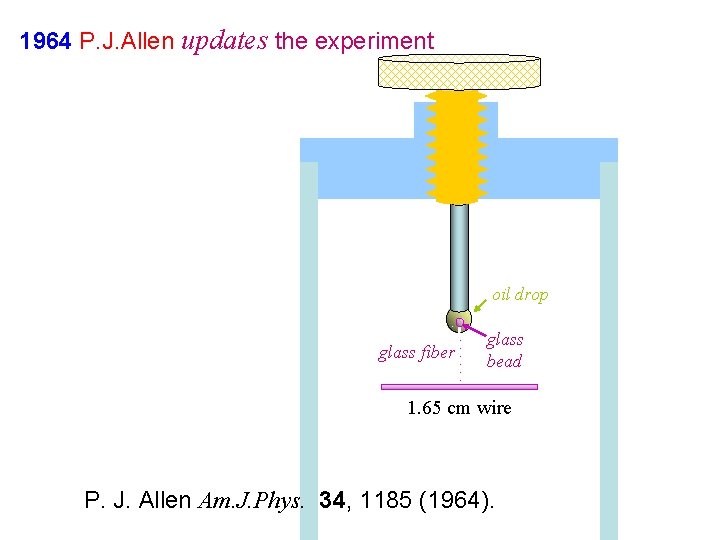
1964 P. J. Allen updates the experiment oil drop glass fiber glass bead 1. 65 cm wire P. J. Allen Am. J. Phys. 34, 1185 (1964).

Microwave generator beamed up cavity sets rotor in motion E = LZ If delivered by n photons, then E = nħ with means LZ = n j. Z = ħ Each photon has spin 1.

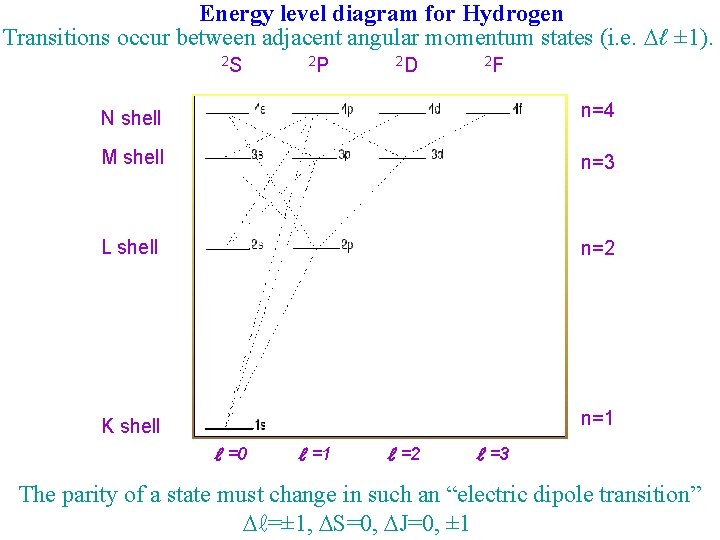
Energy level diagram for Hydrogen Transitions occur between adjacent angular momentum states (i. e. ℓ ± 1). 2 S 2 P 2 D 2 F N shell n=4 M shell n=3 L shell n=2 K shell n=1 ℓ =0 ℓ =1 ℓ =2 ℓ =3 The parity of a state must change in such an “electric dipole transition” ℓ=± 1, S=0, J=0, ± 1

s, d, g, … even parity p, f, h, … odd parity The atomic transitions responsible for the observed atomic spectra connect these states of different parity. When the atomic state changes, PARITY must be conserved. The ELECTRIC DIPOLE transitions (characterized by ℓ ± 1) emit PHOTONS whose parity must therefore be NEGATIVE.

Like s which can be singly emitted (created) or absorbed (annihilated) s are created/destroyed singly in STRONG INTERACTIONS Their “INTINSIC PARITY” is also important. To understand the role of parity in interactions, consider a system (let’s start with a single pair of particles) of initially free (non-interacting) which we can describe as a product state: large P parity is a multiplicative quantum number If the pair is bound with orbital angular momentum P

If P commutes with both the free particle Hamiltonian and the full Hamiltonian with interactions the (parity) quantum numbers are conserved throughout the interactions which is obviously true for electromagnetic interactions strong interactions since the Lagrangian terms incorporating these interactions are all invariant under P

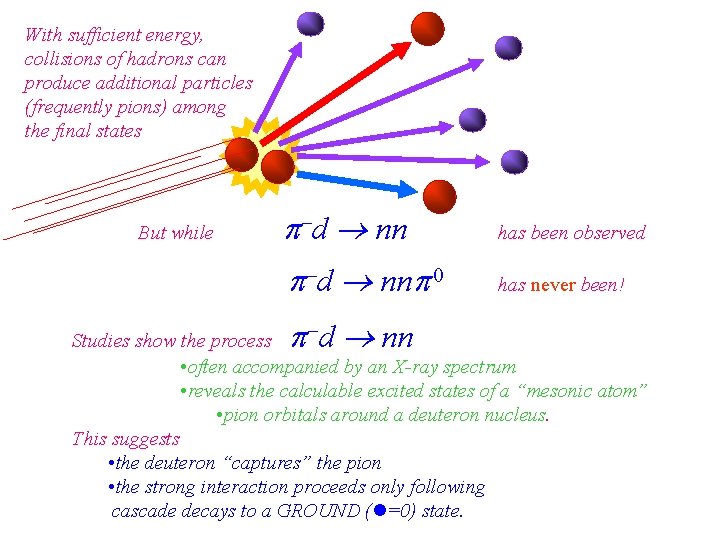
With sufficient energy, collisions of hadrons can produce additional particles (frequently pions) among the final states But while p-d nn has been observed p-d nnp 0 has never been! p d nn Studies show the process • often accompanied by an X-ray spectrum • reveals the calculable excited states of a “mesonic atom” • pion orbitals around a deuteron nucleus. This suggests • the deuteron “captures” the pion • the strong interaction proceeds only following cascade decays to a GROUND ( =0) state.

p-d nn An =0 ground state means the p d system has J = Stotal =? 1 So the final nn state must also have J = 1? =1 =0 =1 =2 s=0 s=1 s=1 Note the final state is 2 Dirac FERMIONS overall wave function must be ANTISYMMETRIC to particle exchange Space part described by the spherical harmonics (interchanging the neutrons would reverse their relative positions, i. e. r -r P : (r, , )=(-1) (r, , ) Spin part ? s=1 s=1 s=0 ms = 1 ms = 0 ms = -1 ms = 0

p-d nn Space part Spin part ? P : (r, , )=(-1) (r, , ) s=1 s=1 s=0 ms = + 1 ms = 0 ms = -1 ms = 0 P +1 under exchange P -1 under exchange

p-d nn Space part Spin part ? P : (r, , )=(-1) (r, , ) s=1 s=1 s=0 So overall must have ms = + 1 ms = 0 1/ 2( + ms = -1 ms = 0 1/ 2( (-1) +s+1 = -1 +s even =1 =0 =1 =2 s=0 s=1 s=1 ) ) P +1 under exchange P -1 under exchange =(-1)s+1 (-1) +s = +1 Thus the parity of the final nn system Must be (-1) = -1

p-d nn Since strong interactions conserve parity we must also have P: p-d = -1 d is a bound np s-state (-1) Pp. Pp =(+1)(+1) so P: p-d = (-1) =0 Pp. Pd = (+1)Pp(+1) Pp = -1
 3x3 orthogonal matrix
3x3 orthogonal matrix Example of an orthogonal matrix
Example of an orthogonal matrix Invariance property
Invariance property Fourier transform amplitude and phase
Fourier transform amplitude and phase Semtools measurement invariance
Semtools measurement invariance Bilinear transformation example
Bilinear transformation example Equivariance vs invariance
Equivariance vs invariance Is sinx acceptable wave function
Is sinx acceptable wave function Contoh soal fungsi eigen
Contoh soal fungsi eigen What is momentum operator
What is momentum operator Matriks antisimetris
Matriks antisimetris They say it only takes a little faith to move a mountain
They say it only takes a little faith to move a mountain They say sometimes you win some
They say sometimes you win some The ice cream is countable or uncountable
The ice cream is countable or uncountable Contact force
Contact force Some say the world will end in fire some say in ice
Some say the world will end in fire some say in ice Some say the world will end in fire some say in ice
Some say the world will end in fire some say in ice Some may trust in horses
Some may trust in horses Chapter review motion part a vocabulary review answer key
Chapter review motion part a vocabulary review answer key Uncontrollable spending ap gov
Uncontrollable spending ap gov Nader amin-salehi
Nader amin-salehi Prisma diagram example
Prisma diagram example Narrative review vs systematic review
Narrative review vs systematic review Arithmetic operators in vbscript
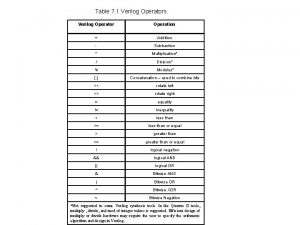
Arithmetic operators in vbscript Verilog operator
Verilog operator Shorthand assignment operator
Shorthand assignment operator Relational operators
Relational operators Quantum mechanics postulate
Quantum mechanics postulate Class operators public static void main
Class operators public static void main