Invariance Principles in Theoretical Computer Science Ryan ODonnell





![Learning Theory Servedio’ 08] Thm : [O- Can learn LTFs f in poly(n) time, Learning Theory Servedio’ 08] Thm : [O- Can learn LTFs f in poly(n) time,](https://slidetodoc.com/presentation_image/2c945dab63515725b593fa110941ff91/image-6.jpg)
![Property Testing Servedio’ 09] Thm : [Matulef-O-Rubinfeld- Can test if ϵ-close to an LTF Property Testing Servedio’ 09] Thm : [Matulef-O-Rubinfeld- Can test if ϵ-close to an LTF](https://slidetodoc.com/presentation_image/2c945dab63515725b593fa110941ff91/image-7.jpg)
![Derandomization Zuckerman’ 10] Thm : [Meka- PRG for LTFs with seed length O(log(n) log(1/ Derandomization Zuckerman’ 10] Thm : [Meka- PRG for LTFs with seed length O(log(n) log(1/](https://slidetodoc.com/presentation_image/2c945dab63515725b593fa110941ff91/image-8.jpg)

![Derandomization+ Zuckerman’ 10] Thm : [Gopalan-O-Wu- PRG for “functions of O(1) LTFs” with seed Derandomization+ Zuckerman’ 10] Thm : [Gopalan-O-Wu- PRG for “functions of O(1) LTFs” with seed](https://slidetodoc.com/presentation_image/2c945dab63515725b593fa110941ff91/image-10.jpg)
![Property Testing+ [Blais -O’ 10] Thm : Testing if Majority of k bits needs Property Testing+ [Blais -O’ 10] Thm : Testing if Majority of k bits needs](https://slidetodoc.com/presentation_image/2c945dab63515725b593fa110941ff91/image-11.jpg)
![Social Choice, Inapproximability Oleszkiewicz’ 05] Thm : [Mossel-O- a) Among voting schemes where no Social Choice, Inapproximability Oleszkiewicz’ 05] Thm : [Mossel-O- a) Among voting schemes where no](https://slidetodoc.com/presentation_image/2c945dab63515725b593fa110941ff91/image-12.jpg)




![Niceness of random variables Say E[X] = 0, stddev[ X] = σ. def : Niceness of random variables Say E[X] = 0, stddev[ X] = σ. def :](https://slidetodoc.com/presentation_image/2c945dab63515725b593fa110941ff91/image-17.jpg)
![Niceness of random variables Say E[X] = 0, stddev[ X] = σ. def : Niceness of random variables Say E[X] = 0, stddev[ X] = σ. def :](https://slidetodoc.com/presentation_image/2c945dab63515725b593fa110941ff91/image-18.jpg)











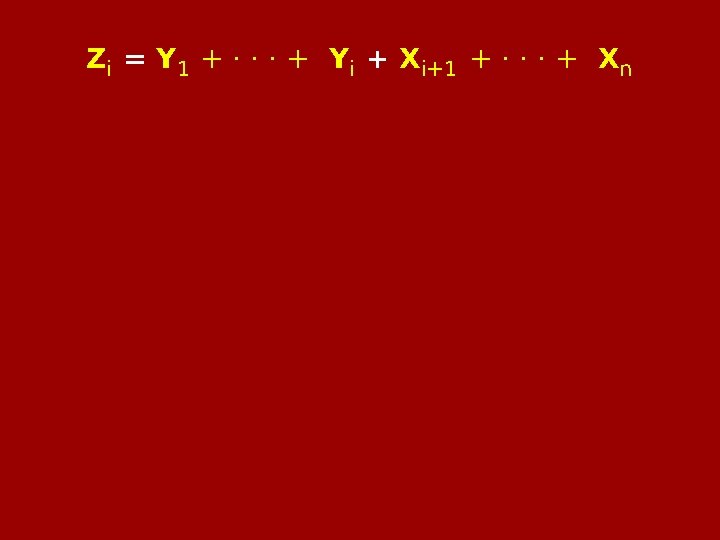








- Slides: 41

Invariance Principles in Theoretical Computer Science Ryan O’Donnell Carnegie Mellon University

Talk Outline 1. Describe some TCS results requiring variants of the Central Limit Theorem. 2. Show a flexible proof of the CLT with error bounds. 3. Open problems and an advertisement.

Talk Outline 1. Describe some TCS results requiring variants of the Central Limit Theorem. 2. Show a flexible proof of the CLT with error bounds. 3. Open problems and an advertisement.

Linear Threshold Functions

Linear Threshold Functions
![Learning Theory Servedio 08 Thm O Can learn LTFs f in polyn time Learning Theory Servedio’ 08] Thm : [O- Can learn LTFs f in poly(n) time,](https://slidetodoc.com/presentation_image/2c945dab63515725b593fa110941ff91/image-6.jpg)
Learning Theory Servedio’ 08] Thm : [O- Can learn LTFs f in poly(n) time, just from correlations Key: when all |c i | ≤ ϵ. E[f( x)xi ].
![Property Testing Servedio 09 Thm MatulefORubinfeld Can test if ϵclose to an LTF Property Testing Servedio’ 09] Thm : [Matulef-O-Rubinfeld- Can test if ϵ-close to an LTF](https://slidetodoc.com/presentation_image/2c945dab63515725b593fa110941ff91/image-7.jpg)
Property Testing Servedio’ 09] Thm : [Matulef-O-Rubinfeld- Can test if ϵ-close to an LTF with poly(1/ Key: when all |c i | ≤ ϵ. ϵ) querie
![Derandomization Zuckerman 10 Thm Meka PRG for LTFs with seed length Ologn log1 Derandomization Zuckerman’ 10] Thm : [Meka- PRG for LTFs with seed length O(log(n) log(1/](https://slidetodoc.com/presentation_image/2c945dab63515725b593fa110941ff91/image-8.jpg)
Derandomization Zuckerman’ 10] Thm : [Meka- PRG for LTFs with seed length O(log(n) log(1/ ϵ)). Key: even when xi ’s not fully independent.

Multidimensional CLT? For when all small compared to
![Derandomization Zuckerman 10 Thm GopalanOWu PRG for functions of O1 LTFs with seed Derandomization+ Zuckerman’ 10] Thm : [Gopalan-O-Wu- PRG for “functions of O(1) LTFs” with seed](https://slidetodoc.com/presentation_image/2c945dab63515725b593fa110941ff91/image-10.jpg)
Derandomization+ Zuckerman’ 10] Thm : [Gopalan-O-Wu- PRG for “functions of O(1) LTFs” with seed length O(log(n) log(1/ Key: ϵ)). Derandomized multidimensional CLT.
![Property Testing Blais O 10 Thm Testing if Majority of k bits needs Property Testing+ [Blais -O’ 10] Thm : Testing if Majority of k bits needs](https://slidetodoc.com/presentation_image/2c945dab63515725b593fa110941ff91/image-11.jpg)
Property Testing+ [Blais -O’ 10] Thm : Testing if Majority of k bits needs k is a Ω(1) queries. Key: assuming E[Xi ] = E[Yi ], Var[ Xi ] = Var[ Yi ], and some other conditions. (actually, a multidimensional version)
![Social Choice Inapproximability Oleszkiewicz 05 Thm MosselO a Among voting schemes where no Social Choice, Inapproximability Oleszkiewicz’ 05] Thm : [Mossel-O- a) Among voting schemes where no](https://slidetodoc.com/presentation_image/2c945dab63515725b593fa110941ff91/image-12.jpg)
Social Choice, Inapproximability Oleszkiewicz’ 05] Thm : [Mossel-O- a) Among voting schemes where no voter has unduly large influence, Majority is most robust to noise. b) Max-Cut is UG-hard to. 878 -approx. Key: If P is a low-deg. multilin. polynomial, assuming P has “small coeffs. on each coord. ”

Talk Outline 1. Describe some TCS results requiring variants of the Central Limit Theorem. 2. Show a flexible proof of the CLT with error bounds. 3. Open problems and an advertisement.

Gaussians Standard Gaussian: G ~ N(0, 1). Mean 0, Var Anti-concentration: Pr[ G ∈ [u− ϵ, u+ ϵ] ] ≤ O a + b G also a “Gaussian”: N(a, b 2) Sum of independent Gaussians is Gaussian: If G ~ N(a, b 2 ), H ~ N(c, d 2 ) are independen then G + H ~ N(a+c, b 2 +d 2 ).

Central Limit Theorem (CLT) X 1 , X 2 , X 3 , … independent, ident. distrib. , mean 0, variance σ 2,

CLT with error bounds X 1 , X 2 , …, Xn independent, ident. distrib. , mean 0, variance 1/n, X 1 + · · · + Xn is “close to” N(0, 1), assuming Xi is not too wacky:
![Niceness of random variables Say EX 0 stddev X σ def Niceness of random variables Say E[X] = 0, stddev[ X] = σ. def :](https://slidetodoc.com/presentation_image/2c945dab63515725b593fa110941ff91/image-17.jpg)
Niceness of random variables Say E[X] = 0, stddev[ X] = σ. def : ( ≥ σ). “ def ”: X is “ nice ” if eg : not nice : ± 1. N(0, 1). Unif on [-a, a].
![Niceness of random variables Say EX 0 stddev X σ def Niceness of random variables Say E[X] = 0, stddev[ X] = σ. def :](https://slidetodoc.com/presentation_image/2c945dab63515725b593fa110941ff91/image-18.jpg)
Niceness of random variables Say E[X] = 0, stddev[ X] = σ. def : ( def : eg : not nice : ≥ σ). X is “ C-nice ” if ± 1. N(0, 1). Unif on [-a, a].

Berry-Esseen Theorem X 1 , X 2 , …, Xn independent, ident. distrib. , mean 0, variance 1/n, X 1 + · · · + Xn is ϵ-close to N(0, 1), assuming Xi is C-nice , where [Shevtsova’ 07]: Y “ ϵ-close” to Z: . 7056

General Case X 1 , X 2 , …, Xn independent, ident. distrib. , mean 0, X 1 + · · · + Xn is ϵ-close to N(0, 1), assuming Xi is C-nice ,

Berry-Esseen: How to prove? X 1 , X 2 , …, Xn indep. , mean 0, S = X 1 + · · · + Xn ϵ-close to G ~ N(0, 1). 1. “Characteristic functions” 2. “Stein’s method” 3. “Replacement” = think like a cryptographer

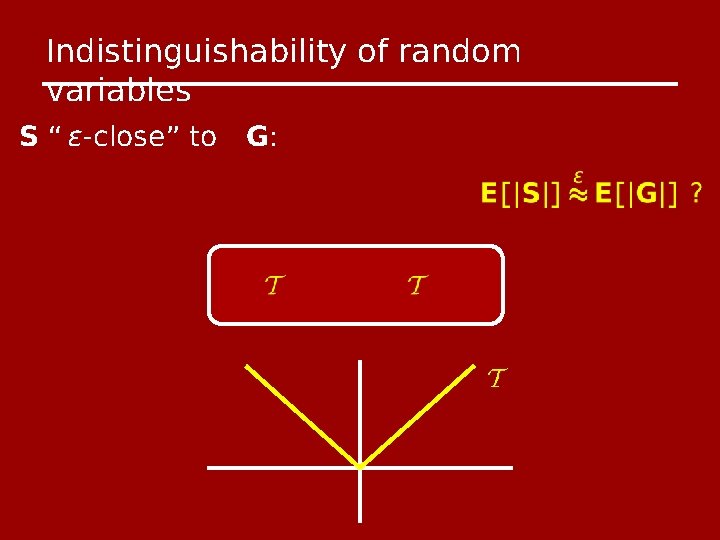
Indistinguishability of random variables S “ ϵ-close” to G:

Indistinguishability of random variables S “ ϵ-close” to G: u

Indistinguishability of random variables S “ ϵ-close” to G: t u

Indistinguishability of random variables S “ ϵ-close” to G:

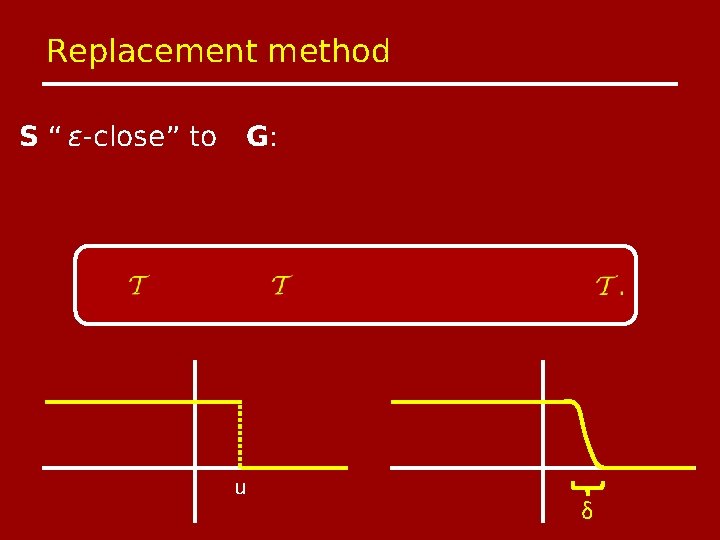
Replacement method S “ ϵ-close” to G: u δ

Replacement method X 1 , X 2 , …, Xn indep. , mean 0, S = X 1 + · · · + Xn G ~ N(0, 1) For smooth

Replacement method Hybrid argument X 1 , X 2 , …, Xn indep. , mean 0, S = X 1 + · · · + Xn G = G 1 + · · · + Gn For smooth

Invariance principle X 1 , X 2 , …, Xn Y 1 , Y 2 , …, Yn indep. , mean 0, Var[ Xi ] = Var[ Yi ] = SX = X 1 + · · · + X n S Y = Y 1 + · · · + Yn For smooth

Hybrid argument X 1 , X 2 , …, Xn , Y 1 , Y 2 , …, Yn , independent matching means and variances. SX = X 1 + · · · + Xn vs. SY = Y 1 + · · · + Yn Def : Zi = Y 1 + · · · + Yi + Xi+1 + · · · + Xn S X = Z 0 , S Y = Zn

Hybrid argument X 1 , X 2 , …, Xn , Y 1 , Y 2 , …, Yn , independent matching means and variances. Zi = Y 1 + · · · + Yi + Xi+1 + · · · + Xn Goal:
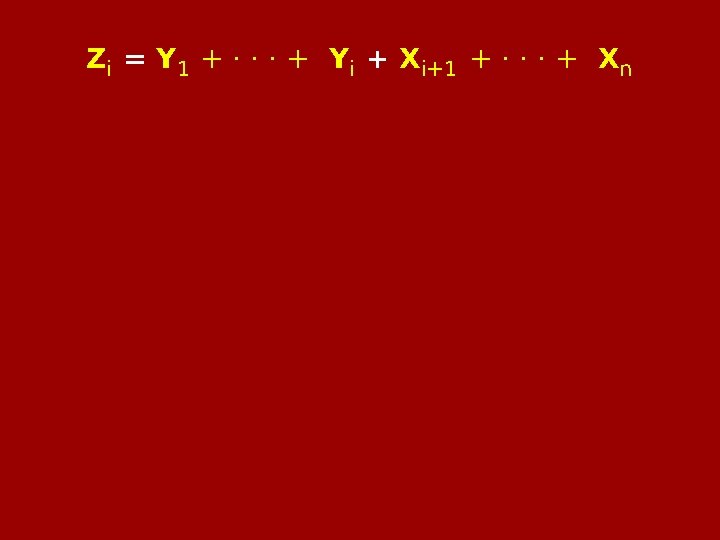

Zi = Y 1 + · · · + Yi + Xi+1 + · · · + Xn where U = Y 1 + · · · + Yi− 1 + Xi+1 + · · · + Xn Note: U, Xi , Yi independent. Goal:

− = ∴ by indep. and matching means/variances!

Variant Berry-Esseen: Say If X 1 , X 2 , …, Xn & Y 1 , Y 2 , …, Yn indep. and have matching means/variances, then

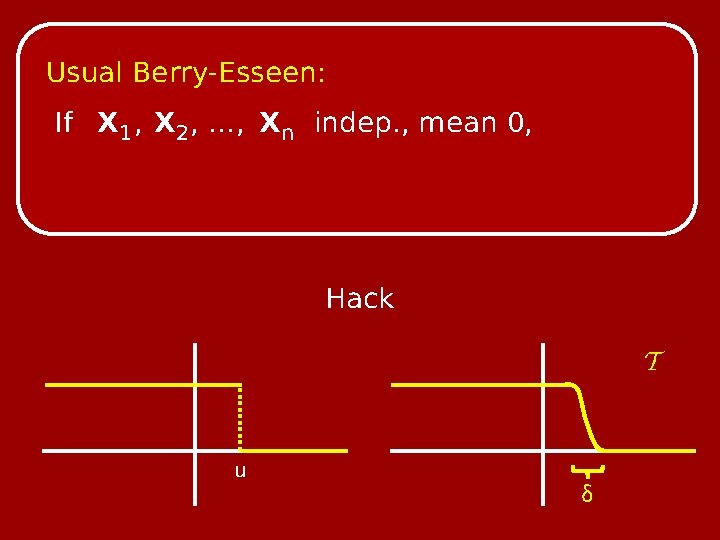
Usual Berry-Esseen: If X 1 , X 2 , …, Xn indep. , mean 0, Hack u δ

Usual Berry-Esseen: If X 1 , X 2 , …, Xn indep. , mean 0, Variant Berry-Esseen + Hack Usual Berry-Esseen except with error O( ϵ 1/4 )

Extensions are easy! Vector-valued version: Use multidimensional Taylor theorem. Derandomized version: If X 1 , …, Xm C-nice, 3 -wise indep. , then X 1 +···+ Xm is O(C)-nice. Higher-degree version: X 1 , …, Xm C-nice, indep. , Q is a deg. -d poly. , then Q( X 1 , …, Xm ) is O(C) d -nice.

Talk Outline 1. Describe some TCS results requiring variants of the Central Limit Theorem. 2. Show a flexible proof of the CLT with error bounds. 3. Open problems, advertisement, anecdote?

Open problems 1. Recover usual Berry-Esseen via the Replacement method. 2. Vector-valued: Get correct dependence on test sets K. ( Gaussian surface area 3. Higher-degree: improve (? ) the exponential dependence 4. Find more applications on degree d. in TCS. ? )

Do you like LTFs and PTFs ? Do you like probability and geometry ? Oct. 21 -22 (“ just before FOCS ”) workshop at the Princeton Intractability Center: Analysis and Geometry of Boolean Threshold Functions Diakonikolas! Kane! Meka! Rubinfeld! Servedio! Shpilka! Vempala! And more! http: //intractability. princeton. edu/blog/2010/08/workshop-ltfptf/