A matrix generation approach for eigenvalue optimization Mohammad

A matrix generation approach for eigenvalue optimization Mohammad R. Oskoorouchi California State University San Marcos, CA, USA International Conference on Continuous Optimization Rensselaer Polytechnic Institute August 2 – 4, 2004

Outline: • • Eigenvalue optimization From optimization to feasibility Weighted analytic center Recovering feasibility • Adding a p-dimensional matrix • Adding a column • Computational experience. • Future extensions

Eigenvalue optimization: Consider the following optimization problem:

Maximum eigenvalue function: • Continuous • Convex • nondifferentiable • nonpolyhedral cone • Cannot be written as the point-wise maximum of finite number of convex smooth function

The objective function can be cast as a semidefinite program: Now let be a feasible point and the maximum eigenvalue of has multiplicity , and be a matrix whose columns form a basis for the eigenspace for the maximum eigenvalue. By restricting to a subcone generated at the query point, we obtain a lower bound for

Let us study the inequality closely: or more

is represented by where

• is a compact convex set with nonempty interior, composed of linear and semidefinite inequalities. • contains the optimal solution set • is referred to as the set of localization

Weighted Analytic Center The weighted analytic is defined as the maximizer of the weighted dual potential function:

The primal formulation The weighted analytic center can be alternatively derived by the weighted primal potential function:

KKT optimality conditions

Approximate analytic centers

The primal directions:

Projection to the primal null space: This condition may not satisfy due to the computational round-off error. We therefore project the primal directions back to the primal null space.

Lemma

Recovering feasibility: So far, we reformulated the eigenvalue optimization problem into a convex feasibility problem, and derived a query point as an approximate analytic center of the set of localization: The eigenvalue function is evaluated at this point and there are two cases:

Adding a p-dimensional matrix: If f is not differentiable at the query point y, an oracle returns a subgradient of f at this point. The subgradient is in the form of semidefinite inequality and will be used to update the set of localization. Dual set of localization will be updated via

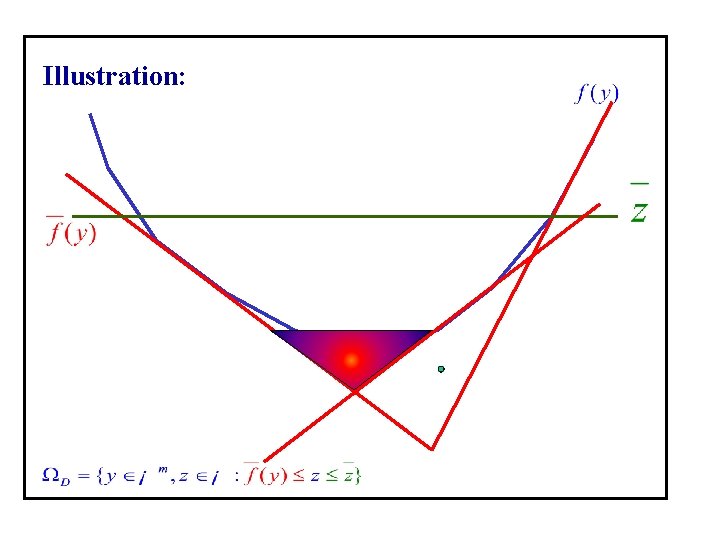
Illustration:

Primal set of localization: Due to computational difficulties with the deep cuts, in practice we use the primal set to recover centrality. We now need a strictly feasible point for the updated primal set of localization.

Primal updating direction: Implementing Newton method, one has

Primal updating direction: The objective function of this problem is composed of a quadratic term and a self-concordant function. Therefore, Newton method is suitable to solve this problem:

Primal updating direction: The Newton step d. T is obtained by setting the gradient of F(T+d. T) with respect to d. T to zero:

Adding a column:

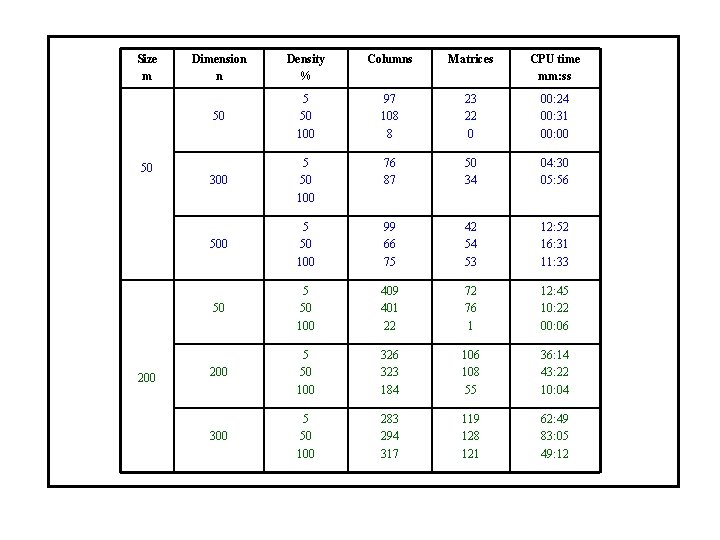
Size m 50 200 Dimension n Density % Columns Matrices CPU time mm: ss 50 5 50 100 97 108 8 23 22 0 00: 24 00: 31 00: 00 300 5 50 100 76 87 50 34 04: 30 05: 56 500 5 50 100 99 66 75 42 54 53 12: 52 16: 31 11: 33 50 5 50 100 409 401 22 72 76 1 12: 45 10: 22 00: 06 200 5 50 100 326 323 184 106 108 55 36: 14 43: 22 10: 04 300 5 50 100 283 294 317 119 128 121 62: 49 83: 05 49: 12

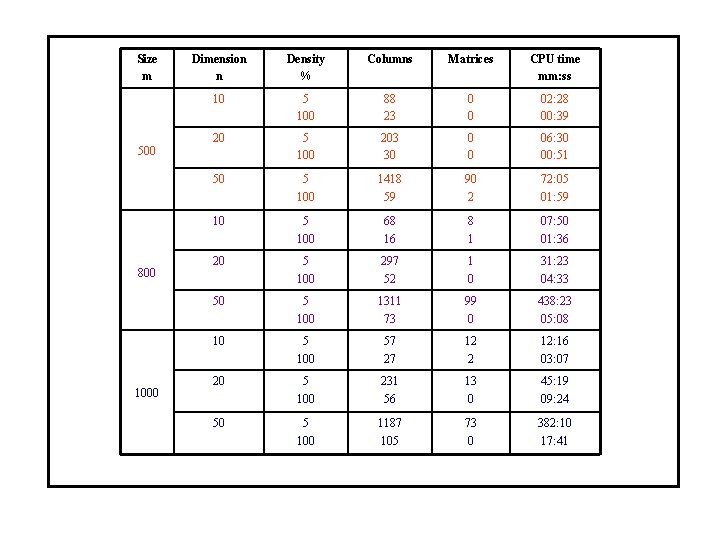
Size m 500 800 1000 Dimension n Density % Columns Matrices CPU time mm: ss 10 5 100 88 23 0 0 02: 28 00: 39 20 5 100 203 30 0 0 06: 30 00: 51 50 5 100 1418 59 90 2 72: 05 01: 59 10 5 100 68 16 8 1 07: 50 01: 36 20 5 100 297 52 1 0 31: 23 04: 33 50 5 100 1311 73 99 0 438: 23 05: 08 10 5 100 57 27 12 2 12: 16 03: 07 20 5 100 231 56 13 0 45: 19 09: 24 50 5 100 1187 105 73 0 382: 10 17: 41