A Dynamical Model of Molecular Monolayers Why Tethers

A Dynamical Model of Molecular Monolayers: Why Tethers Don’t Snap? Lu Zou, * Violeta Beleva, * Andrew J. Bernoff, # James C. Alexander, + J. Adin Mann Jr. ! Elizabeth K. Mann* *Dept. of Physics, Kent State University # Dept. of Mathematics, Harvey Mudd College + Dept of Mathematics, Case Western Reserve University ! Dept of Chemical Engineering, Case Western Reserve University 1

Relaxation of 8 CB on Water/Air Interface Why Don’t Tethers Snap? 2

OVERVIEW • Introduction on Rayleigh instability (3 D) and Hele-Shaw flow (2 D) • A dynamic model of molecular monolayers (2 D) • Simulation and experimental results • Conclusion and prospects 3

Rayleigh Instability [1878] • Pure, cylindrical 3 D fluid • Varicose mode fluctuations • Decrease area/surface energy • Break into droplets 4

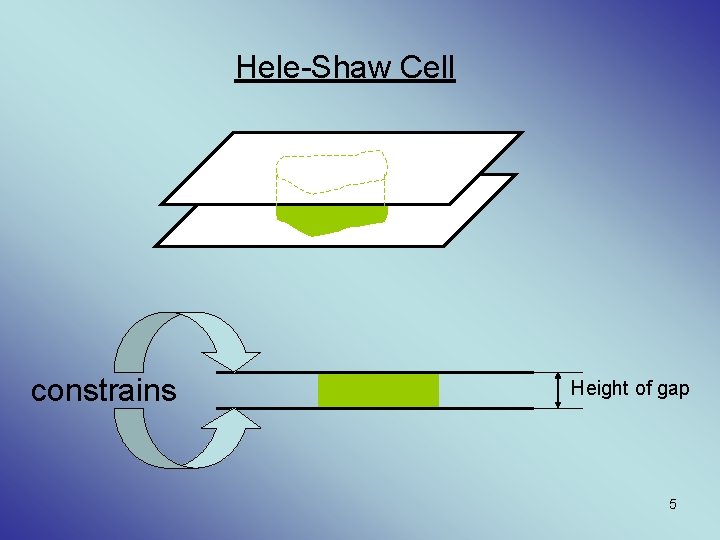
Hele-Shaw Cell constrains Height of gap 5

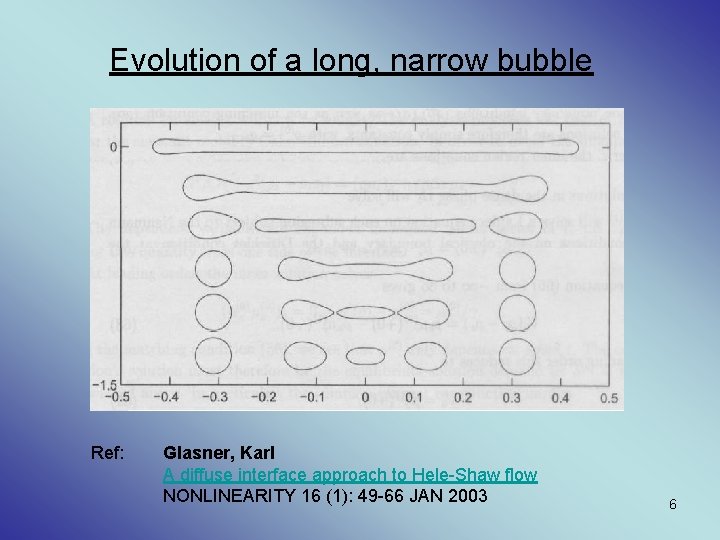
Evolution of a long, narrow bubble Ref: Glasner, Karl A diffuse interface approach to Hele-Shaw flow NONLINEARITY 16 (1): 49 -66 JAN 2003 6

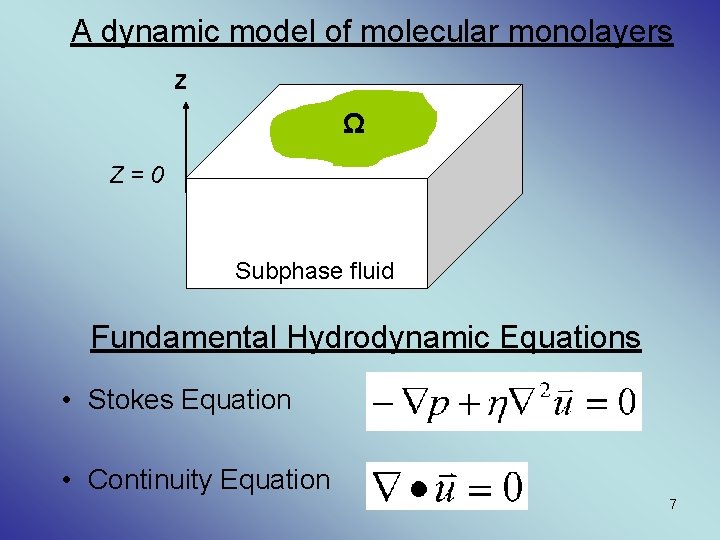
A dynamic model of molecular monolayers Z Ω Z=0 Subphase fluid Fundamental Hydrodynamic Equations • Stokes Equation • Continuity Equation 7

Assumptions on the subphase fluid • Horizontal flow • Boundary condition • Bulk viscosity ηbulk [Ref] Ref: Elizabeth K. Mann Hydrodynamics of Domain Relaxation in a Polymer Monolayer PRE 51 (6): 5708 -5720 JUN 1995 8

Assumptions on the surface • • 2 D Fluid (η and KG) One component [Ref 1]: – Elasticity KG [Ref 1]: Ω gas liquid – Surface pressure Π • • Surface Viscosities [Ref 2]: Electrostatic forces Ref 1: Ref 2: H. A. Stone; H. M. Mc. Connell; Proc. R. Soc. Lond. A 448: 97 -111 1995 9 Elizabeth K. Mann; PRE 51 (6): 5708 -5720 JUN 1995

Result on Small Distortion Limit For 2 D (n=2) L Ref: w H. A. Stone; H. M. Mc. Connell Hydrodynamics of quantized shape transitions of lipid domains Proc. R. Soc. Lond. A 448: 97 -111 1995 10

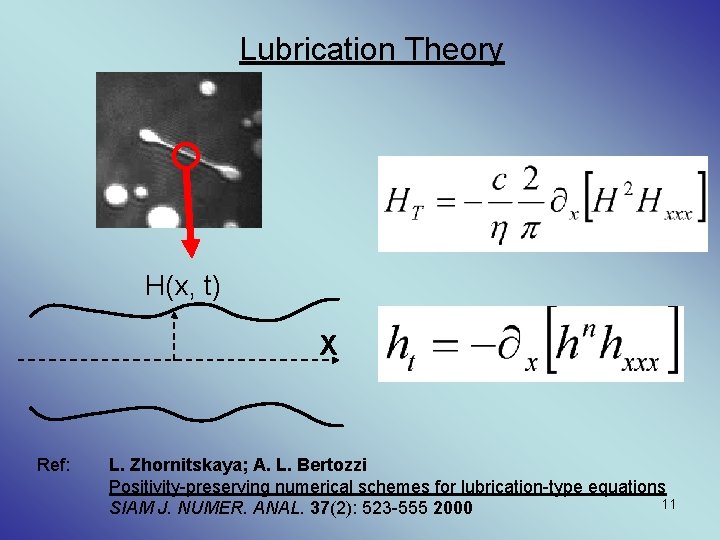
Lubrication Theory H(x, t) X Ref: L. Zhornitskaya; A. L. Bertozzi Positivity-preserving numerical schemes for lubrication-type equations 11 SIAM J. NUMER. ANAL. 37(2): 523 -555 2000

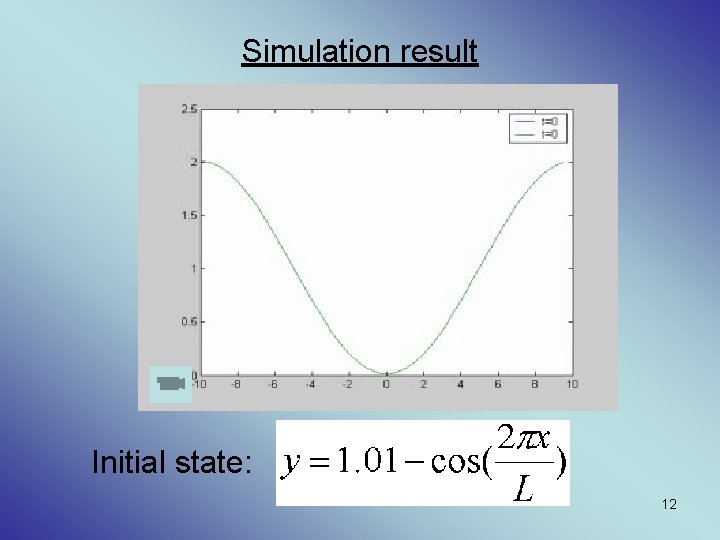
Simulation result Initial state: 12

Discussion on the Simulation • Periodic Boundary condition • No ends What constrains should be applied at the ends of the tether? 13

Hole Closing Poly(dimethyl)siloxane (PDMS) monolayer on water/air interface 14

Conclusion • A simplified model with assumptions close to the real experimental conditions Prospect • Line tension determination • Entire range of the relaxation behavior 15

Acknowledgement • Dr. Elizabeth K. Mann (Kent State University) • Dr. Andrew J. Bernoff (Harvey Mudd College) • Dr. James C. Alexander (Case Western Reserve University) • Dr. J. Adin Mann Jr. (Case Western Reserve University) • Ms. Violeta Beleva (Kent State University) • Ms. Ji Wang (Kent State University) • Supported by National Science Foundation under Grant No. 9984304 16

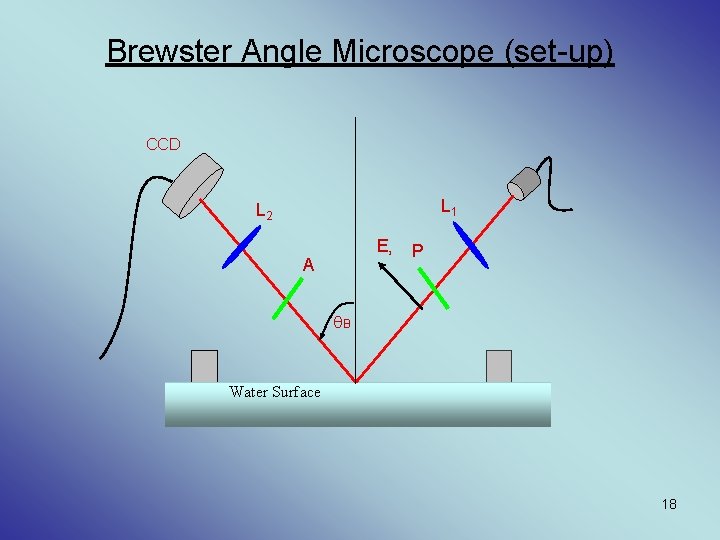
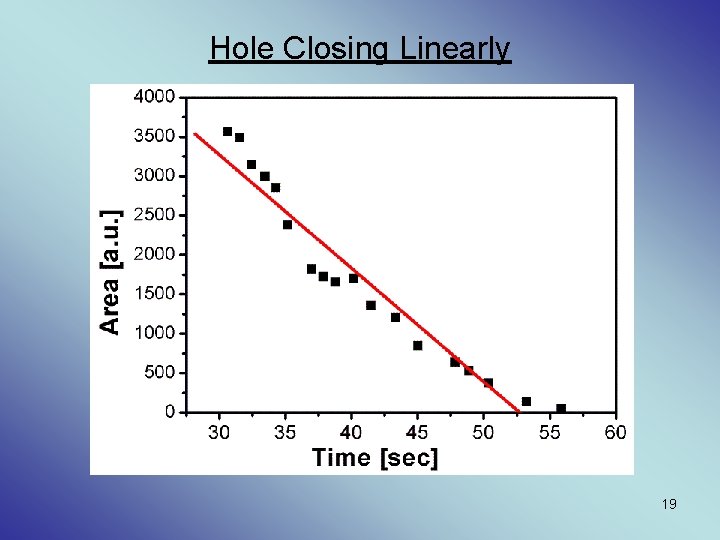
Frequent Questions • Brewster Angle Microscope (set-up) • Green Function Hele Shaw • F(n=2)=5 PI/16 (Stone); F(n=2)=5 PI/12 • Hole closing, linearly 17

Brewster Angle Microscope (set-up) CCD L 1 L 2 Ei A P B Water Surface 18

Hole Closing Linearly 19