458 Agestructured models continued Estimating from Leslie matrix

458 Age-structured models (continued): Estimating from Leslie matrix models Fish 458, Lecture 4

The facts on 458 • Finite rate of population increase • =er & r=ln( ), therefore Nt=N t • A dimensionless number (no units) • Associated with a particular time step (Ex: =1. 2/yr not the same as = 0. 1/mo) • >1: pop. ; <1 pop

458 Matrix Population Models: Definitions • Matrix- any rectangular array of symbols. When used to describe population change, they are called population projection matrices. • Scalar- a number; a 1 X 1 matrix • State variables- age or stage classes that define a matrix. • State vector- non-matrix representation of individuals in age/stage classes. • Projection interval- unit of time define by age/stage class width.

458 Basic Matrix Multiplication 4 x 1 + 3 x 2 + 2 x 3 = 0 2 x 1 - 2 x 2 + 5 x 3 = 6 x 1 - x 2 - 3 x 3 3 2 x 1 2 – 2 5 x 2 1 – 1 3 x 3 4 = 1 0 = 6 1

458 What does this remind you of? n(t + 1) = An(t) Where: A is the transition/projection matrix n(t) is the state vector n(t + 1) is the population at time t + 1 This is the basic equation of a matrix population model.

Eigenvectors & Eigenvalues 458 When matrix multiplication equals scalar multiplication v. A = v v, w = Eigenvector Aw = w = Eigenvalue • Rate of Population Growth ( ): Dominant Eigenvalue • Stable age distribution (w): Right Eigenvector • Reproductive values (v): Left Eigenvector Note: “Eigen” is German for “self”.

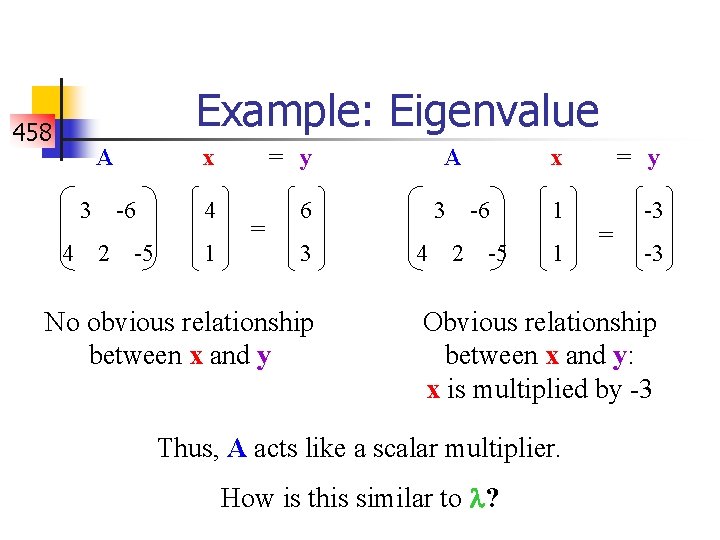
458 Example: Eigenvalue A x = y 3 -6 4 2 -5 1 3 = No obvious relationship between x and y A x = y 3 -6 1 -3 4 2 -5 1 = -3 Obvious relationship between x and y: x is multiplied by -3 Thus, A acts like a scalar multiplier. How is this similar to ?

Characteristic equations 458 From eigenvalues, we understand that Ax = x We want to solve for , so Ax - x = 0 (singularity) or (A- I)x = 0 “I” represents an identity matrix that converts into a matrix on the same order as A. Finding the determinant of (A- I) will allow one to solve for . The equation used to solve for is called the Characteristic Equation

458 Solution of the Projection Equation n(t+1) = An(t) 4 - P 1 F 2 2 - P 1 P 2 F 3 - P 1 P 2 P 3 F 4 = 0 or alternatively (divide by 4) 1 = P 1 F 2 -2 + P 1 P 2 F 3 -3 + P 1 P 2 P 3 F 4 -4 This equation is just the matrix form of Euler’s equation: 1 = Σ lxmxe-rx

458 Constructing an age-structured (Leslie) matrix model n n n Build a life table Birth-flow vs. birth pulse Pre-breeding vs. post-breeding census n n n Survivorship Fertility Build a transition matrix

458 n n Birth-Flow vs. Birth-Pulse Birth-Flow (e. g humans) Pattern of reproduction assuming continuous births. There must be approximations to l(x) and m(x); modeled as continuous, but entries in the projection matrix are discrete coefficients. Birth-Pulse (many mammals, birds, fish) Maternity function and age distribution are discontinuous, matrix projection matrix very appropriate.

Pre-breeding vs. Post-breeding Censuses 458 Pre-breeding (P 1) Populations are accounted for just before they breed. Post-breeding (P 0) Populations are accounted for just after they breed

Calculating Survivorship and Fertility Rates for Pre- and Post-Breeding Censuses 458 Different approaches, yet both ways produce a of 1. 221.

The Transition/Population Projection Matrix 458 4 age class life cycle graph

458 Example: Shortfin Mako (Isurus oxyrinchus) Software of choice: Pop. Tools

Mako Shark Data 458 Mortality: M 1 -6 = 0. 17 M 7 -w = 0. 15 Fecundity: 12. 5 pups/female Photo: Ron White Age at female maturity: 7 years Reproductive cycle: every other 2 years

Essential Characters of Population Models 458 Ø Asymptotic analysis: A model that describes the long-term behavior of a population. Ø Ergodicity: A model whose asymptotic analyses are independent of initial conditions. Ø Transient analysis: The short-term behavior of a population; useful in perturbation analysis. Ø Perturbation (Sensitivity) analysis: The extent to which the population is sensitive to changes in the model. Caswell 2001, pg. 18

458 Uncertainty and hypothesis testing Characterizing uncertainty • Series approximation (“delta method”) • Bootstrapping and Jackknifing • Monte Carlo methods Hypothesis testing • Loglinear analysis of transition matrices • Randomization/permutation tests Caswell 2001, Ch. 12

458 References Caswell, H. 2001. Matrix Population Models: Construction, Analysis, and Interpretation. Sunderland, MA, Sinauer Associates. 722 pp. Ebert, T. A. 1999. Plant and Animal Populations: Methods in Demography. San Diego, CA, Academic Press. 312 pp. Leslie, P. H. 1945. On the use of matrices in certain population mathematics. Biometrika 33: 183 -212. Mollet, H. F. and G. M. Cailliet. 2002. Comparative population demography of elasmobranch using life history tables, Leslie matrixes and stage-based models. Marine and Freshwater Research 53: 503 -516. Pop. Tools: http: //www. cse. csiro. au/poptools/