4 th year Electrical Engineering Department MAIN PRINCIPLES

4 th year – Electrical Engineering Department MAIN PRINCIPLES OF RADIATION Guillaume VILLEMAUD Antennas – G. Villemaud 0

First considerations Two important points: Most of antennas are metallic Huge majority of antennas are based on resonators In a metal, by default the free electrons move erratically. When creating a difference of potential (eg sinusoidal), the internal field then controls the distribution of charges. Currents and charges are then created as basic sources of electromagnetic field. But according to their distribution and relative phases, the overall field delivered by a metallic element is the sum of all contributions of these basic sources. Antennas – G. Villemaud 1

Radiation mechanism Charges transmitted over a straight metal at a constant speed do not produce radiation. +++ No radiation If the charges encountered a discontinuity (OC, bend. . . ) their speed changes, then there is radiation. +++ Radiation In a resonant structure, charges continuously oscillate, creating a continuous stream of radiation. High radiation +++ Antennas – G. Villemaud 2

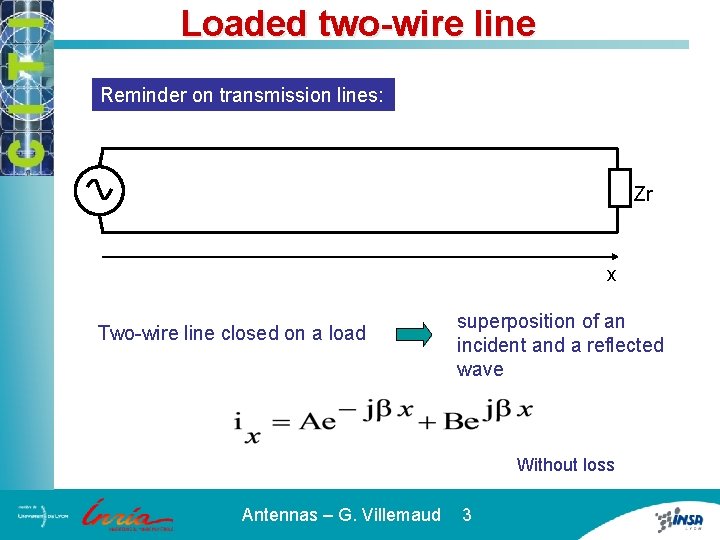
Loaded two-wire line Reminder on transmission lines: Zr x Two-wire line closed on a load superposition of an incident and a reflected wave Without loss Antennas – G. Villemaud 3

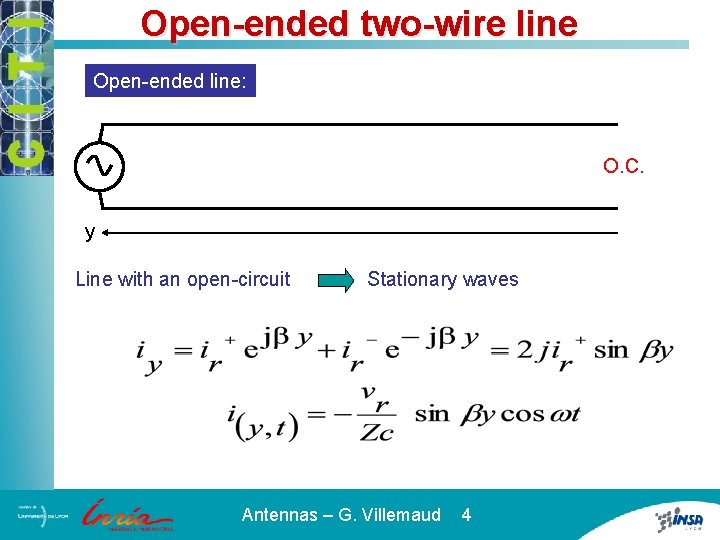
Open-ended two-wire line Open-ended line: O. C. y Line with an open-circuit Stationary waves Antennas – G. Villemaud 4

Resonant line C. O. Line with an open-circuit Stationary waves In practice, when the wires are relatively close, the currents are out of phase, the total radiated field is close to zero (thank goodness). Antennas – G. Villemaud 5

Bended wires The classical approximation considers that if the arms of the line are moved away, the current distribution remains the same. Antennas – G. Villemaud 6

Radiating dipole Then we have inphase currents for effective radiation: the principle of the dipole antenna Problem: in practice, there is mismatch. Then we seek a resonant antenna having an input impedance matched to a progressive wave line. Antennas – G. Villemaud 7

Reminder on EM fields Medium characteristics: To study phenomena of electromagnetic wave propagation, a medium will be defined by: Its complex electrical permittivity (F/m) Its complex electrical permeability Its conductivity (S/m) Antennas – G. Villemaud 8 electrical loss

Radiation sources Currents and charges present in this medium are called primary sources: Surface current density (A/m²) Volume charge density (Cb/m 3) These sources create: Electric and magnetic fields (V/m) (A/m) Other currents and charges and Induction phenomena Antennas – G. Villemaud 9

Maxwell’s Equations In an isotropic and homogeneous medium, we obtain these equations : Sources can be distributed as linear, surfacic or volumic densities. Antennas – G. Villemaud 10

Resolution domain Two distinct areas solving these equations are considered: in the presence of charges and currents or out of any charge or current. The resolution in the presence of charges and currents is used to determine the field distribution produced by a linear, surface or volume charges and currents (which leads to the radiation pattern of the antenna). The second type of resolution is required to calculate the electromagnetic waves propagated in free space (or in a particular medium). Antennas – G. Villemaud 11

Sinusoidal source Still in the case of homogeneous and isotropic media, with harmonic source the following equations are obtained: Then we can solve these equations to determine the field produced by the charges and currents present on a conductor. Antennas – G. Villemaud 12

Relation to the surface Interface with a perfect conductor 1, 1 The electric field is always perpendicular to the conductor. The magnetic field is always tangent to the conductor. The electric field is proportional to the charges on the surface. The magnetic field is proportional to the surface current. Antennas – G. Villemaud 13

EM potentials To assess the effects of an isotropic source at a point P of space we can introduce the vector and scalar potentials: Knowing that we can write z P q r o Vector A is defined in a gradient approximate, then there is a function V satisfying: y j x Antennas – G. Villemaud 14

EM potentials Expressing Maxwell's equations based on the potential, we obtain the wave equations: The resolution (based on the complex Green's functions) provides for a linear distribution: Scalar potential Vector potential Antennas – G. Villemaud 15

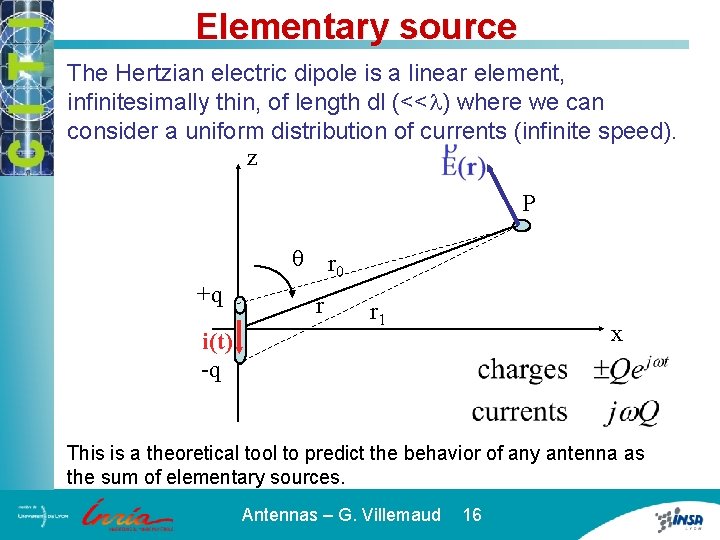
Elementary source The Hertzian electric dipole is a linear element, infinitesimally thin, of length dl (<<l) where we can consider a uniform distribution of currents (infinite speed). z P q r 0 +q i(t) -q r r 1 x This is a theoretical tool to predict the behavior of any antenna as the sum of elementary sources. Antennas – G. Villemaud 16

Radiated field calculation The problem is rotationally symmetrical relative to Oz. The vector potential has only one component Az: Then we obtain: The magnetic field has just one component: Antennas – G. Villemaud 17

Electric field calculation Then we can deduce the electric field which is produced : Electric field with two components: and So we end up finally with three components of the radiated field. Depending on the distance from the observation point P with respect to the source, we will do different approximations to simplify expressions. Antennas – G. Villemaud 18

Approximations depending on r The terms in 1/r represent the radiated field (predominant when large r) 1/r 2 terms give the induced fields and terms in 1/r 3 the electrostatic field. Antennas – G. Villemaud 19

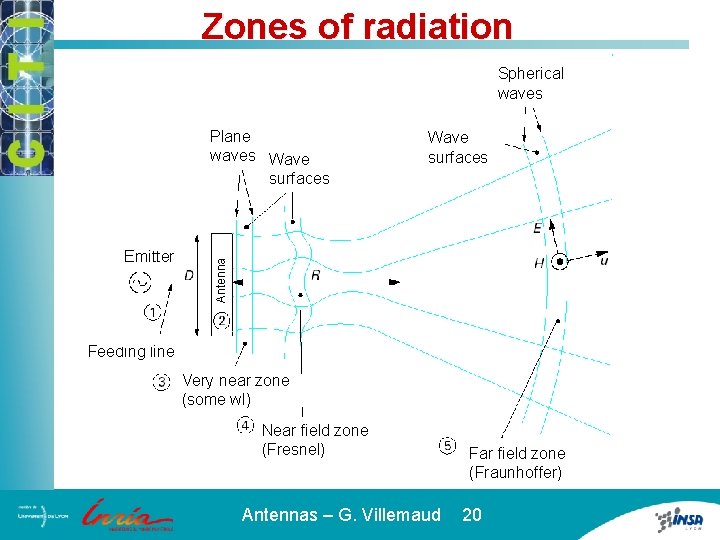
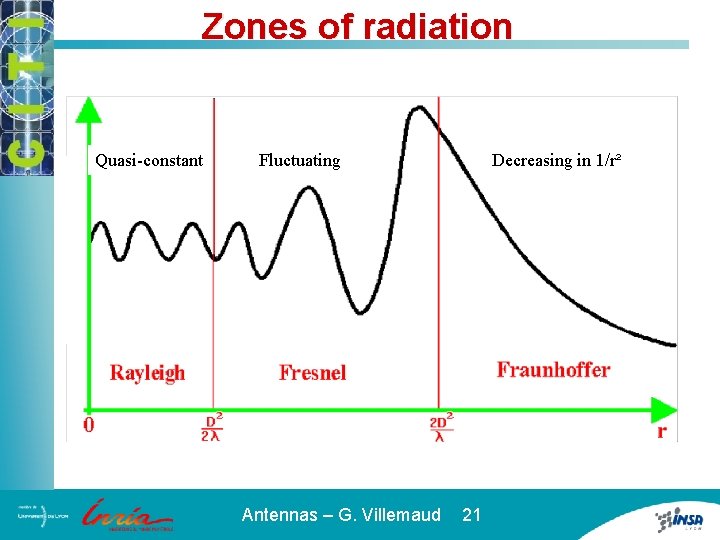
Zones of radiation Spherical waves Emitter Wave surfaces Antenna Plane waves Wave surfaces Feeding line Very near zone (some wl) Near field zone (Fresnel) Far field zone (Fraunhoffer) Antennas – G. Villemaud 20

Zones of radiation Quasi-constant Fluctuating Antennas – G. Villemaud 21 Decreasing in 1/r²

Hertzian dipole’s radiation Far field approximation : i(t) Free space Antennas – G. Villemaud 22

Farfield Propagation Returning to the harmonic equations in the case of homogeneous, isotropic media containing no primary sources, we obtain the following equations: Remark : In this case, we see that the equations in E and H are almost symmetrical, the only difference being the absence of charges and magnetic currents. We can then introduce fictitious magnetic sources for these symmetrical equations. The solution of the electrical problem then gives the magnetic problem solution and vice versa. Antennas – G. Villemaud 23

Propagation equations The propagation equations for the fields E and H (expressed in complex instantaneous values) are written as follows: If propagation is in the direction Oz, it comes: and The ratio represents the propagation speed of the wave. Antennas – G. Villemaud 24

Solutions In a sinusoidal steady state regime, these equations admit solutions of the form: and with : (wavenumber) The ratio between absolute values of and represents the wave impedance of the considered medium (in ohms): it’s a real value. In the air: 377 ohms We have a fundamental relation: Antennas – G. Villemaud 25

Spherical wave –Plane wave A point source (Q charge) produce radiation of a spherical wave. Indeed, solving the equations of potential in the case of a point source is symmetrical spherical revolution, and gives solution for: In Farfield, this leads to: The wave surface is a sphere centered at the point source Antennas – G. Villemaud 26

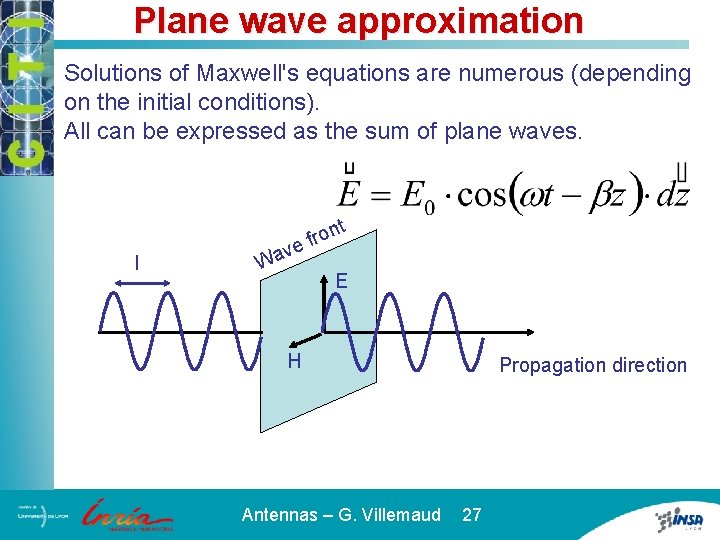
Plane wave approximation Solutions of Maxwell's equations are numerous (depending on the initial conditions). All can be expressed as the sum of plane waves. t l on r f ave W E H Antennas – G. Villemaud 27 Propagation direction

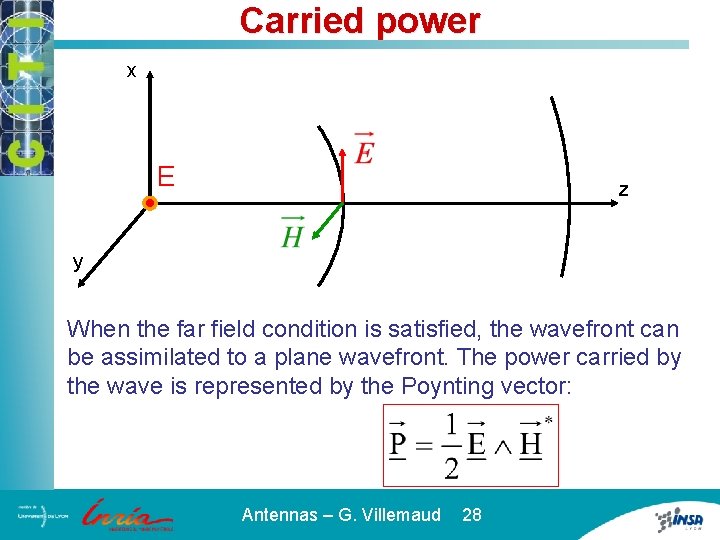
Carried power x E z y When the far field condition is satisfied, the wavefront can be assimilated to a plane wavefront. The power carried by the wave is represented by the Poynting vector: Antennas – G. Villemaud 28

Plane wave propagation Antennas – G. Villemaud 29

Polarization of the wave We know that far-field E and H are perpendicular to each other and perpendicular to the direction of propagation. But depending on the type of source used, the orientation of these vectors in the plane wave can vary. Based on the variations in the orientation of the field E over time, we define the polarization of the wave. In spherical coordinates, the components of the E field of a plane wave is described by: with and Antennas – G. Villemaud 30

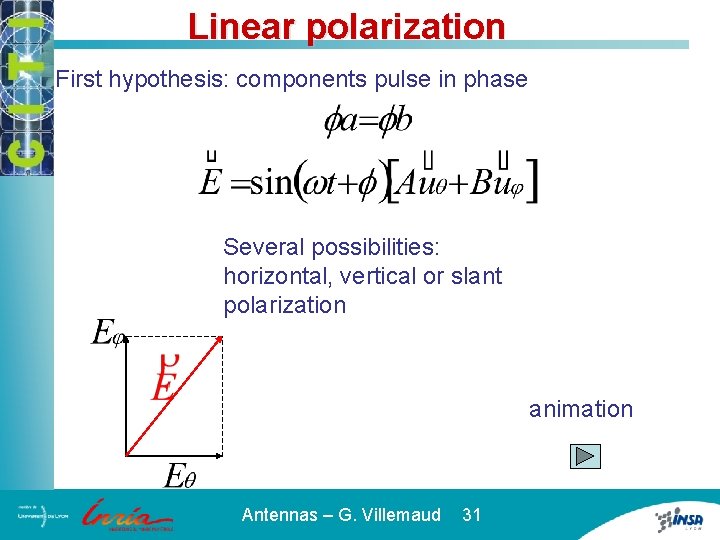
Linear polarization First hypothesis: components pulse in phase Several possibilities: horizontal, vertical or slant polarization animation Antennas – G. Villemaud 31

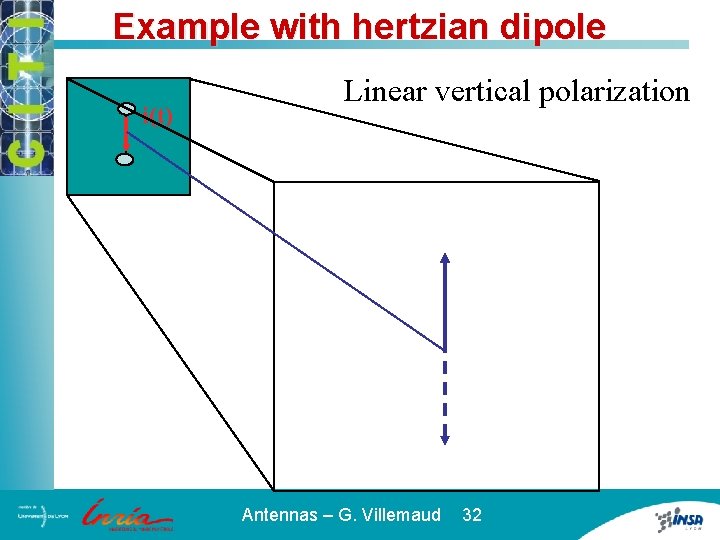
Example with hertzian dipole i(t) Linear vertical polarization Antennas – G. Villemaud 32

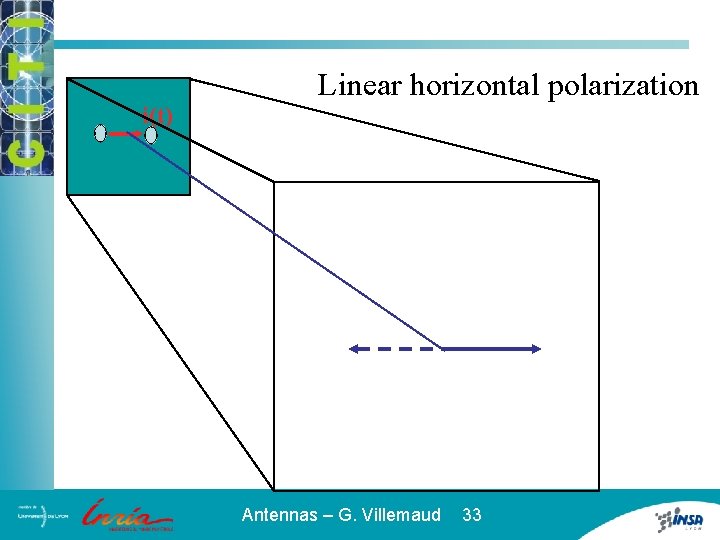
i(t) Linear horizontal polarization Antennas – G. Villemaud 33

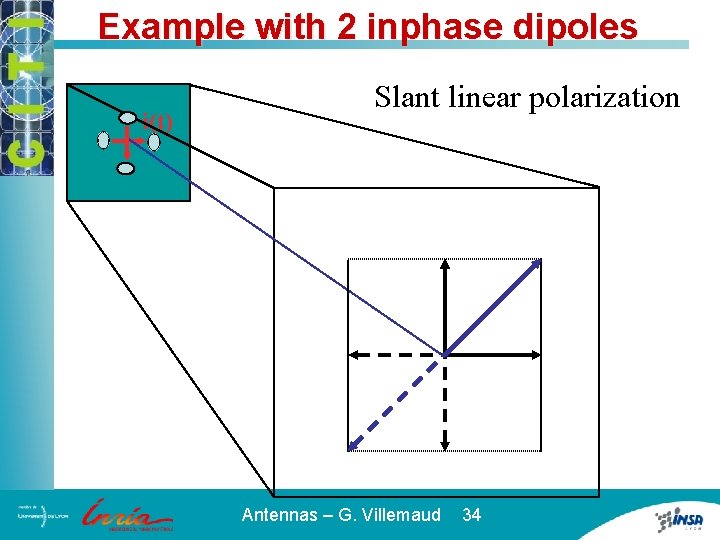
Example with 2 inphase dipoles i(t) Slant linear polarization Antennas – G. Villemaud 34

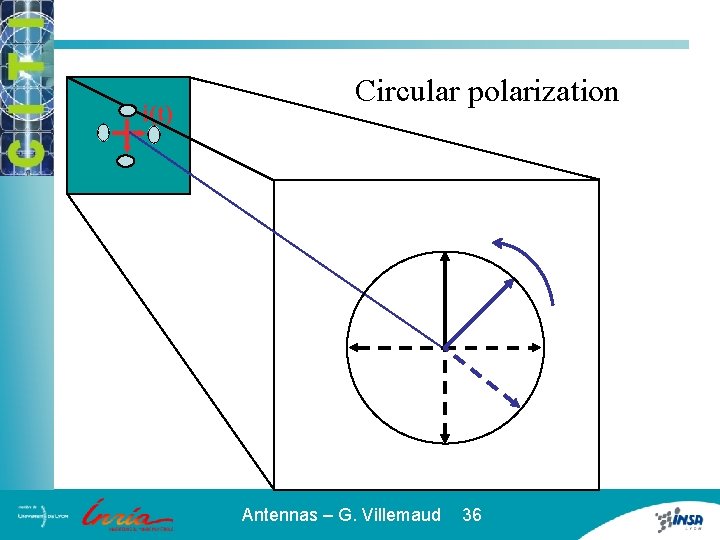
Circular polarization Second hypothesis: components vibrate in phase quadrature and magnitudes are equal Antennas – G. Villemaud 35

i(t) Circular polarization Antennas – G. Villemaud 36

Animations Antennas – G. Villemaud 37

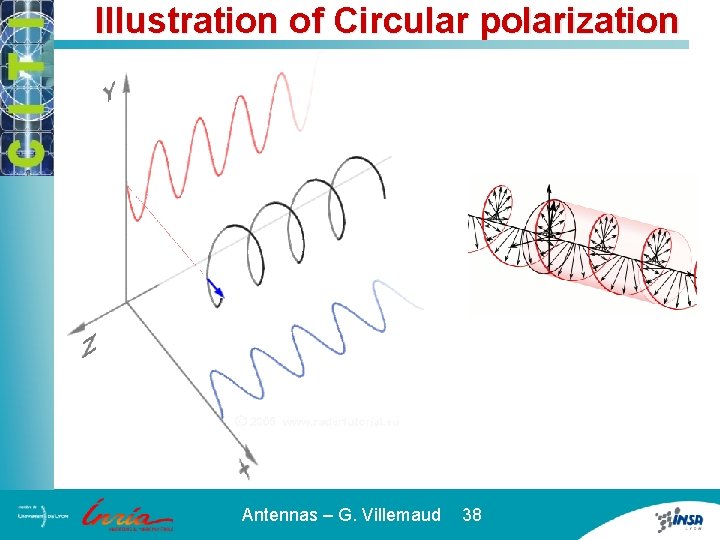
Illustration of Circular polarization Antennas – G. Villemaud 38

Elliptic Polarization 3 modes of polarization – Linear polarization • vertical, horizontal, slant (plane H or E) – Circular polarization • Left-hand or right-hand – Elliptic polarization • General definition Antennas – G. Villemaud 39

Fundamental theorems To study the functioning of antennas, four fundamental theorems are known: Ø Ø the Lorentz reciprocity theorem of Huygens-Fresnel the image theory Babinet's principle Antennas – G. Villemaud 40

Lorentz reciprocity If we consider that two distributions of currents I 1 and I 2 are the source of E 1 and E 2 fields, Maxwell's equations allow to write: radiating systems are reciprocal (note only in passive antennas). Pf Pr Pr Pf Antennas – G. Villemaud 41

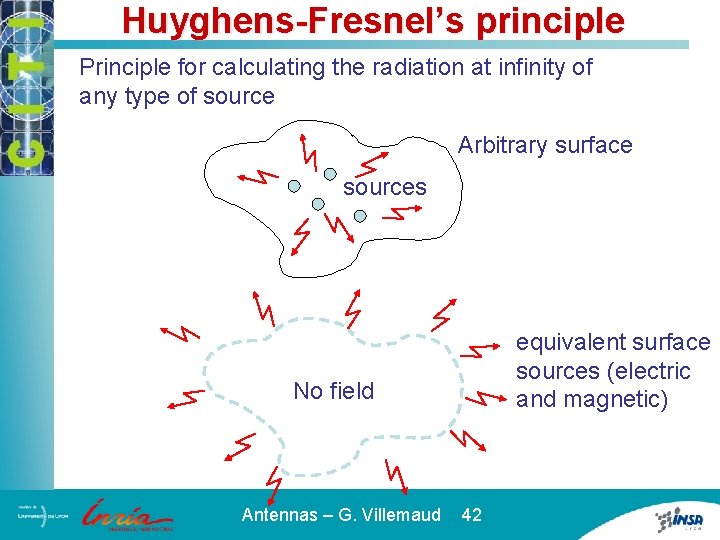
Huyghens-Fresnel’s principle Principle for calculating the radiation at infinity of any type of source Arbitrary surface sources No field Antennas – G. Villemaud 42 equivalent surface sources (electric and magnetic)

Application to radar Principle for bistatic radar Plane wave target P Observation point The field received in P is the sum of the field that would be received without the obstacle (known) and diffracted by the obstacle. It is then possible to calculate the inverse of the surface formed by sources providing such a field. Antennas – G. Villemaud 43

Image theory At an observation point P, the field created by a source + q placed above a perfect ground plane of infinite dimensions is equivalent to the field created by the combination of this charge with its image by symmetry with a charge -q. x +q P x +q -q Antennas – G. Villemaud 44 P

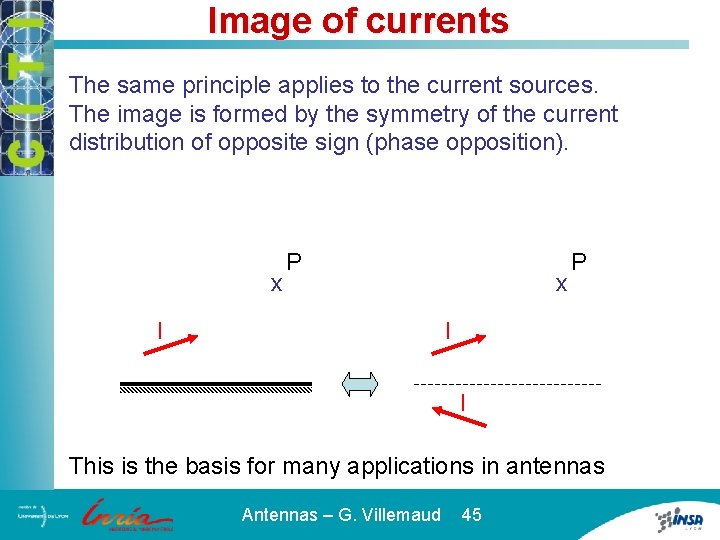
Image of currents The same principle applies to the current sources. The image is formed by the symmetry of the current distribution of opposite sign (phase opposition). x I P x P I I This is the basis for many applications in antennas Antennas – G. Villemaud 45

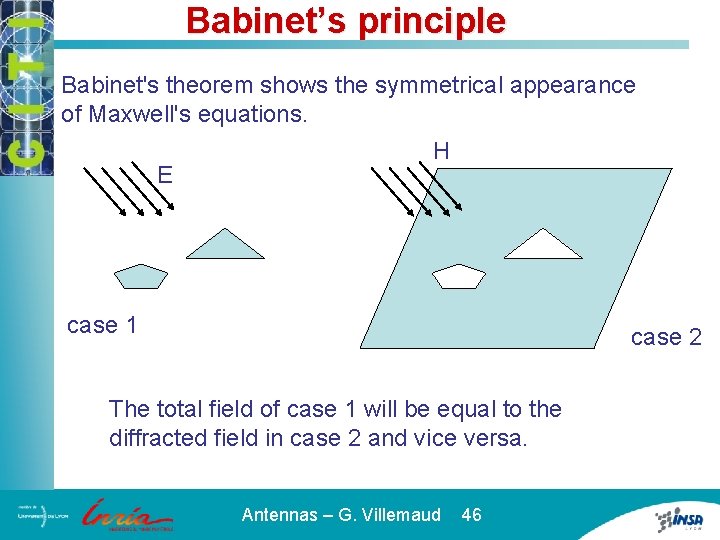
Babinet’s principle Babinet's theorem shows the symmetrical appearance of Maxwell's equations. E H case 1 case 2 The total field of case 1 will be equal to the diffracted field in case 2 and vice versa. Antennas – G. Villemaud 46

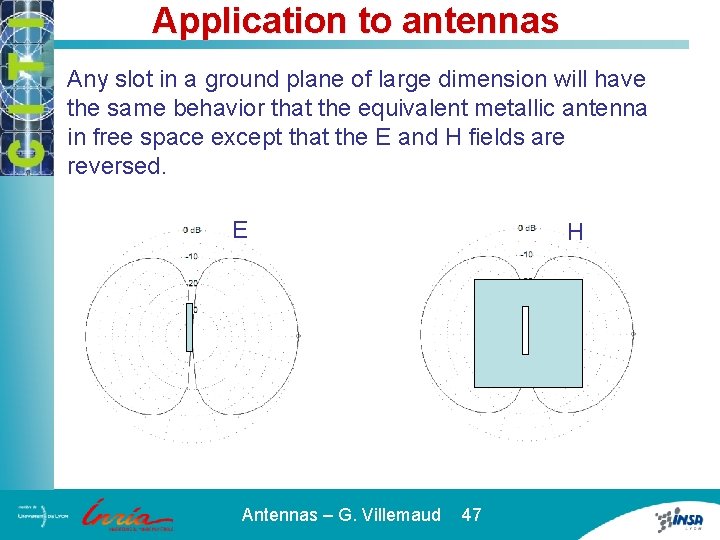
Application to antennas Any slot in a ground plane of large dimension will have the same behavior that the equivalent metallic antenna in free space except that the E and H fields are reversed. E Antennas – G. Villemaud 47 H