4 Predstavitev informacije in aritmetika po knjigi D

4 Predstavitev informacije in aritmetika po knjigi D. Kodek: Arhitektura in organizacija računalniških sistemov 1

Informacija • Informacija – Ukazi – Operandi • Števila – Fiksna vejica » Predznačena » Nepredznačena – Plavajoča vejica » Enojna natančnost » Dvojna natančnost • Nenumerični operandi – Logične spremenljivke – Znaki 2

Predstavitev nenumeričnih operandov • Pri prvih rač. so bili operandi samo numerični – danes je veliko nenumeričnih • Običajno so nenumerični operandi v obliki nizov (strings) znakov • Vsak znak (character) je predstavljen z neko abecedo – abeceda BCD • • do leta 1964 6 -bitna 26 črk, 10 številk, 28 posebnih znakov hitro je postala premajhna 3

– abeceda EBCDIC • • IBM, 1964 8 -bitna Extended Binary Coded Decimal Interchange Code razširitev abecede BCD 4

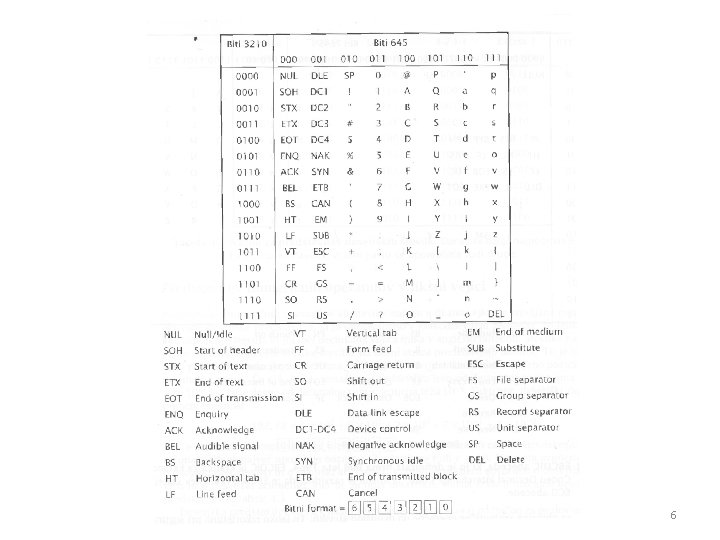
– abeceda ASCII • 1968 • ASCII - American Standard Code for Information Interchange • originalno 7 -bitna (128 znakov) – razširjena 8 -bitna • od tega 95 natisljivih (printable) znakov in 33 kontrolnih znakov (non-printable) – – A. . . 1000001 (65), B. . . 1000010 (66), . . . a. . . 1100001 (97), b. . . 1100010 (98), . . . 0110000 (48), 1. . . 0110001 (49), . . . !. . . 0100001 (33), “. . . 0100010 (34), . . . • kontrolni znaki za rač. komunikacije in krmiljenje V/I naprav 5

6

– Unicode • neprofitni konzorcij, 1991 • abecede UTF 8, UTF 16, UTF 32 7

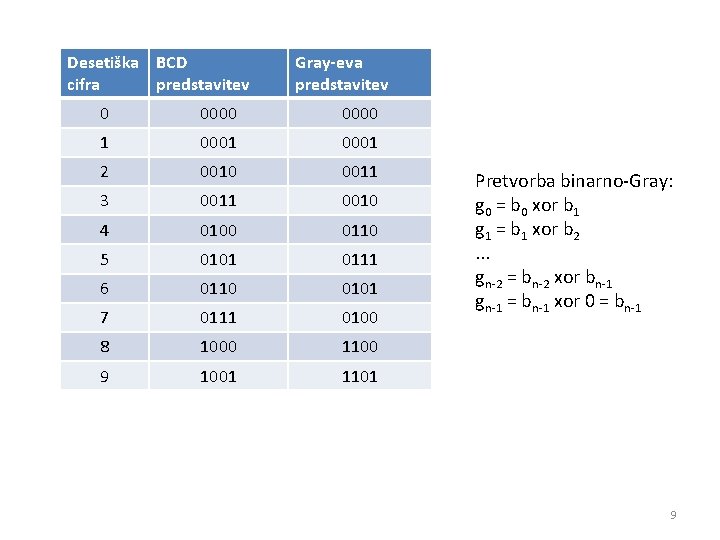
• Spodnji 4 biti znakov za desetiške cifre v ASCII in EBCDIC ustrezajo njihovi dvojiški numerični vrednosti – to je BCD (Binary Coded Decimal), binarna predstavitev desetiških cifer • to ni abeceda BCD! – Gray-eva koda ima to lastnost, da se dve sosedni številki razlikujeta le v enem bitu – 4 -bitna za števila do 15, ne le do 9 8

Desetiška BCD cifra predstavitev Gray-eva predstavitev 0 0000 1 0001 2 0010 0011 3 0011 0010 4 0100 0110 5 0101 0111 6 0110 0101 7 0111 0100 8 1000 1100 9 1001 1101 Pretvorba binarno-Gray: g 0 = b 0 xor b 1 g 1 = b 1 xor b 2. . . gn-2 = bn-2 xor bn-1 gn-1 = bn-1 xor 0 = bn-1 9

Predstavitev numeričnih operandov v fiksni vejici • Pozicijska notacija – vsaka cifra ima svojo težo • v skladu s pozicijo glede na vejico – 192, 73 = 1 102 + 9 101 + 2 100 + 7 10 -1 + 3 10 -2 – ta zapis lahko posplošimo na uteži oblike ri, kjer je r baza ali radix številskega sistema • npr. 215, 367 = 2 72 + 1 71 + 5 70 + 3 7 -1 + 6 7 -2 10

– v računalnikih se največ uporablja baza r=2, včasih pa tudi baza r=10 (poslovne aplikacije) • pri r=10 se za opis desetiških cifer običajno uporablja koda BCD (Binary Coded Decimal) 11

• Dvojiška (binarna) predstavitev (zapis) števil bn-1. . . b 2 b 1 b 0, b-1 b-2. . . b-m bi = 0 ali 1 vrednost 12

Pretvorba desetiških števil v bazo R • Algoritem: 1. 2. 3. • N : R = Q 1 + b 0 Ponavljaj 1. za Qi : R = Qi+1 + bi za vse i 1 Končaj, ko Qi = 0 Primer: pretvorba 9810 v bazo R=3 98 : 3 = 32 + 2 32 : 3 = 10 + 2 10 : 3 = 3 + 1 3: 3=1+0 1: 3=0+1 9810 = 101223 13

• Posebno nas zanima pretvorba v bazo R=2: 27 : 2 = 13 + 1 13 : 2 = 6 + 1 6: 2=3+0 3: 2=1+1 1: 2=0+1 2710 = 110112 14

Pretvorba ulomkov v bazo R • Algoritem: 1. Število N množimo z R, dobimo b-1 + F 1, 2. Ponavljaj 1. za Fi * R = b-(i+1) + Fi+1 za i=1, 2, . . . 3. Končaj, ko Fi = 0 • Primer: 0, 37510 v bazo R=2 0, 375 * 2 = 0, 750 * 2 = 1, 5 0, 5 * 2 = 1, 0 0, 37510 = 0, 0112 15

• N = 0. 510 v bazo 5: 0, 5 * 5 = 2, 5. . . 0, 510 = 0, 222. . . 5 16

• N = 0, 8 v bazo 3. Vzemimo toliko decimalk, da bo napaka manjša od 0, 01. 0, 8 * 3 = 2, 4 0, 4 * 3 = 1, 2 0, 2 * 3 = 0, 6 * 3 = 1, 8 0, 8 * 3 = 2, 4. . . 0, 810 = 0, 2101. . . R-k < 0, 01 17

|N - N’| < 0, 01 3 -k < 0, 01 log 33 -k < log 30, 01 logac = logab * logbc (na ta način se znebimo baze b, v našem primeru b=3) loge 0, 01 = loge 3 * log 30, 01 = ln 0, 01 / ln 3 = -4, 19 -k < -4, 19 k > 4, 19 k = 4, 19 k = 5 (3 -5 = 1/243, 3 -4 = 1/81) 0, 810 = 0, 21012 18

Primeri • N = 751, 310 v bazo R=7. |N-N’| < 0, 023 2122, 27 • N = 751, 310 v bazo R=11. |N-N’| < 10 -3 623, 33311 19

• Pretvorba R’ v R: 1. R’ v 10 2. 10 v R • 26, 58 v R=3 211, 1212. . . 3 20

• Poleg dvojiške se v računalništvu pogosto uporabljata tudi osmiška (oktalna) in še posebno šestnajstiška (heksadecimalna) baza – ker sta ti bazi sorodni bazi 2, je pretvorba enostavna – pri osmiški bazi ena cifra predstavlja 3 bite (dvojiške baze), pri šestnajstiški pa 4 bite – npr. 11100101012 = 1 110 010 1012 = 16258, 3278 = 011 010 1112 – npr. 11100101012 = 11 1001 01012 = 39516 oz. 395 H A 1516 = 1010 0001 01012 – v 16 -iški bazi so poleg 0. . 9 še dodatne cifre: • A (10), B (11), C (12), D (13), E (14), F (15) – 16 -iška baza se pogosto uporablja za krajši zapis binarnih števil 21

Primeri • • 1 A 11 = 1(10)11 v R=2, 11011 v R=7, Reši enačbo 40 y = 446 Reši enačbo x 1 y = 111 x 10101 2467 22

• Z n biti lahko zapišemo nepredznačena števila od 0 do 2 n-1 (z n biti lahko v kateremkoli formatu zapišemo 2 n števil) – npr. pri n = 3, števila od 0 (000) do 7 (111) – npr. pri n = 10, števila od 0 (000. . . ) do 1023 (111. . . ) 23

Seštevanje, odštevanje in množenje nepredznačenih števil • • • 23459 + 162509 = 186059 212023 + 120123 = 1102213 41025 – 24305 = 11225 33067 – 6157 = 23617 3245 * 235 = 141125 11012 * 1012 = 10000012 24

Predstavitev predznačenih števil bn-1. . . b 2 b 1 b 0 • Predznak in velikost – prvi bit (bn-1) predstavlja predznak, ostali velikost – slabo je, da je treba predznak obravnavati posebej – ni primerna za seštevanje/odštevanje • poleg tega ima -0 in +0 – primerna za množenje/deljenje • manj pogosti operaciji 25

• Predstavitev z odmikom – odmik je -2 n-1 – nekoč popularna – hiba: • pri seštevanju je treba odmik prišteti – abs. vrednost odšteti • pri seštevanju je treba odmik odšteti – abs. vrednost prišteti 26

010 (-2) +101 (1) ----111 (3) -100 ---011 (-1) 101 +101 ---1010 -0100 ----110 (2) 2 -4 5 -4 --7 -4 -4 010 +011 ---101 -100 ---001 110 (2) 6 -4 -101 (1) 5 -4 ---001 1 +100 ---101 1+4 -4 (-2) (-1) (-3) 27

• Eniški komplement (1’K) – tudi tu je bn-1 predznak – pozitivna števila (bn-1=0) enako kot pri predstavitvi PV – negativno število dobimo iz pozitivnega z invertiranjem vseh bitov • ekvivalentno odštevanju od 2 n – 1 (same enice) – predznaka ni treba obravnavati posebej (drugače od ostalih bitov)! – hibe: • 2 ničli (-0, +0) • pri prenosu z najvišjega mesta je treba na najnižjem mestu prišteti 1 (End Around Carry - EAC) 28

Npr. , n=3: 010 +110 ---1000 001 101 (-2) +110 (-1) ---1011 -111 ---100 a-c=a+(-c)=a+2 n-1 -c=010+111 -001 111=1000 -1 -111=-1000+1 1011 -1000 + 1 ----100 (-3) 29

n=4: 0110 (6) +1100 (-3) ----10010 -10000 + 1 ----0011 (3) 30

• Dvojiški komplement (2’K) – podoben eniškemu, le da negativno število dobimo tako, da invertiramo vse bite pozitivnega števila (eniški komplement) in prištejemo 1 • ekvivalentno odštevanju od 2 n • npr. 0010 (2) 1101 (-2 v 1’K) + 1 1110 (-2 v 2’K) 31

– predznaka ni treba obravnavati posebej (drugače od ostalih bitov)! – 2’K je najpogosteje uporabljan zapis • primeren za seštevanje/odštevanje (poleg tega nima EAC) • le ena predstavitev za ničlo 32

a-c=a+(-c)=a+2 n-c=a-c+2 n 011 +110 ---1001 33

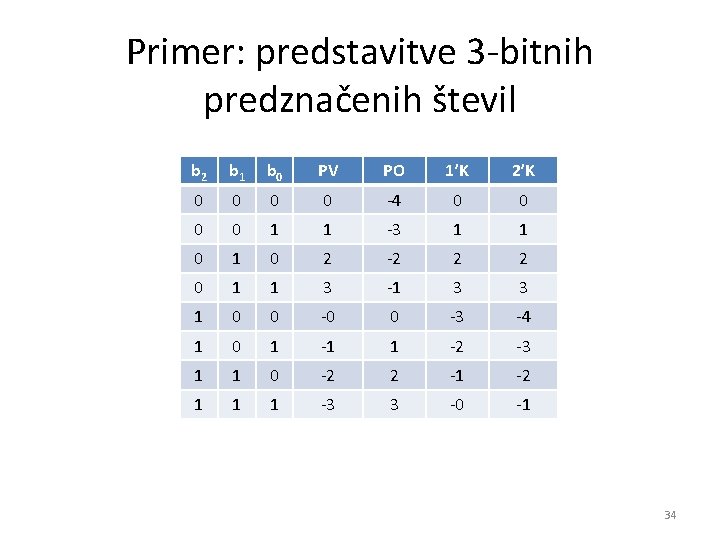
Primer: predstavitve 3 -bitnih predznačenih števil b 2 b 1 b 0 PV PO 1’K 2’K 0 0 -4 0 0 1 1 -3 1 1 0 2 -2 2 2 0 1 1 3 -1 3 3 1 0 0 -3 -4 1 0 1 -1 1 -2 -3 1 1 0 -2 2 -1 -2 1 1 1 -3 3 -0 -1 34

• Obseg števil v n-bitnem 2’K: -2 n-1 x 2 n-1 – 1 npr. pri n=3: -4 x 3 • Če je (pravi) rezultat operacije izven tega območja, je prišlo do preliva (overflow) – rezultat je napačno število – preliv se da detektirati • Preliv ni isto kot prenos (carry) z najvišjega mesta – le-ta se nanaša na operacije z nepredznačenimi števili, kjer je območje 0 x 2 n – 1 – pri dvojiškem komplementu se prenos ignorira! 35

• Kdaj pride do preliva? – potreben pogoj je, da imata števili (ki ju seštevamo) enak predznak – zadosten pogoj pa je, da ima vsota drugačen predznak kot števili • Pogoj za preliv (OF) bi lahko zapisali kot OF = xn-1 yn-1 sn-1’ xn-1’yn-1’sn-1 (a’ pomeni negacijo a) vendar je možno tudi enostavneje (kot bomo videli) 36

• Primeri operacij v 4 -bitnem 2’K: 0100 (4) 0101 (5) 1100 (-4) + 0011 (3) +0100 (4) +0101 (5) 0111 (7) 1000 (-8) 1 0001 (1) 1010 (-6) +1011 (-5) 1 0101 (5) • Če želimo število v 2’K razširiti na več bitov, razširimo predznak: – npr. 0011 v 000011 – npr. 1010 v 111010 37

Primeri • Zapiši -37 kot predznačeno 10 -bitno število v PV, 1’K in 2’K • Seštej (-21)+(-7) v 6 -bitnem 2’K 38

Aritmetika v fiksni vejici • 1 -bitni seštevalnik – polovični (Half Adder, HA) • sešteva 2 bita, izračuna vsoto (s, sum) in (izhodni) prenos (c, carry) s = x y (= xy’ + x’y) c = xy (= x&y) – polni (Full Adder, FA) • sešteva 3 bite, izračuna vsoto in (izhodni) prenos s = x y z (= x’y’z + x’yz’ + xy’z’ + xyz) c = xy + xz + yz 39

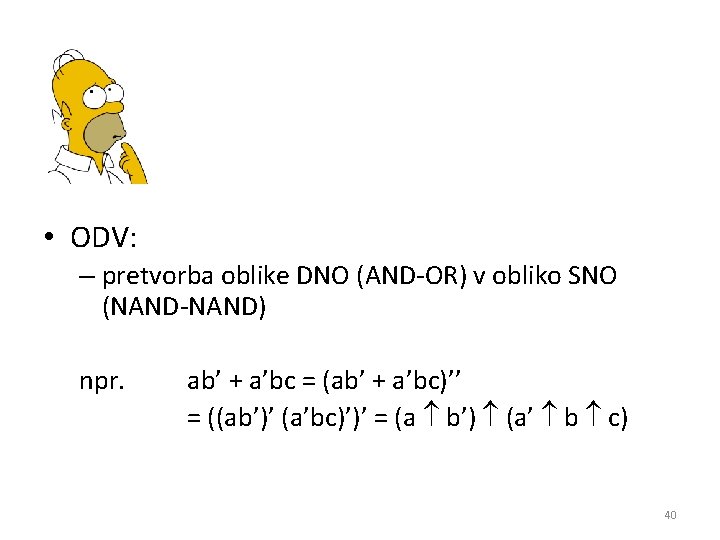
• ODV: – pretvorba oblike DNO (AND-OR) v obliko SNO (NAND-NAND) npr. ab’ + a’bc = (ab’ + a’bc)’’ = ((ab’)’ (a’bc)’)’ = (a b’) (a’ b c) 40

• Dejanska realizacija uporablja NAND (ali NOR) s = x’y’z + x’yz’ + xy’z’ + xyz = (x’ y’ z) (x’ y z’) (x y’ z’) (x y z) 3 nivoji vrat zakasnitev: 3 ( . . . zakasnitev enih vrat) c = xy + xz + yz = (x y) (x z) (y z) 2 nivoja vrat zakasnitev: 2 41

• Večbitni seštevalnik – Seštevalnik z razširjanjem prenosa (Ripple Carry Adder, RCA) • zaporedna vezava 1 -bitnih FA • izhodni prenos nižjega vezan na enega od vhodov višjega – običajno se en vhod imenuje kar vhodni prenos (cin) s = x y cin cout = xy + xcin + ycin • hiba: zakasnitev – v najslabšem primeru se prenos razširja čez vse FA 42

Dejanska zakasnitev je odvisna od operandov: – Npr. 0101+1100 c 1: 2 , c 2: 2 , c 3: 2 , c 4: 4 s 0: 3 , s 1: 5 , s 2: 5 , s 3: 5 – Npr. 1011+0101 ali 1111+0001, (najslabši primer) c 1: 2 , c 2: 4 , c 3: 6 , c 4: 8 s 0: 3 , s 1: 5 , s 2: 7 , s 3: 9 cn-1, max = 2 n , sn-1, max = (n-1)2 + 3 = 2 n + 1 Maksimalna zakasnitev praktično linearno narašča 43

– Seštevalnik z vnaprejšnjim prenosom (Carry. Lookahead Adder, CLA) • hiter izračun vseh prenosov – le na osnovi vhodov x, y in c 0 • dodatna logika Generiranje prenosa v i-ti stopnji g i = xiy i generate Razširjanje prenosa preko i-te stopnje p i = xi + y i propagate (namesto pi = xi yi) 44

Mimogrede: – sprememba večnivojske oblike v dvonivojsko: npr. ab’ + a’(bc’ + d) = ab’ + a’bc’ + a’d 45

ci+1 = gi + pici c 1 = g 0 + p 0 c 0 c 2 = g 1 + p 1 c 1 (!) = g 1 + p 1(g 0 + p 0 c 0) = g 1 + g 0 p 1 + c 0 p 1 c 3 = g 2 + p 2 c 2 (!) = g 2 + p 2(g 1 + g 0 p 1 + c 0 p 0 p 1) = g 2 + g 1 p 2 + g 0 p 1 p 2 + c 0 p 1 p 2 c 4 =. . . = g 3 + g 2 p 3 + g 1 p 2 p 3 + g 0 p 1 p 2 p 3 + c 0 p 0 p 1 p 2 p 3. . . 46

• vsi prenosi so dvonivojske funkcije g, p in c 0 • g = xiyi = (xi yi)’ – 1 nivo, pri NAND 2 nivoja • p = xi + yi = (xi’ yi’) de. Morgan – 1 nivo, pri NAND 2 nivoja • Skupno 4 nivoji: zakasnitev prenosov 4 • 4 + 3 = 7 – fiksna zakasnitev! – npr. n=16: • RCA: 33 • CLA: 7 – nad n=16 se CLA ne uporablja direktno • več manjših 47

• Seštevanje in odštevanje predznačenih števil v 2’K (z enim vezjem) – signal M (Add’/Sub) določa operacijo • 0: + • 1: - – odštevanje • • • X – Y = X + Y’ + 1 -Y kot dvojiški komplement Y Y’ = (yn-1’. . . y 1’ y 0’) yi M XOR dela kot krmiljen negator yi 0 = yi y i 1 = y i’ • +1: M vežemo na c 0 48

• Detekcija preliva – enak predznak operandov – drugačen predznak vsote OF = xn-1 yn-1 sn-1’ xn-1’yn-1’sn-1 – pri prvem produktu je cn-1=0 in cn=0, pri drugem obratno, zato OF = cn-1 cn 49

• Binarno množenje – tvorba delnih (parcialnih) produktov (n*n konjunkcij) – seštevanje delnih produktov x 2 x 1 x 0 * y 2 y 1 y 0 ----------------x 2 y 2 x 1 y 2 x 0 y 2 x 2 y 1 x 1 y 1 x 0 y 1 x 2 y 0 x 1 y 0 x 0 y 0 ----------------- 50

• Delni produkt je enak množencu, če je ustrezni bit množitelja enak 1, sicer je enak 0 – 2 vrsti metod: • pomikanje in seštevanje – 1 bit / cikel ure – poceni, a ne prav hitro – registri • kombinacijski množilniki – brez ure – dragi, a hitri 51

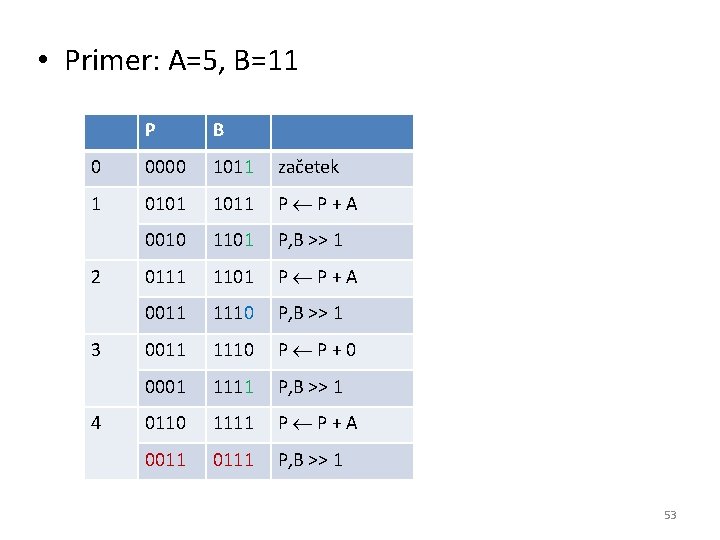
• Množenje s pomiki in seštevanjem – Postopek iz n korakov: • Če je najnižji bit množitelja B enak 1, prištej množenec A registru P (na začetku 0) – sicer prištej 0 • Pomik desno registrov P in B (kaskadno vezanih) 52

• Primer: A=5, B=11 P B 0 0000 1011 začetek 1 0101 1011 P P+A 0010 1101 P, B >> 1 0111 1101 P P+A 0011 1110 P, B >> 1 0011 1110 P P+0 0001 1111 P, B >> 1 0110 1111 P P+A 0011 0111 P, B >> 1 2 3 4 53

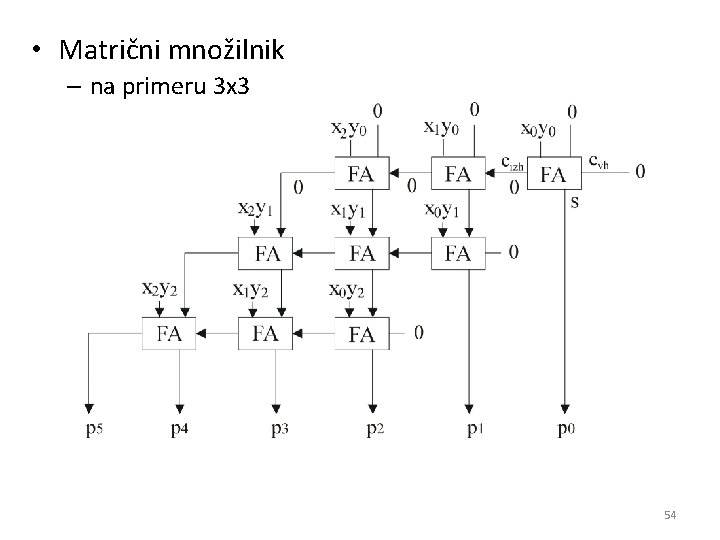
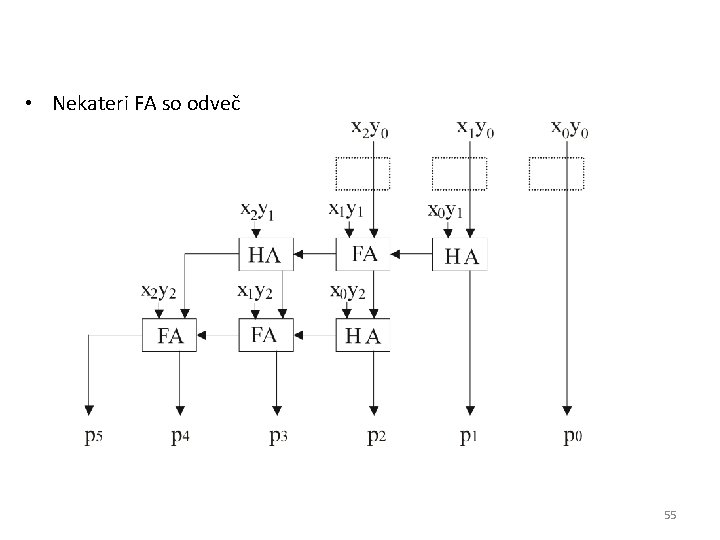
• Matrični množilnik – na primeru 3 x 3 54

• Nekateri FA so odveč 55

– Zakasnitev linearna • (3 n-2) FA • (3 n-4) FA – Obstajajo tudi metode za hitro seštevanje več sumandov, t. i. paralelni števniki (parallel counters) • Wallace, Dadda, . . . • glavna aplikacija je množenje 56

• Množenje v 2’K – Booth-ov algoritem • Binarno deljenje – 2 osnovna načina: • zaporedje odštevanj in pomikov • matrični delilnik – enobitni odštevalniki 57

• Problemi pri vključitvi aritmetike v rač. sistem: 1. Preliv • 2 rešitvi: – – postavitev posebnega bita sprožitev pasti (nek bit lahko določa, ali se sproži, ali pa se ignorira) 2. Dolžina produkta • produkt dveh števil je shranjen v spremenljivki enake velikosti kot števili – produkt dveh n-bitnih števil je sicer 2 n-biten 3. Izvajanje operacij v eni urini periodi • • množenje in deljenje sta zahtevnejši operaciji 2 rešitvi: a) b) ukazi korak-množenja množenje izvaja posebna enota » lahko FPU (floating point unit) » CPU čaka na izračun 58

Predstavitev števil v plavajoči vejici • Obseg števil v fiksni vejici je za določene probleme premajhen – zelo velika ali zelo majhna števila • Znanstvena notacija omogoča krajši zapis – npr. 1 1018 namesto 1 000 000 000 • Število lahko zapišemo kot m re – m je mantisa, r je baza (običajno 2), e je eksponent – s spreminjanjem eksponenta vejica plava vzdolž mantise levo in desno (odtod ime plavajoča vejica) 59

• V plavajoči vejici lahko zapišemo bistveno večja, pa tudi bistveno manjša števila kot v fiksni – kljub temu pa je možnih števil enako mnogo (2 n) • Vsako število lahko v plavajoči vejici zapišemo na več načinov: – npr. 1 1018 = 10 1017 = 0, 1 1019. . – npr. 1 23 = 10 22 = 0, 1 24. . . – zato mantiso normiramo: • prvi bit je 1 (normalni bit), implicitno predstavljen 60

• Npr. : mantisa 01001. . . pomeni 1, 01001. . . – zelo majhnih števil ni mogoče predstaviti v normirani obliki • denormirana števila • podliv (underflow) • Eksponent je predstavljen v predstavitvi z odmikom • Vsak proizvajalec je uporabljal svoj format zapisa v plavajoči vejici – isti program je lahko na različnih računalnikih dajal različne rezultate 61

• Standard IEEE 754 (1985) – enojna natančnost (single precision), 32 bitov • 8 -biten eksponent e z odmikom 127 (e = E - 127) • 23 -bitna mantisa m (7 -mestna desetiška natančnost) • normirana vrednost je (-1)S(1, m)2 E-127, E = 1, 2, . . . , 254 – dvojna natančnost (double precision), 64 bitov • 11 -biten eksponent e z odmikom 1023 (e = E - 1023) • 52 -bitna mantisa m (16 -mestna desetiška natančnost) • normirana vrednost je (-1)S(1, m)2 E-1023, E = 1, 2, . . . , 2046 IEEE: Institute of Electrical and Electronics Engineers 62

63

• Primer: število 2 2 = +1. 0*21 m=0 32: e = 1, E = e + 127 = 128 = 10000000 64: e = 1, E = e + 1023 = 1024 = 100000 31 30 0 0 1000000000000 63 62 0 23 22 52 100000 51 0 0000000000000. . . 00000 64

• Primer: število -8. 25 = -1000. 01 = -1. 00001*23 m = 0000100. . . 32: e = 3, E = e + 127 = 130 = 10000010 64: e = 3, E = e + 1023 = 1026 = 1000010 31 30 1 0 1000001000000000 63 62 1 23 22 52 1000010 51 0 000010000000000. . . 00000 65

• Dovoljena so tudi denormirana števila (zelo majhna števila) – E=0 – implicitni normalni bit je enak 0 – vrednost v 32 -bitnem formatu je (-1)S(0, m)2 -126 • eksponent je -126 namesto -127, ker imamo (0, m) namesto (1, m) – vrednost v 64 -bitnem formatu je (-1)S(0, m)2 -1022, • eksponent je -1022 namesto -1023, ker imamo (0, m) namesto (1, m) – tudi 0 je denormirano število, ki ima mantiso enako 0 66

• Še dve posebni vrsti števil: – neskončnosti • E = 255 (v 32 -bitnem formatu) oz. E = 2047 (v 64 bitnem formatu), vsi biti E so 1 • če m=0, imamo + in - • pojavijo se, kadar je rezultat prevelik (npr. 1/0 da + ) – Na. N • ravno tako E = 255 oz. 2047 • m 0 • pojavijo se kot rezultat nedefiniranih operacij – npr. 0 , 0/0, - , kvadratni koren negativnega števila, . . . • rezultat operacije, ki vsebuje operand Na. N, je tudi Na. N 67

Aritmetika v plavajoči vejici • Aritmetika v plavajoči vejici se obravnava in realizira ločeno od aritmetike v fiksni vejici – bolj zapletena • Zaokroževanje – kadar je vrednost, ki jo je treba zaokrožiti, enako oddaljena od dveh najbližjih števil, se po standardu IEEE 754 zaokroži k sodemu številu – pri računanju mantiso podaljšamo za 3 dodatne bite • varovalni bit (guard bit) • zaokroževalni bit (round bit) • lepljivi bit (sticky bit) 68

• Varovalni bit je potreben, ker je vsota lahko za eno mesto daljša od operandov • Zaokroževalni bit je potreben, da lahko pravilno zaokrožimo • Primer: desetiška predstavitev z mantiso dolžine 3 – dodamo varovalno in zaokroževalno mesto (tretjega zaenkrat pustimo) • tako je mantisa 5 -mestna – pri seštevanju/odštevanju po pravilu število z manjšim eksponentom zapišemo z večjim eksponentom (mantisa se zato pomakne desno) 1, 01*104 – 3, 76*102 = (1, 0100 – 0, 0376)*104 = 0, 9724*104 = zaokr. 9, 72*103 – če bi uporabili le 4 -mestno mantiso, bi dobili napačno 9, 73*103 69

• Lepljivi bit se uporablja zaradi zaokroževanja k sodemu številu • Primer: (brez lepljivega bita) 4, 56*100 + 5, 01*10 -3 = (4, 5600 + 0, 0050)*100 = 4, 5650*100 = zaokr. 4, 56*100 – natančna vrednost bi bila 4, 56501 (zato bi bil bolj pravilen rezultat 4, 57), vendar zaradi pomika mantise v desno zadnja enica izpade – lepljivi bit pove, ali je desno od zaokroževalnega mesta še kako od nič različno mesto • v tem primeru je treba zaokrožiti navzgor (ne navzdol zaradi morebitnega najbližjega sodega števila) 70 • izračuna se kot funkcija ALI izpadlih bitov

• Seštevanje (in odštevanje) v plavajoči vejici 1. prvo število naj bo tisto z večjim eksponentom (začasni eksponent) 2. pomik mantise drugega števila 3. seštevanje (odštevanje) mantis 4. Če preliv, zmanjšaj mantiso (pomik) in povečaj začasni eksponent 5. Zaokrožitev mantise, bita r in s. . . 71

• Primer: 20, 75 + 0, 2500011 v enojni natančnosti 20, 75 = 10100, 11, normiramo: A = 1, 01001 100000 000*24 0, 2500011 = 0, 01000 000001 00101 , normiramo: B = 1, 00000 00100 101*2 -2 mantiso B pomaknemo za 6 mest: B = 0, 00000 100000 000|100101*24 B = 0, 00000 100000 000|101*24 A: 1, 01001 100000 000|000*24 B: + 0, 00000 100000 00000 000|101*24 S: 1, 01010 00000 001*24 (zaokroženo) – če ne bi upoštevali lepljivega bita, bi. . . 000|10 zaokrožili navzdol na. . . 000, z upoštevanjem lepljivega bita pa. . . 000|101 zaokrožimo navzgor na. . . 001 72

• Množenje v plavajoči vejici – eksponenta seštejemo, mantisi zmnožimo z množilnikom (fixed-point) • Primer: A*B A = 1, 01*22, B = 1, 11*20, začasni eksponent = 2 + 0 = 2 1, 01*1, 11 101 10, 0011 *22, normiramo: 1, 00011*23, predznak: 0 0 = 0, tj. + 73

• Deljenje v plavajoči vejici – odštevanje eksponentov, deljenje mantis 74

• Konvergenčno (ali iterativno) deljenje – Newton-ova formula za iskanje ničel funkcije – Funkcija je f(x) = 1/x – b • ničla pri 1/b 75

• Algoritem (x = a/b) 1. Pomakni b za toliko mest, da velja 1 b < 2. Poišči začetni približek x 0 za 1/b (tabela). 2. Izračunaj zaporedje xi+1 = xi(2 -xib) za i=0, . . . , n-1. Dobimo xn = 1/b 3. Izračunaj produkt axn. Izvedi pomik, obraten od tistega v 1. 76