3 Modelli di reti complesse Reti random ErdosRenyi

![definizioni Rete completamente connessa [Fully connected network]: Tutti i nodi son collegati gli uni definizioni Rete completamente connessa [Fully connected network]: Tutti i nodi son collegati gli uni](https://slidetodoc.com/presentation_image_h2/b67e366eef3159fb8f526c6fa9c2419e/image-3.jpg)







![Alcune proprietà delle reti ad invarianza di scala [Scale free networks] Per n ∞ Alcune proprietà delle reti ad invarianza di scala [Scale free networks] Per n ∞](https://slidetodoc.com/presentation_image_h2/b67e366eef3159fb8f526c6fa9c2419e/image-21.jpg)


- Slides: 29

3. Modelli di reti complesse • • • Reti random (Erdos-Renyi) Reti Scale Free Costruire una ER, SF con Pajek e Octave

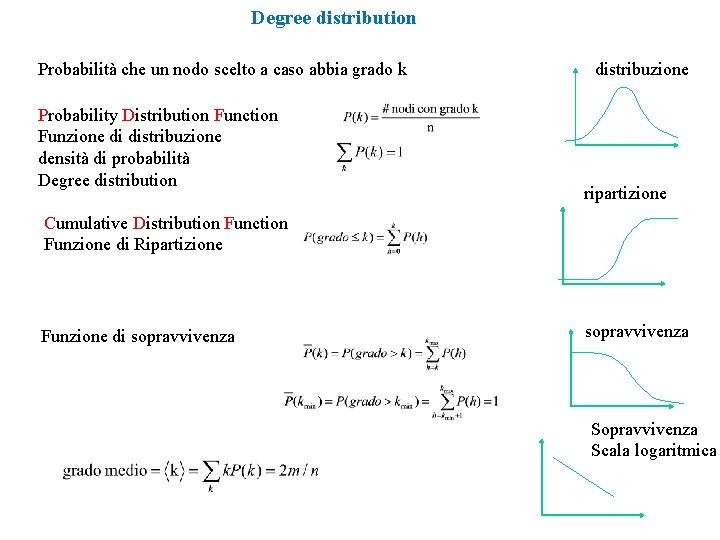
Degree distribution Probabilità che un nodo scelto a caso abbia grado k Probability Distribution Function Funzione di distribuzione densità di probabilità Degree distribution distribuzione ripartizione Cumulative Distribution Function Funzione di Ripartizione Funzione di sopravvivenza Sopravvivenza Scala logaritmica
![definizioni Rete completamente connessa Fully connected network Tutti i nodi son collegati gli uni definizioni Rete completamente connessa [Fully connected network]: Tutti i nodi son collegati gli uni](https://slidetodoc.com/presentation_image_h2/b67e366eef3159fb8f526c6fa9c2419e/image-3.jpg)
definizioni Rete completamente connessa [Fully connected network]: Tutti i nodi son collegati gli uni con gli altri Rete regolare: tutti i nodi hanno lo stesso grado Lattice: ogni nodo è collegato con i suoi vicini a seconda della distanza euclidea fissata Lattice ad anello [Ring lattice or regular ring]: i nodi sono disposti in cerchio e connessi con i k vicini più prossimi

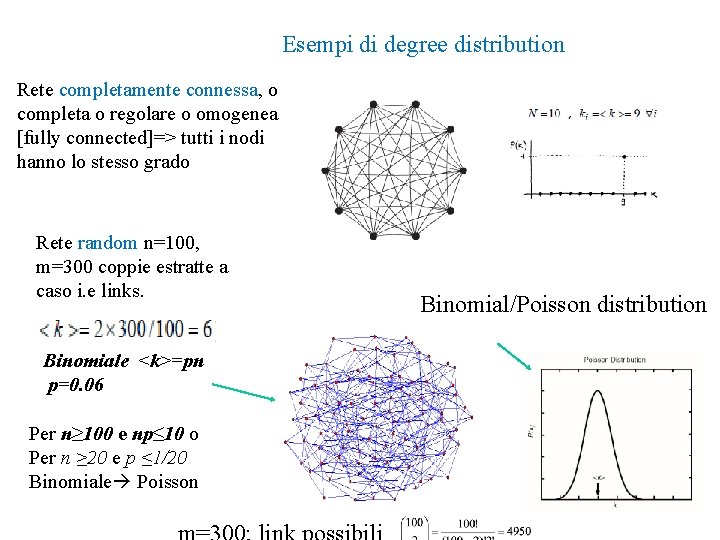
Esempi di degree distribution Rete completamente connessa, o completa o regolare o omogenea [fully connected]=> tutti i nodi hanno lo stesso grado Rete random n=100, m=300 coppie estratte a caso i. e links. Binomiale <k>=pn p=0. 06 Per n≥ 100 e np≤ 10 o Per n ≥ 20 e p ≤ 1/20 Binomiale Poisson Binomial/Poisson distribution

Reti random Una rete random è ottenuta a partire da n vertici ed aggiungendo spigoli tra essi in modo random. Diverse distribuzioni di probabilità dei gradi dei nodi corrispondono a diverse reti. Il tipo di reti random più studiato è quello in cui ogni spigolo è aggiunto con probabilità costante p. Il modello G(n, p) di Erdos-Renyi è di questo tipo. Si ottiene collegando i nodi con probabilità costante p. Il numero medio di spigoli nel modello G(n, p) è Si ottiene una distribuzione Binomiale dei gradi Nella figura seguente vediamo alcune reti Erdos-Renyi con p differenti.

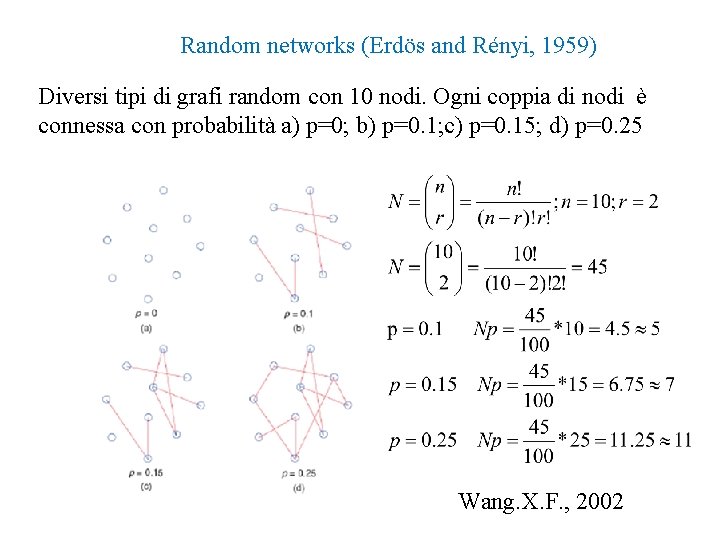
Random networks (Erdös and Rényi, 1959) Diversi tipi di grafi random con 10 nodi. Ogni coppia di nodi è connessa con probabilità a) p=0; b) p=0. 1; c) p=0. 15; d) p=0. 25 Wang. X. F. , 2002

Proprietà reti random Sopra un certo valore di p è ‘’praticamente certo’’ che il grafo sarà connesso pc (ln n)/n= percolation treshold, il grado medio corrispondente è: <kc> = 2 m/n=pc(n-1) pc n

Proprietà reti random Effetto Small World: la distanza media l Cresce lentamente co n. Il coefficiente di Clustering C tende a 0 per n ∞ (fissato <k>)

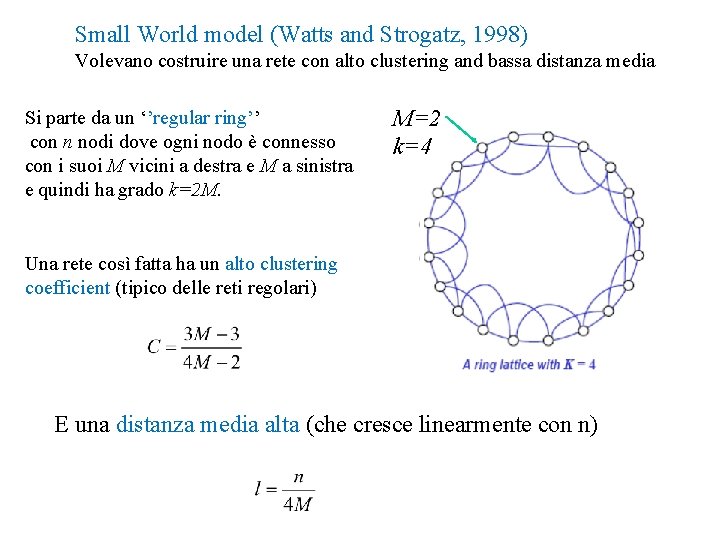
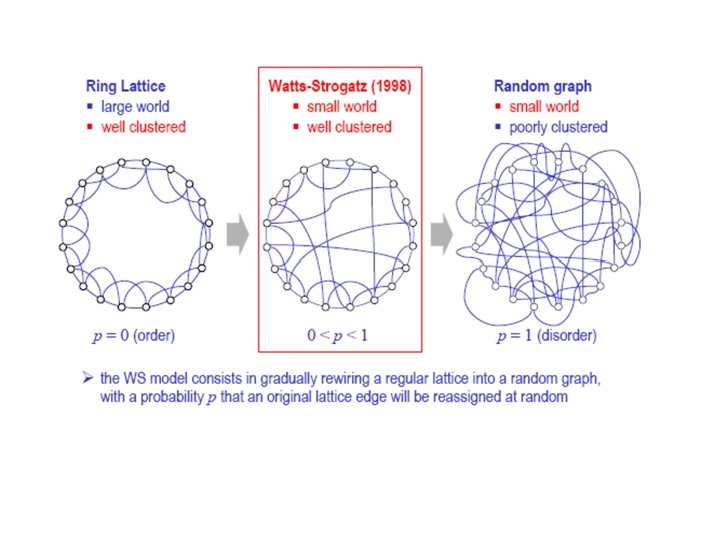
Small World model (Watts and Strogatz, 1998) Volevano costruire una rete con alto clustering and bassa distanza media Si parte da un ‘’regular ring’’ con n nodi dove ogni nodo è connesso con i suoi M vicini a destra e M a sinistra e quindi ha grado k=2 M. M=2 k=4 Una rete così fatta ha un alto clustering coefficient (tipico delle reti regolari) E una distanza media alta (che cresce linearmente con n)

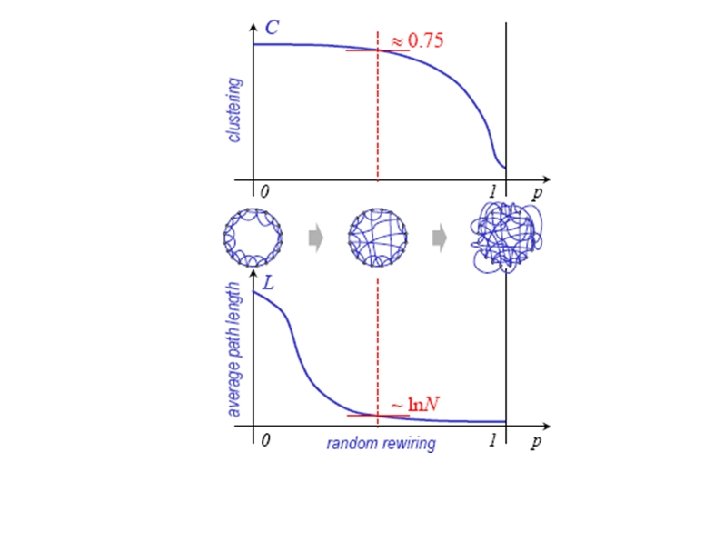
Rewiring: si fanno passare tutti i nodi da 1 a n. Si considerano tutti i link dal nodo i al suo nodo di destra j e, con probabilità p, si rompe la connessione con j e la si indirizza verso un altro nodo scelto a caso Se p è piccolo, le proprietà locali non saranno modificate in modo significativo i. e 1) la degree distribution rimarrà concentrata intorno alla media <k>=2 M 2) Il clustering coefficient C non varierà in modo significativo Ma si noterà una notevole diminuzione della distanza media che passa da a l l=n l=log(n) n



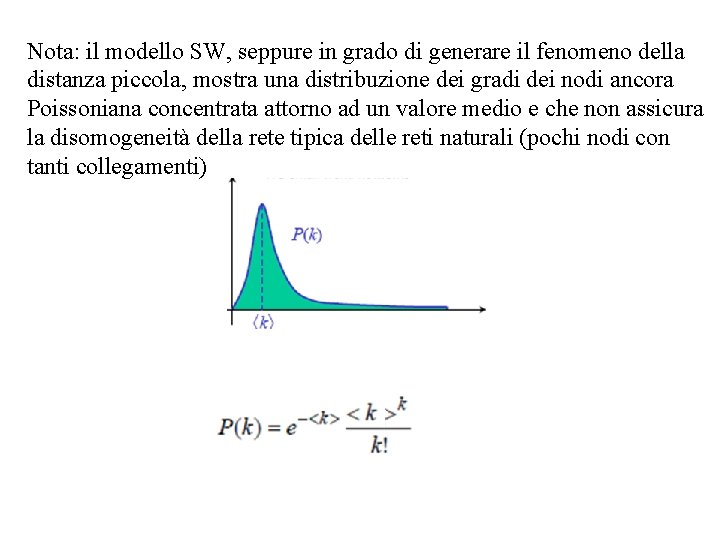
Nota: il modello SW, seppure in grado di generare il fenomeno della distanza piccola, mostra una distribuzione dei gradi dei nodi ancora Poissoniana concentrata attorno ad un valore medio e che non assicura la disomogeneità della rete tipica delle reti naturali (pochi nodi con tanti collegamenti)

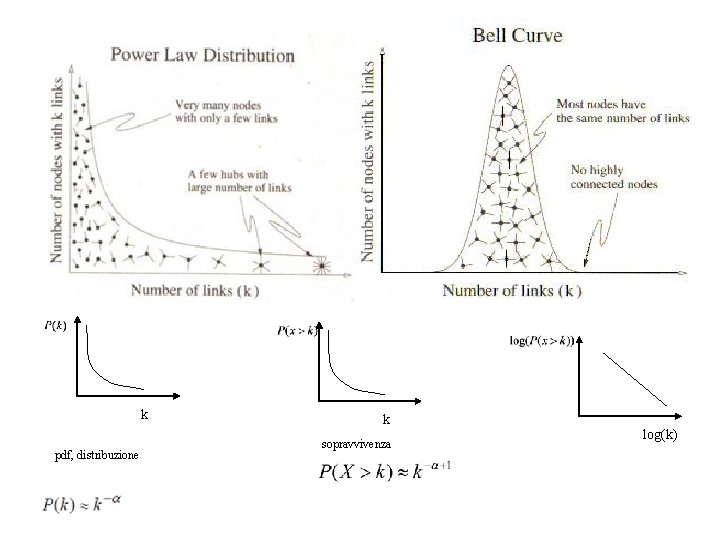
k pdf, distribuzione k sopravvivenza log(k)

Distribuzioni a legge di potenza, legge di Zipf = distribuzione ad invarianza di scala distribuzione di Pareto La funzione di sopravvivenza ha la forma Di solito sono rappresentate in un grafico log-log cioè: E la relazione diventa lineare L’economista Pareto la individuò nella distribuzione del reddito. Il linguista Zipf la individuò nella frequenza d’uso delle parole nei testi. Principio 80/20: il 20% della popolazione detiene l’ 80% della ricchezza. Nonostante siano molti i fenomeni che presentano distribuzioni ad invarianza di scala per alcuni intervalli, sono rari i casi in cui questo valga lungo tutto il supporto.

Commenti sulla legge di potenza http: //www. nexres. org/2009/04/27/distribuzione-a-legge-dipotenza/ http: //www. cash-cow. it/2007/scienza-della-complessita/legge-dipotenza. htm

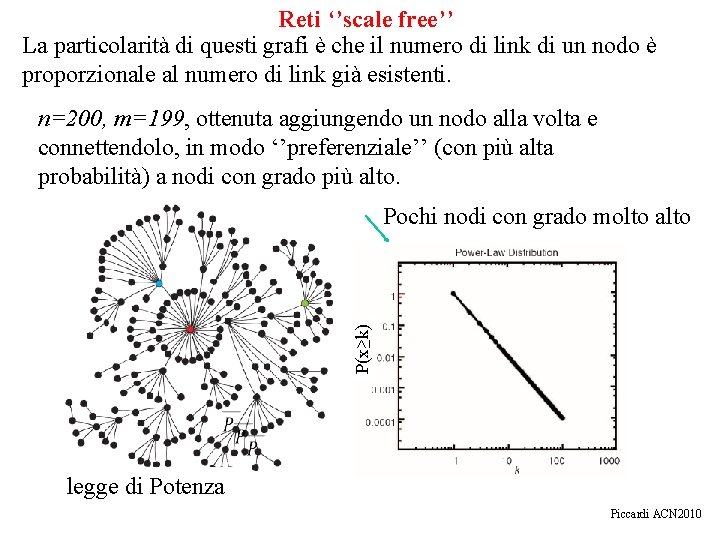
Reti ‘’scale free’’ La particolarità di questi grafi è che il numero di link di un nodo è proporzionale al numero di link già esistenti. n=200, m=199, ottenuta aggiungendo un nodo alla volta e connettendolo, in modo ‘’preferenziale’’ (con più alta probabilità) a nodi con grado più alto. P(x≥k) Pochi nodi con grado molto alto legge di Potenza Piccardi ACN 2010

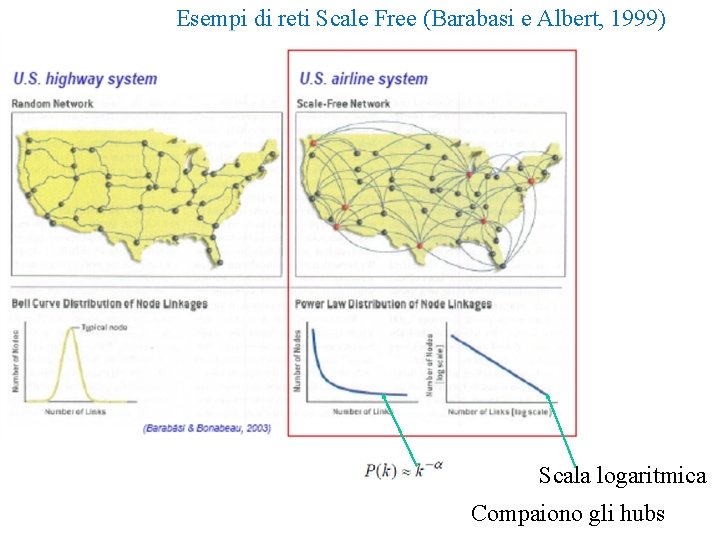
Esempi di reti Scale Free (Barabasi e Albert, 1999) Scala logaritmica Compaiono gli hubs

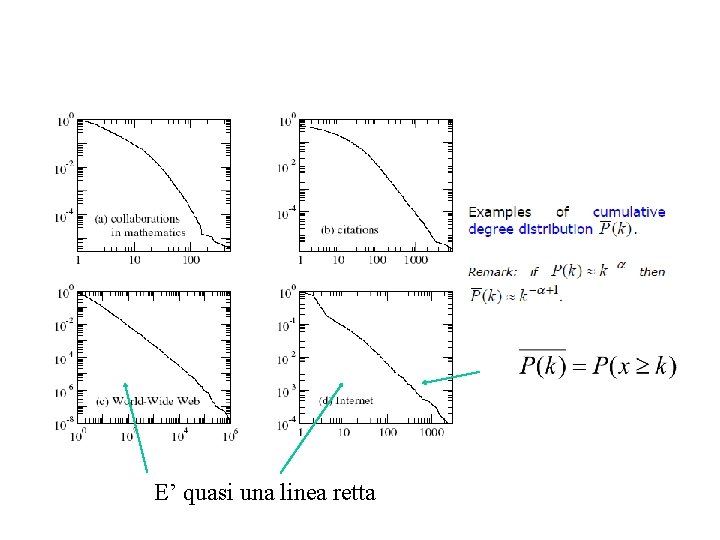
E’ quasi una linea retta

Costruire una scale-free network Algoritmo di Barabasi and Albert (1999) ispirato alla crescita della rete WWW 1. Si considerano m 0 nodi connessi in modo arbitrario (ad esempio una random network) 2. Ad ogni passo, si aggiunge un nuovo nodo i con m≤m 0 links in modo che si attacchi ai nodi esistenti a seconda del loro grado. 3. Preferential attachment: gli m links si legano con più alta probabilità a nodi con alto grado ( «rich get richer» ) La probabilità di collegare un nuovo nodo i ad uno esistente j è proporzionale a kj:
![Alcune proprietà delle reti ad invarianza di scala Scale free networks Per n Alcune proprietà delle reti ad invarianza di scala [Scale free networks] Per n ∞](https://slidetodoc.com/presentation_image_h2/b67e366eef3159fb8f526c6fa9c2419e/image-21.jpg)
Alcune proprietà delle reti ad invarianza di scala [Scale free networks] Per n ∞ 1) Il grado medio tende a <k>=2 m e P(k)=k -3 2) La varianza <k 2>= 2=<k 2>-<k> 2 diverge (‘’heavy tail’’). la varianza continua ad aumentare se aumento il numero di nodi 3) La distanza media aumenta come World’’) (‘’ultra Small 4) Il clustering C 0 ma meno velocemente rispetto alle reti E-R dove è molto piccolo per qualsiasi n

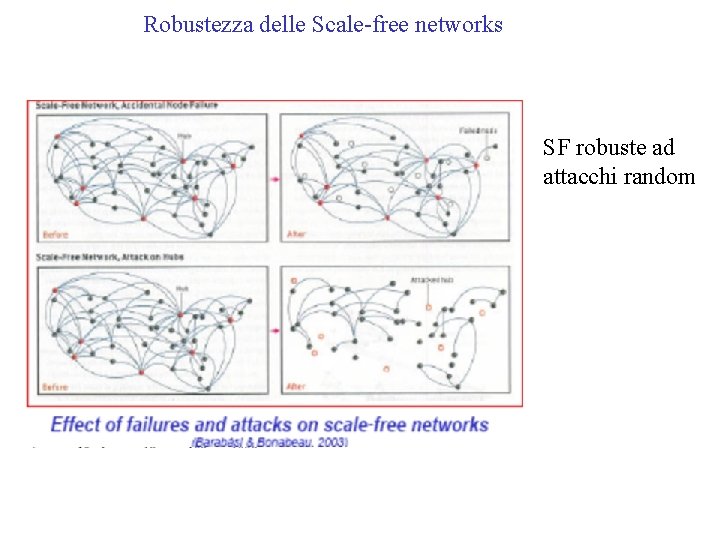
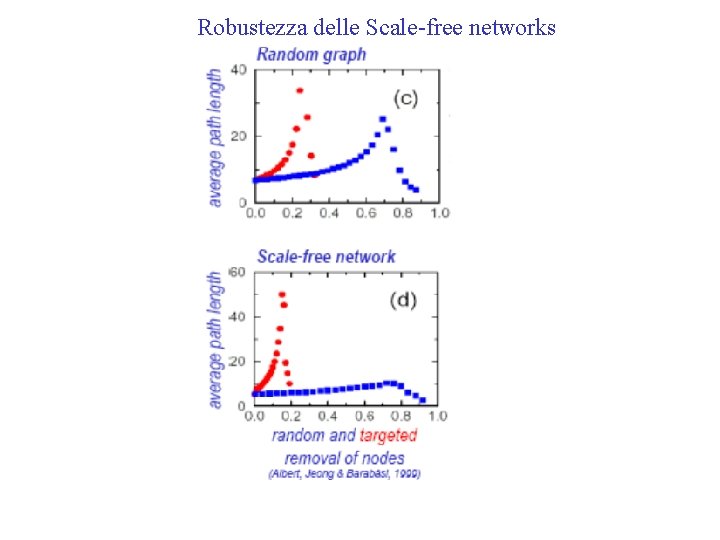
Robustezza delle Scale-free networks SF robuste ad attacchi random

Robustezza delle Scale-free networks

Proprietà reti scale Free Legge di potenza disomogenea Alto clustering Presenza di Hub Robustezza ad attacchi casuali Vulnerabilità ad attacchi mirati Descrivono Internet WWW Servizi urbani Traffico aereo Reti sociali Lo shortest path dipende dalla distanza di un hub

Varie

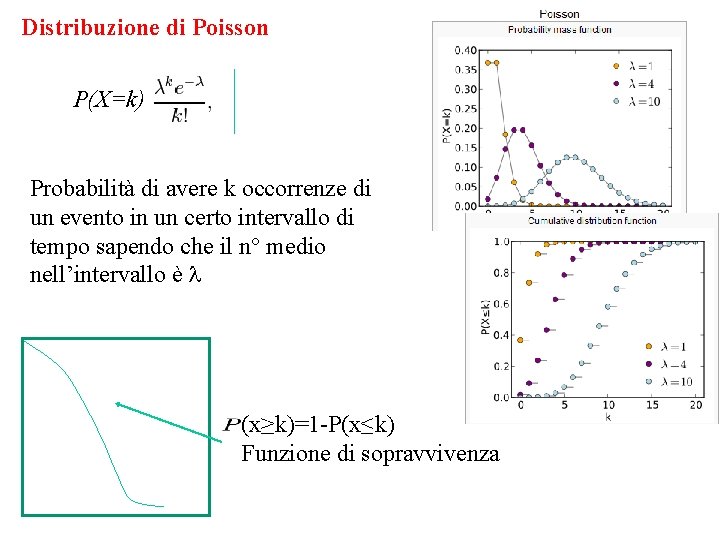
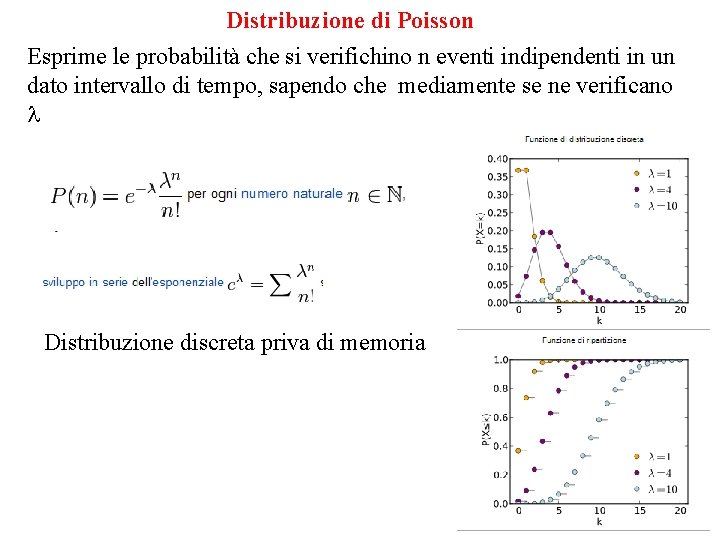
Distribuzione di Poisson P(X=k) Probabilità di avere k occorrenze di un evento in un certo intervallo di tempo sapendo che il n° medio nell’intervallo è l (x≥k)=1 -P(x≤k) Funzione di sopravvivenza

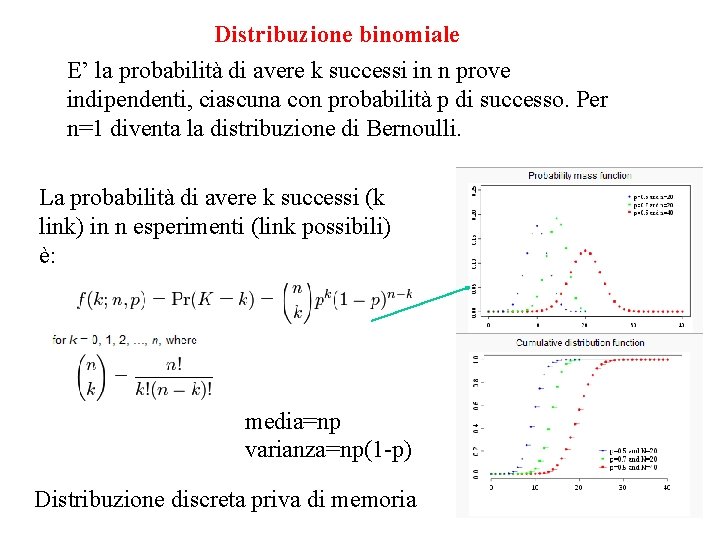
Distribuzione binomiale E’ la probabilità di avere k successi in n prove indipendenti, ciascuna con probabilità p di successo. Per n=1 diventa la distribuzione di Bernoulli. La probabilità di avere k successi (k link) in n esperimenti (link possibili) è: media=np varianza=np(1 -p) Distribuzione discreta priva di memoria

Distribuzione di Poisson Esprime le probabilità che si verifichino n eventi indipendenti in un dato intervallo di tempo, sapendo che mediamente se ne verificano l Distribuzione discreta priva di memoria

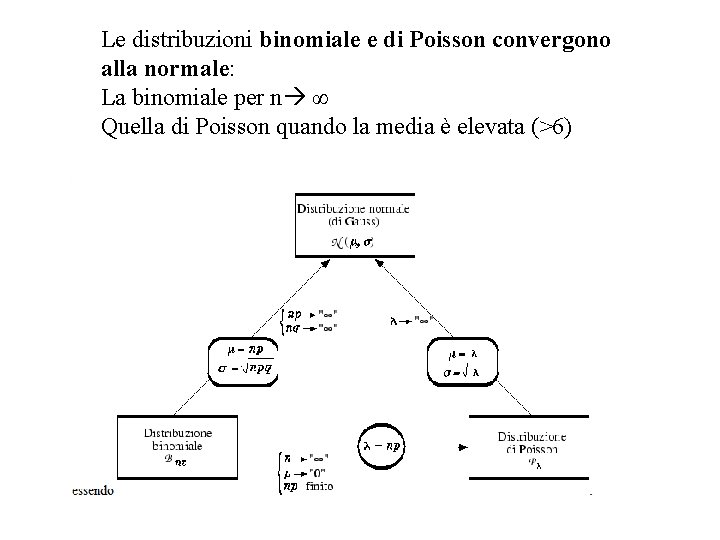
Le distribuzioni binomiale e di Poisson convergono alla normale: La binomiale per n ∞ Quella di Poisson quando la media è elevata (>6)