Random Variables and Probability Distributions Random Variables Random

Random Variables and Probability Distributions • Random Variables - Random responses corresponding to subjects randomly selected from a population. • Probability Distributions - A listing of the possible outcomes and their probabilities (discrete r. v. s) or their densities (continuous r. v. s) • Normal Distribution - Bell-shaped continuous distribution widely used in statistical inference • Sampling Distributions - Distributions corresponding to sample statistics (such as mean and proportion) computed from random samples

Normal Distribution • Bell-shaped, symmetric family of distributions • Classified by 2 parameters: Mean (m) and standard deviation (s). These represent location and spread • Random variables that are approximately normal have the following properties wrt individual measurements: – – Approximately half (50%) fall above (and below) mean Approximately 68% fall within 1 standard deviation of mean Approximately 95% fall within 2 standard deviations of mean Virtually all fall within 3 standard deviations of mean • Notation when Y is normally distributed with mean m and standard deviation s :

Normal Distribution
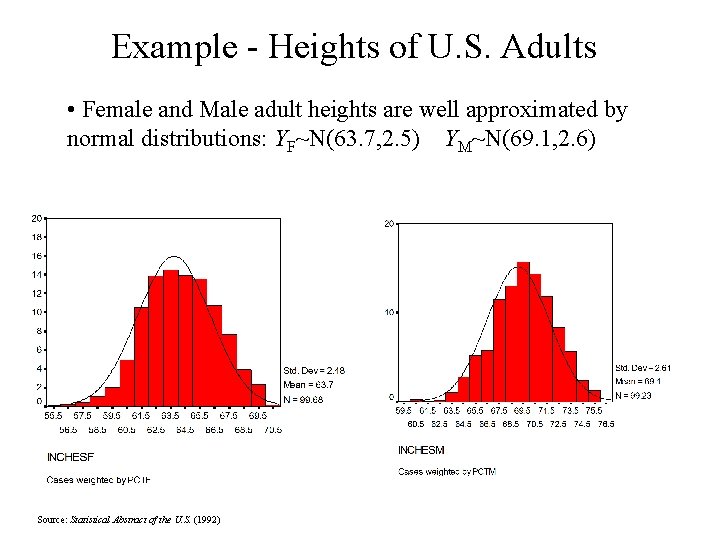
Example - Heights of U. S. Adults • Female and Male adult heights are well approximated by normal distributions: YF~N(63. 7, 2. 5) YM~N(69. 1, 2. 6) Source: Statistical Abstract of the U. S. (1992)

Standard Normal (Z) Distribution • Problem: Unlimited number of possible normal distributions (- < m < , s > 0) • Solution: Standardize the random variable to have mean 0 and standard deviation 1 • Probabilities of certain ranges of values and specific percentiles of interest can be obtained through the standard normal (Z) distribution

Standard Normal (Z) Distribution • Standard Normal Distribution Characteristics: – – P(Z 0) = P(Y m ) = 0. 5000 P(-1 Z 1) = P(m-s Y m+s ) = 0. 6826 P(-2 Z 2) = P(m-2 s Y m+2 s ) = 0. 9544 P(Z za) = P(Z -za) = a (using Z-table)

Finding Probabilities of Specific Ranges • Step 1 - Identify the normal distribution of interest (e. g. its mean (m) and standard deviation (s) ) • Step 2 - Identify the range of values that you wish to determine the probability of observing (YL , YU), where often the upper or lower bounds are or - • Step 3 - Transform YL and YU into Z-values: • Step 4 - Obtain P(ZL Z ZU) from Z-table

Example - Adult Female Heights • What is the probability a randomly selected female is 5’ 10” or taller (70 inches)? • Step 1 - Y ~ N(63. 7 , 2. 5) • Step 2 - YL = 70. 0 YU = • Step 3 - • Step 4 - P(Y 70) = P(Z 2. 52) =. 0059 ( 1/170)

Finding Percentiles of a Distribution • Step 1 - Identify the normal distribution of interest (e. g. its mean (m) and standard deviation (s) ) • Step 2 - Determine the percentile of interest 100 p% (e. g. the 90 th percentile is the cut-off where only 90% of scores are below and 10% are above) • Step 3 - Turn the percentile of interest into a tail probability a and corresponding z-value (zp): – If 100 p 50 then a = 1 -p and zp = za – If 100 p < 50 then a = p and zp = -za • Step 4 - Transform zp back to original units:

Example - Adult Male Heights • • Above what height do the tallest 5% of males lie above? Step 1 - Y ~ N(69. 1 , 2. 6) Step 2 - Want to determine 95 th percentile (p =. 95) Step 3 - Since 100 p > 50, a = 1 -p = 0. 05 zp = za = z. 05 = 1. 645 • Step 4 - Y. 95 = 69. 1 + (1. 645)(2. 6) = 73. 4

Statistical Models • When making statistical inference it is useful to write random variables in terms of model parameters and random errors • Here m is a fixed constant and e is a random variable • In practice m will be unknown, and we will use sample data to estimate or make statements regarding its value

Sampling Distributions and the Central Limit Theorem • Sample statistics based on random samples are also random variables and have sampling distributions that are probability distributions for the statistic (outcomes that would vary across samples) • When samples are large and measurements independent then many estimators have normal sampling distributions (CLT): – Sample Mean: – Sample Proportion:

Example - Adult Female Heights • Random samples of n = 100 females to be selected • For each sample, the sample mean is computed • Sampling distribution: • Note that approximately 95% of all possible random samples of 100 females will have sample means between 63. 0 and 64. 0 inches
- Slides: 13