2 5 FRACTIONS PARTIELLES cours 13 Au dernier








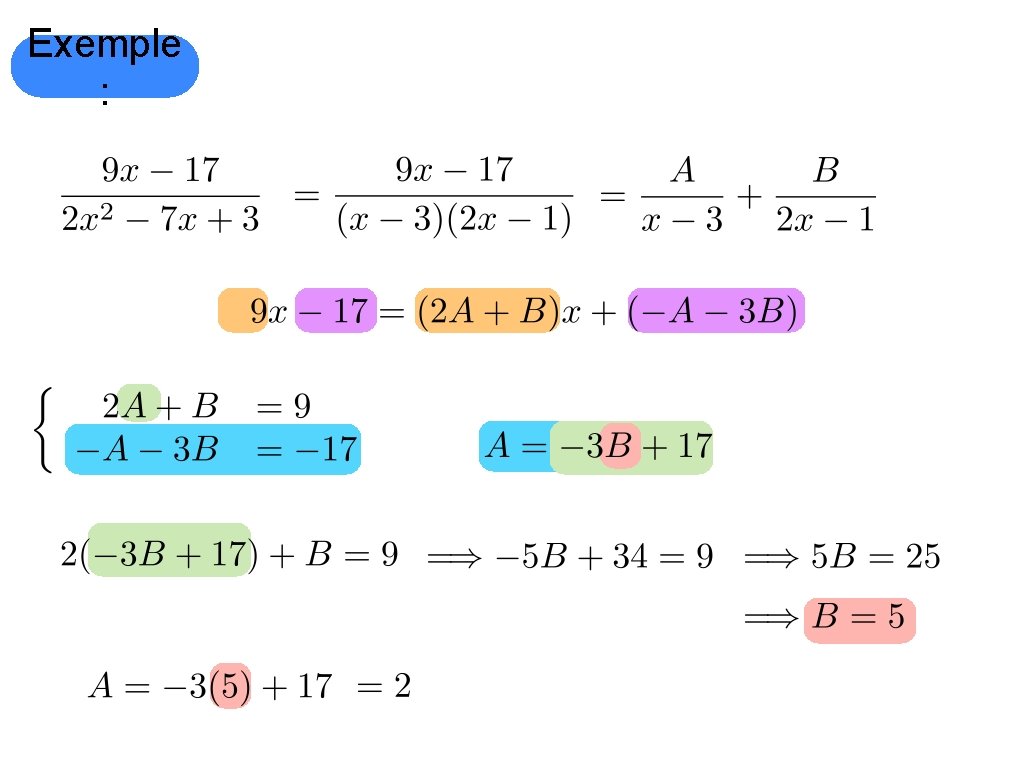
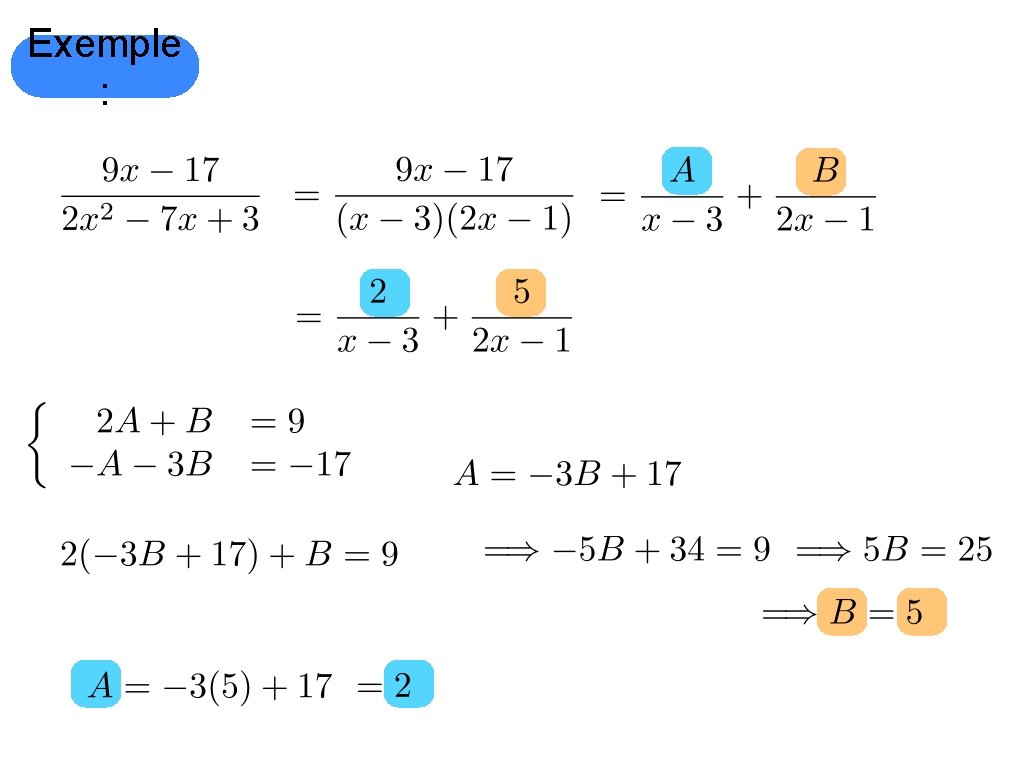












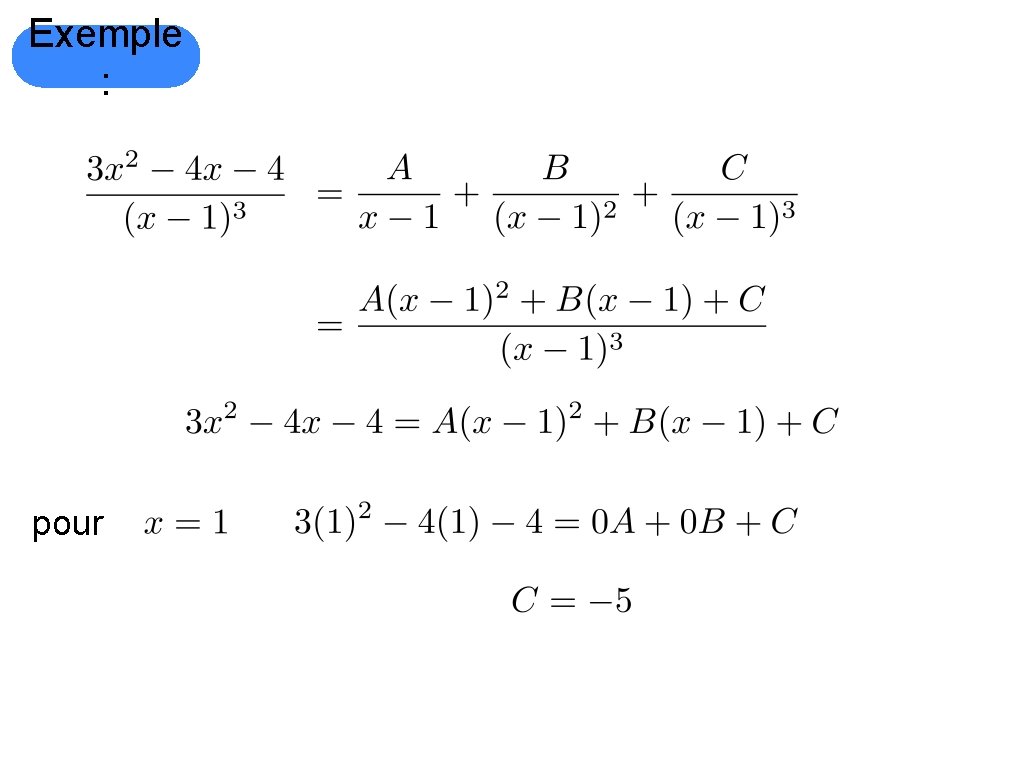
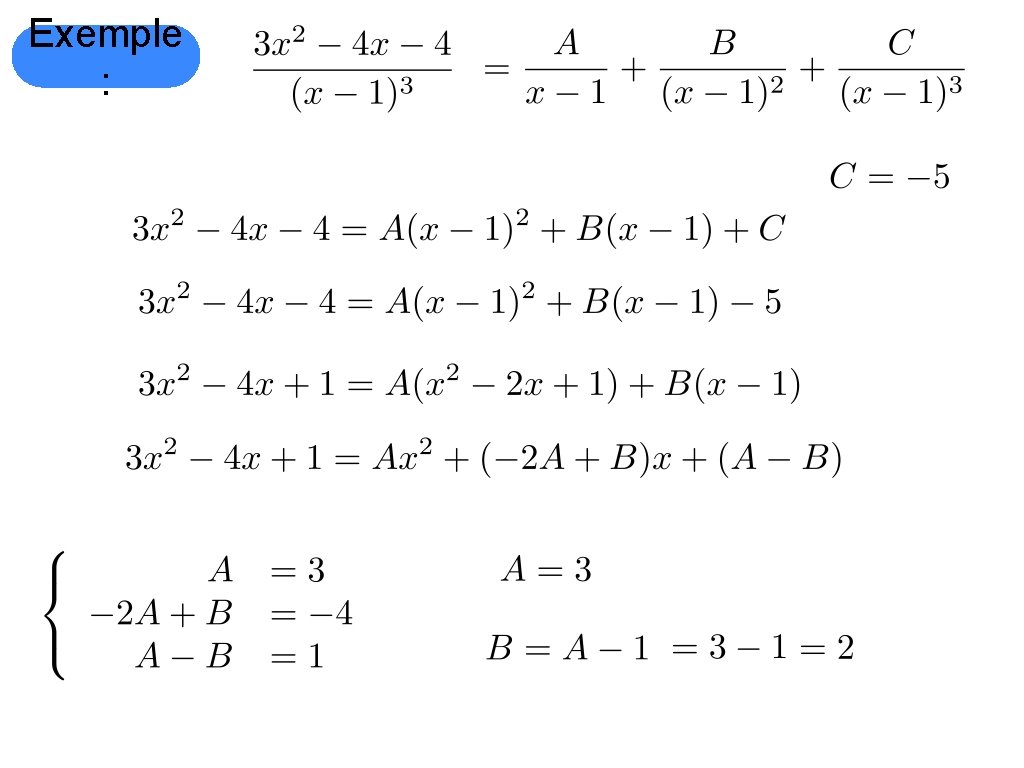
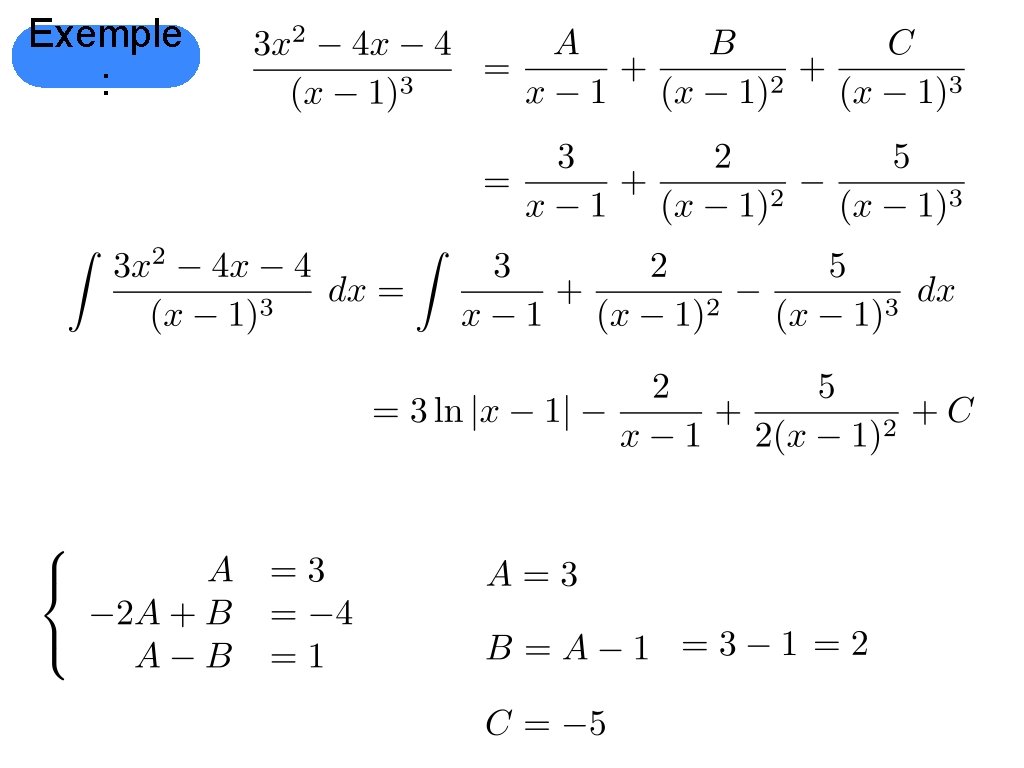





- Slides: 32

2. 5 FRACTIONS PARTIELLES cours 13

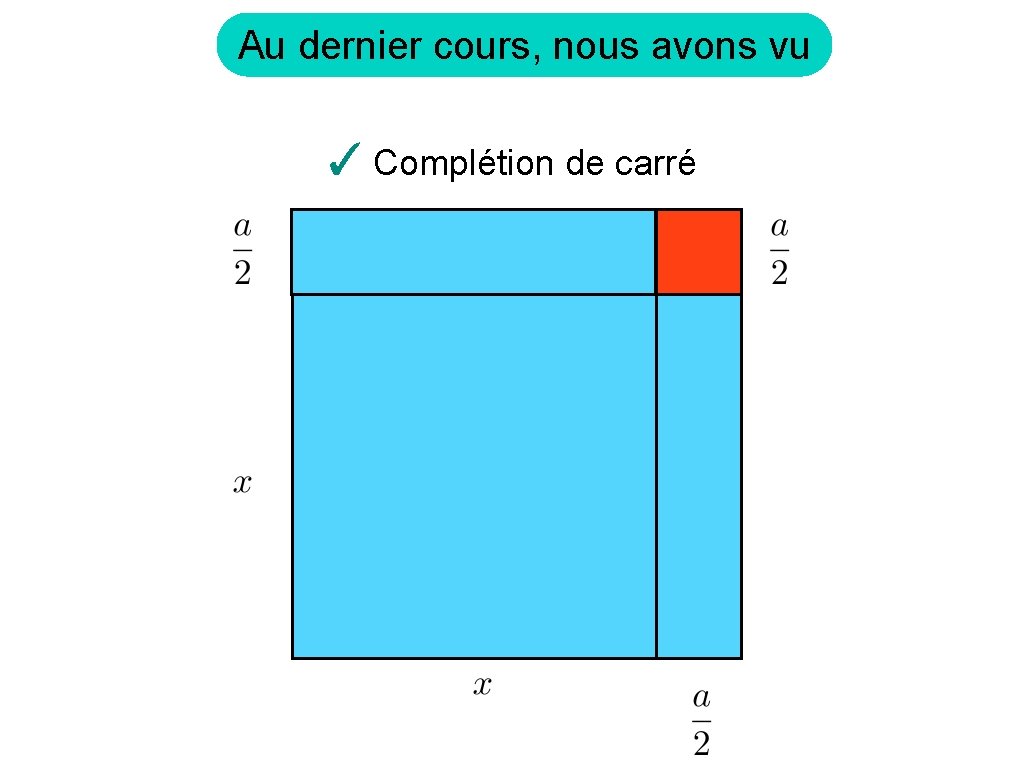
Au dernier cours, nous avons vu ✓ Complétion de carré

Aujourd’hui, nous allons voir ✓ Comment faire le processus inverse de mettre sur le même dénominateur.

On peut calculer une intégrale de la forme en faisant un changement de variable. On peut aussi calculer une intégrale de la forme en faisant une complétion de carré suivi d’une substitution trigonométrique.

Est-ce possible d’intégrer n’importe quelle fonction de la forme ? Pour résoudre ce problème, on va essayer de ramener ce quotient polynomial aux deux formes qu’on sait intégrer.


Comment faire le processus inverse de mettre sur le même dénominateur ? Si on a une expression de la forme où et polynômes sont des Si le degré de est plus grand ou égale que le degré de , on fait une division polynomiale.

Pour faire le processus inverse de mettre sur le même dénominateur, la première chose à faire est de déterminer quels étaient les dénominateurs initiaux. Pour faire ça, il faut complètement factoriser le dénominateur.

Exemple : et

Exemple : Dans une égalité polynomiale, les coefficients de chaque puissance de x doivent être égaux.
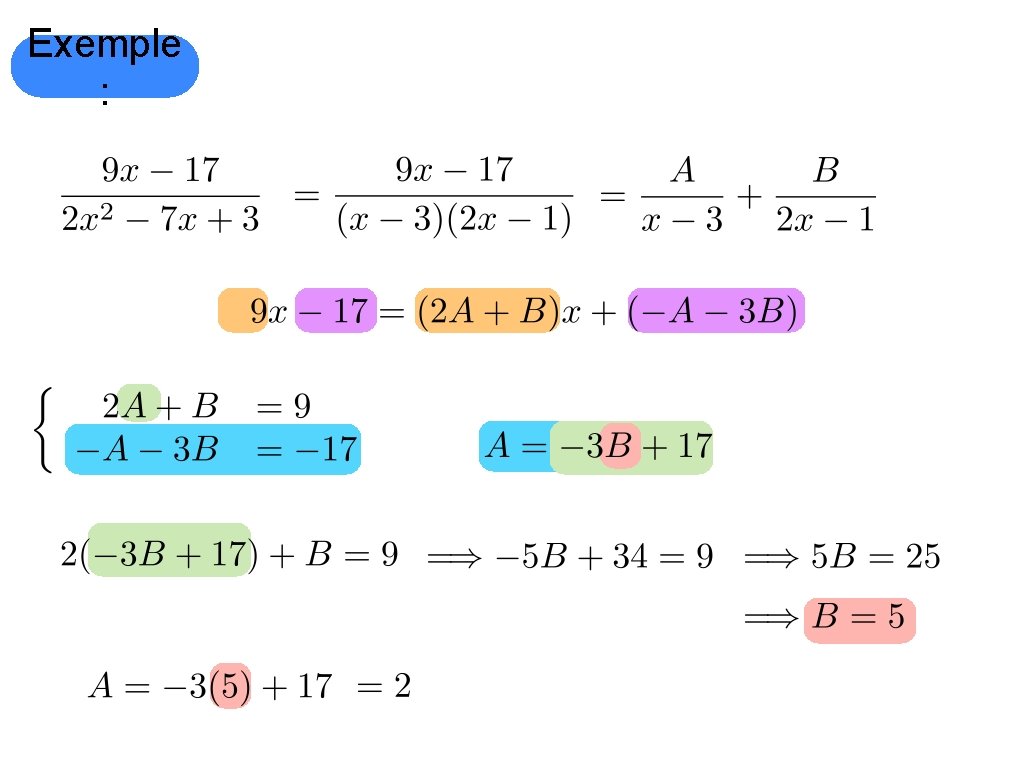
Exemple :
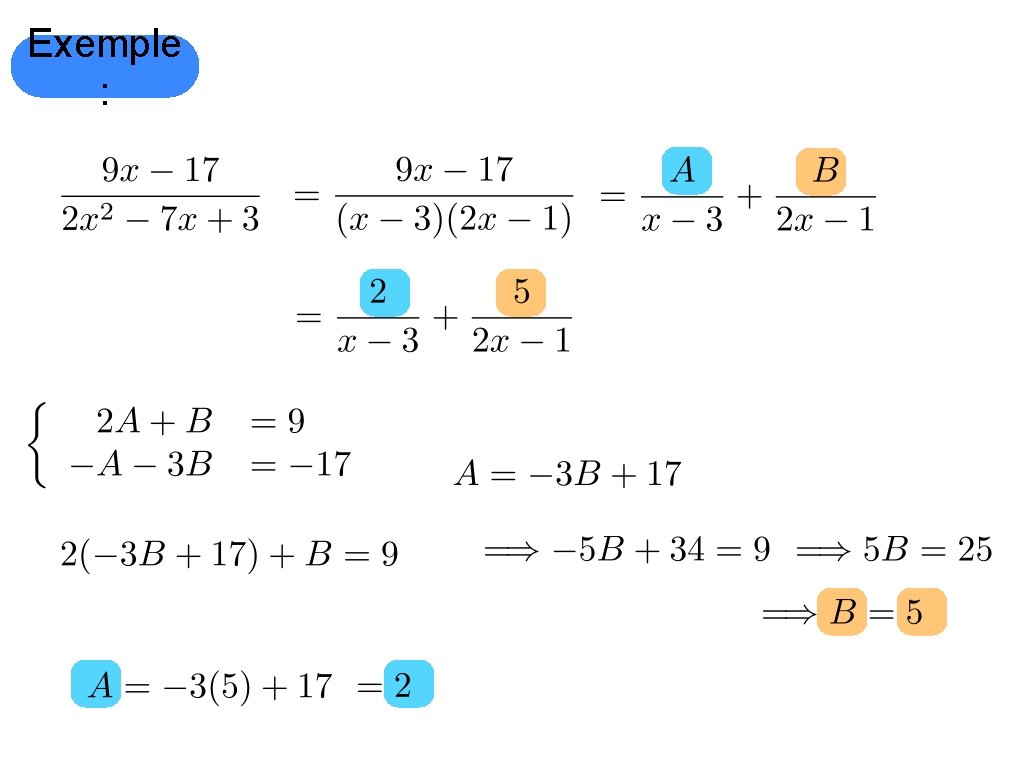
Exemple :

Exemple : (Prise 2) Cette égalité doit être vraie pour toute valeur de

Exemple : (Prise 2) Cette égalité doit être vraie pour toute valeur de Pour

Faites les exercices suivants Section 2, # 19 a), b), 20 a)

Vous avez probablement déjà vu le théorème suivant: Théorème: Soit un polynôme, C’est-à-dire est un zéro du polynôme si et seulement si est un facteur du polynôme.

On peut donc conclure que certains polynômes ne peuvent pas être factorisés en facteur linéaire. Mais Donc ne peut pas être factorisé.

Exemple : Pour

Exemple :

Exemple :

Exemple :

Exemple :

Faites les exercices suivants Section 2, # 19 c), d), 20 g)

Si un des facteurs du dénominateur apparait plus d’une fois Exemple : Nous mène nulle part, car ce polynôme n’est pas un multiple de ce polynôme.
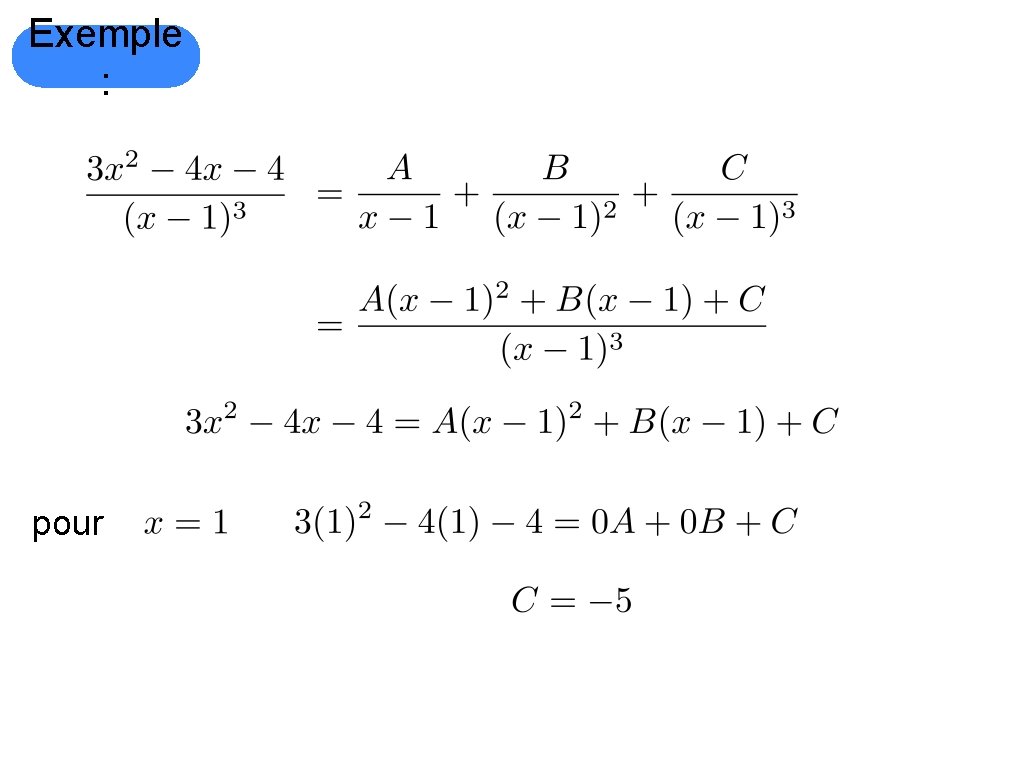
Exemple : pour
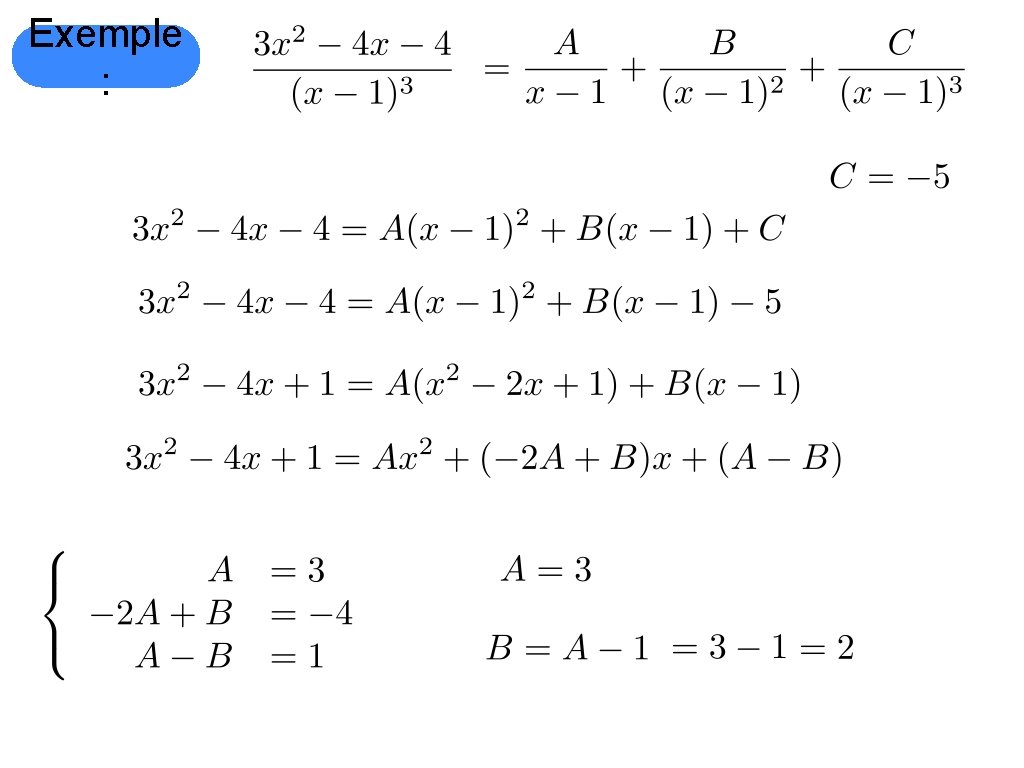
Exemple :
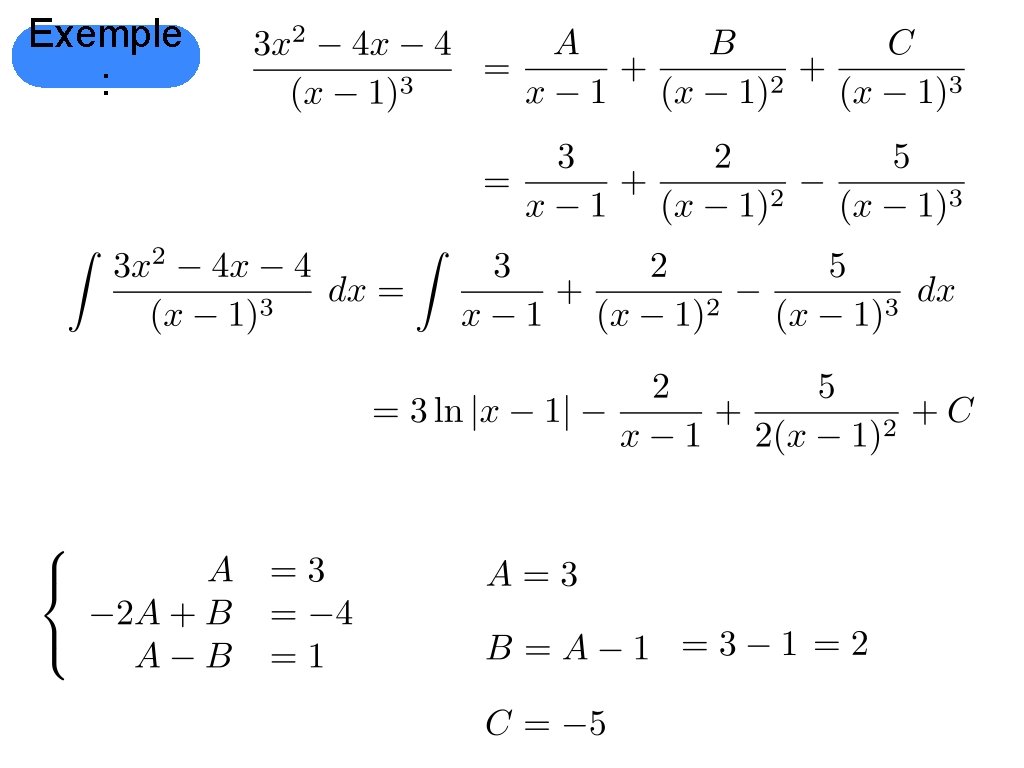
Exemple :

Faites les exercices suivants Section 2, # 19 e), f), 20 f)

Les numérateurs des termes linéaires sont des constantes. Les numérateurs des termes du deuxième degré sont des termes linaire. Les termes qui apparaissent avec multiplicité feront apparaitre autant de termes dans la somme que la multiplicité.

Faites les exercices suivants Section 2, # 20

Aujourd’hui, nous avons vu ✓ Fractions partielles

Devoir: Section 2 # 19 à 21
 Cours e marketing
Cours e marketing Cned espace inscrit
Cned espace inscrit Aéraulique cours
Aéraulique cours Crise biologique
Crise biologique La tectonique des plaques - cours
La tectonique des plaques - cours Cours anthropologie infirmier
Cours anthropologie infirmier Viande maturée danger
Viande maturée danger Assemblage en cours
Assemblage en cours Les helminthes cours
Les helminthes cours Psychologie expérimentale - cours
Psychologie expérimentale - cours Méthode croc
Méthode croc Gestion internationale des ressources humaines cours
Gestion internationale des ressources humaines cours Musibiol exercice
Musibiol exercice Syllabus de cours
Syllabus de cours La fin de la semaine prochaine
La fin de la semaine prochaine Fdf 3
Fdf 3 Cours dynatrace
Cours dynatrace Equilibre alimentaire ifsi
Equilibre alimentaire ifsi Cours hydrogéologie master
Cours hydrogéologie master Zonecourshec
Zonecourshec Repère orthonormé vierge
Repère orthonormé vierge Cours virtualisation
Cours virtualisation Cours mcd
Cours mcd Intégrale impropre cours
Intégrale impropre cours Filtrage numérique cours
Filtrage numérique cours Cours den
Cours den Pharmacodynamie ifsi
Pharmacodynamie ifsi Cours turbomachine
Cours turbomachine Cours mimo
Cours mimo Cours cap apr
Cours cap apr Représentation chromatique des nombres
Représentation chromatique des nombres Université constantine 3 faculté de médecine
Université constantine 3 faculté de médecine Transistor dynamique
Transistor dynamique