15 499 Algorithms and Applications Error Correcting Codes

15 -499: Algorithms and Applications Error Correcting Codes – III - Expander graphs - Tornado codes - Expander codes 15 -499 1

Why Tornado Codes? • Desgined by Luby, Mitzenmacher, Shokrollahi et al • Forward Error Correction like RS & Linear codes • The other two give nearly optimal rates • But they are slow : Code Encoding Decoding Linear O(n 2) O(n 3) RS O(n log n) O(n 2) Tornado O(n log 1/e) 15 -499 2

The idea behind Tornado codes • Easy coding/decoding: linear codes with explicit construction • Fast coding/decoding: each check bit depends on only a few message bits 15 -499 3

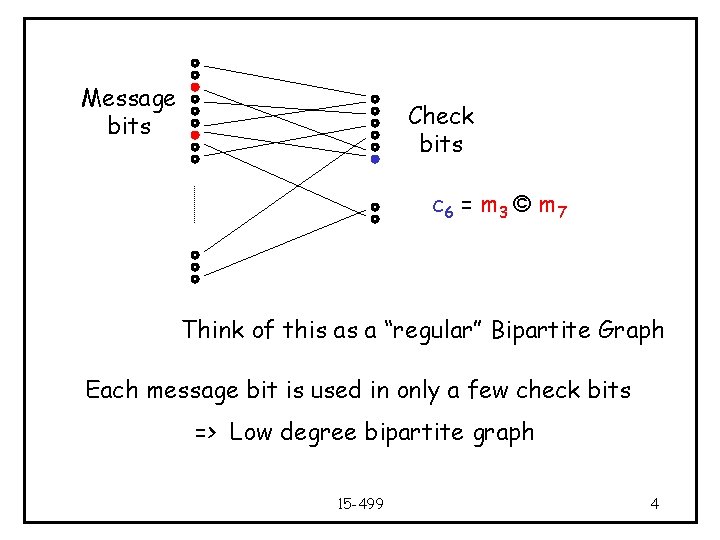
Message bits Check bits c 6 = m 3 © m 7 Think of this as a “regular” Bipartite Graph Each message bit is used in only a few check bits => Low degree bipartite graph 15 -499 4

Properties of a good code • There should be “few” check bits • Linear time encoding – Average degree on the left should be a small constant • Easy error detection/decoding – Each set of message bits should influence many check bits – Existence of unshared neighbors 15 -499 5

Outline • Expander Graphs – Applications – Properties – Constructions • Tornado Codes – Encoding/Decoding Algorithms – Brief Analysis • Expander Codes – Construction – Brief Analysis 15 -499 6

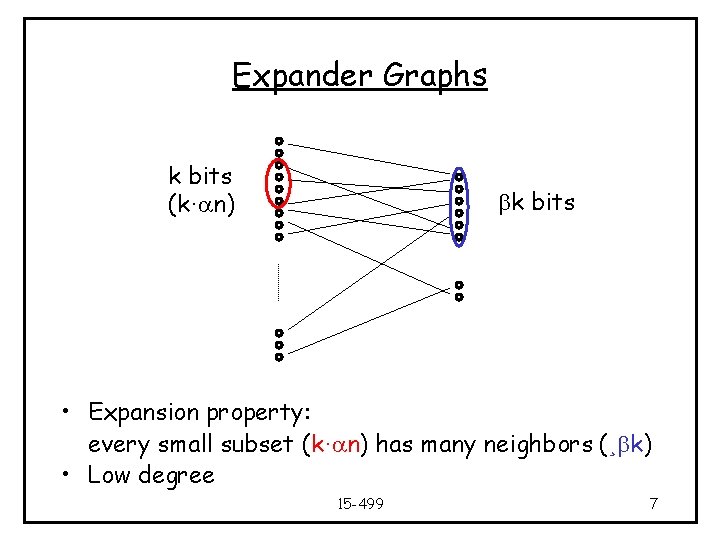
Expander Graphs k bits (k·an) bk bits • Expansion property: every small subset (k·an) has many neighbors (¸bk) • Low degree 15 -499 7

Expander Graphs: Applications • Pseudo-randomness (Derandomization) • Error Correcting Codes • Communication networks – Peer-to-peer networks – Gossip based protocols – Loss-resilient networks 15 -499 8

Expander Graphs: Properties • Expanders are “pseudo-random” objects • If we start at a node and wander around randomly, in a short while, we can reach any part of the graph • Expander-based codes behave like random linear codes, but have fast constructions. 15 -499 9

Expander Graphs: Properties • Expansion can be characterized using the eigenvaules of the graph • A = normalized adjacency matrix • Maximum eigenvalue is 1. (Why? ) • Think of the eigenvectors as probability distributions • Second largest eigenvalue is an indicator of expansion – the smaller the better 15 -499 10

Expander Graphs: Properties • Prob. Dist. – p ; Uniform dist. – u • Small |p-u| indicates a large amount of “randomness” • Show that |Ap-u| · l 2|p-u| • Therefore small l 2 => fast convergence to uniform • Expansion b ¼ (1/l 2)2 15 -499 11

Expander Graphs: Properties • To show that |Ap-u| · l 2|p-u| • Let p = u + p’ • u is the principle eigenvector • p’ is perpendicular to u Au = u Ap’ · l 2 p’ • So, Ap · u + l 2 p’ • Thus, |Ap - u| · l 2|p’| 15 -499 12

Expander Graphs: Constructions • Important parameters – size, degree, expansion • Randomized constructions – A random d-regular graph is an expander with a high probability – Choose d random perfect matchings – Time consuming and cannot be stored compactly • Explicit constructions – Cayley graphs, Ramanujan graphs etc – Typical technique – start with a small expander, apply operations to increase its size 15 -499 13

Expander Graphs: Constructions • Start with a small expander, and apply operations to make it bigger while preserving expansion • Squaring – G 2 contains edge (u, w) if G contains edges (u, v) and (v, w) for some node v – A’ = A 2 – 1/d I – l’ = l 2 – 1/d Size – d’ = d 2 - d Degree Expansion 15 -499 14

Expander Graphs: Constructions • Start with a small expander, and apply operations to make it bigger while preserving expansion • Tensor Product – G = Ax. B nodes are (a, b) 8 a 2 A and b 2 B – edge between (a, b) and (a’, b’) if A contains (a, a’) and B contains (b, b’) – n’ = n 1 n 2 Size – l’ = max (l 1, l 2) Degree – d’ = d 1 d 2 Expansion 15 -499 15

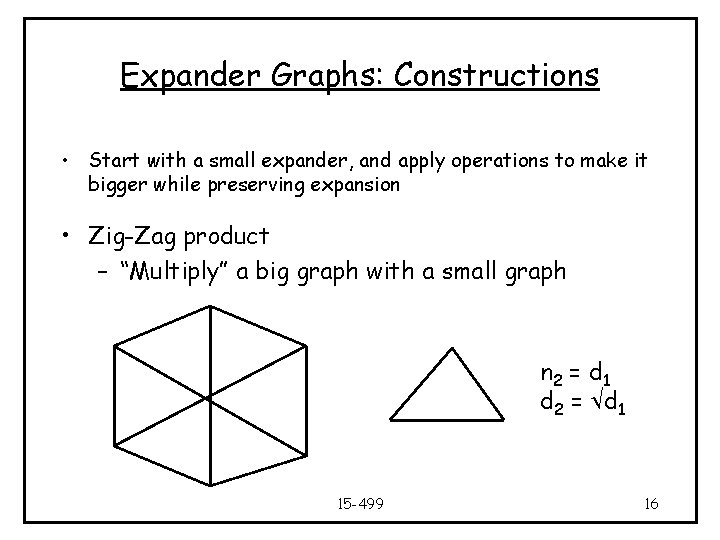
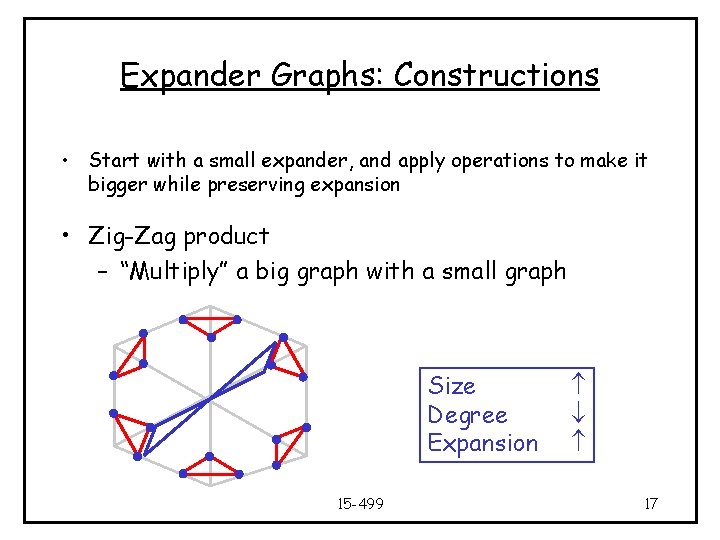
Expander Graphs: Constructions • Start with a small expander, and apply operations to make it bigger while preserving expansion • Zig-Zag product – “Multiply” a big graph with a small graph n 2 = d 1 d 2 = d 1 15 -499 16

Expander Graphs: Constructions • Start with a small expander, and apply operations to make it bigger while preserving expansion • Zig-Zag product – “Multiply” a big graph with a small graph Size Degree Expansion 15 -499 17

Outline ü Expander Graphs – Applications – Properties – Constructions • Tornado Codes – Encoding/Decoding Algorithms – Brief Analysis • Expander Codes – Construction – Brief Analysis 15 -499 18

The loss model • Random Erasure Model: Each bit is lost independently with some probability m • We know the positions of the lost bits • Error Correction can be done with some more effort 15 -499 19

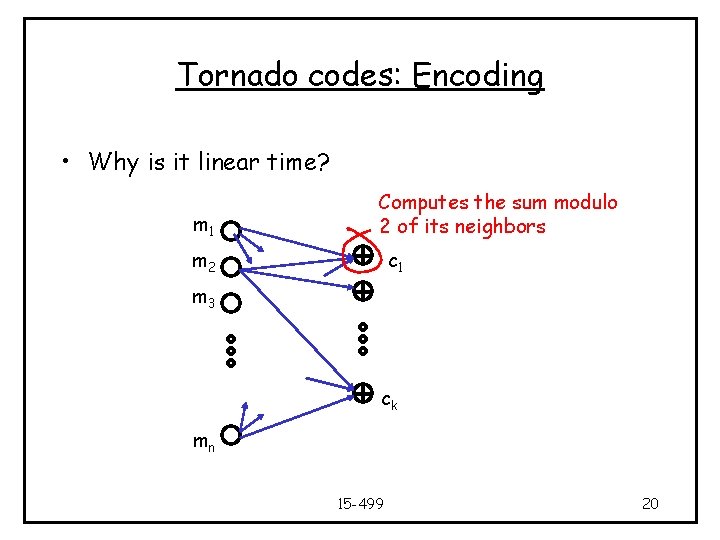
Tornado codes: Encoding • Why is it linear time? m 1 Computes the sum modulo 2 of its neighbors m 2 c 1 m 3 ck mn 15 -499 20

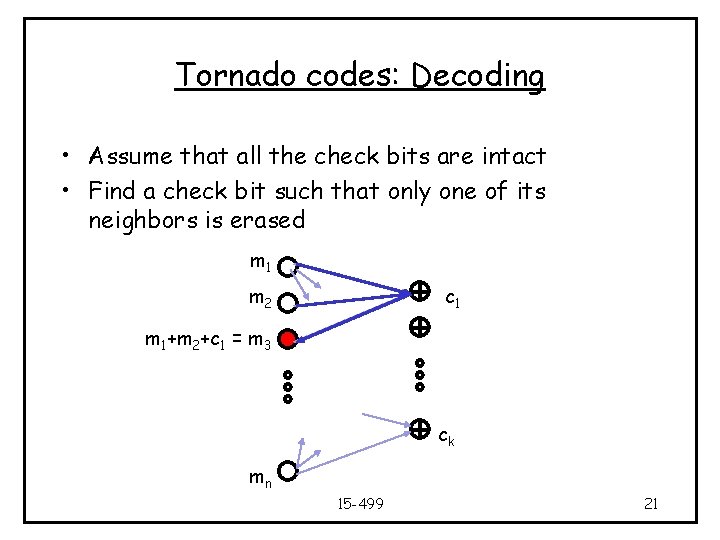
Tornado codes: Decoding • Assume that all the check bits are intact • Find a check bit such that only one of its neighbors is erased m 1 m 2 c 1 m 1+m 2+c 1 = m 3 ck mn 15 -499 21

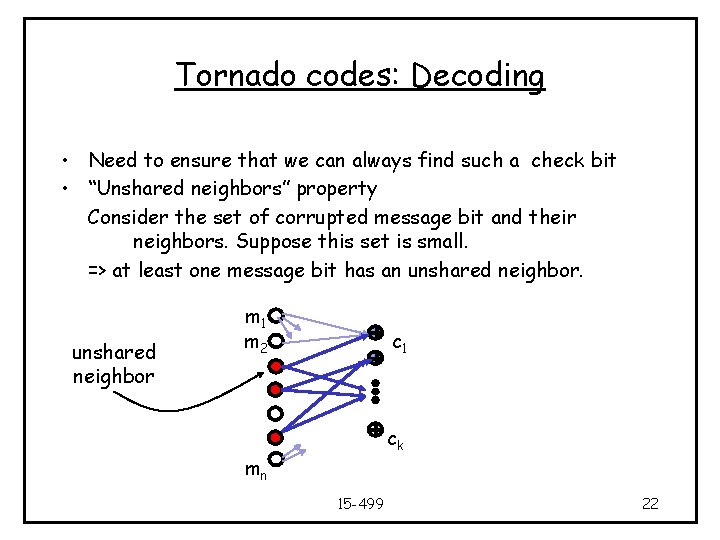
Tornado codes: Decoding • Need to ensure that we can always find such a check bit • “Unshared neighbors” property Consider the set of corrupted message bit and their neighbors. Suppose this set is small. => at least one message bit has an unshared neighbor m 1 m 2 c 1 ck mn 15 -499 22

Tornado codes: Decoding • Can we always find unshared neighbors? • Expander graphs give us this property • Also, [Luby et al] show that if we construct the graph from a specific kind of degree sequence, then we can always find unshared neighbors. 15 -499 23

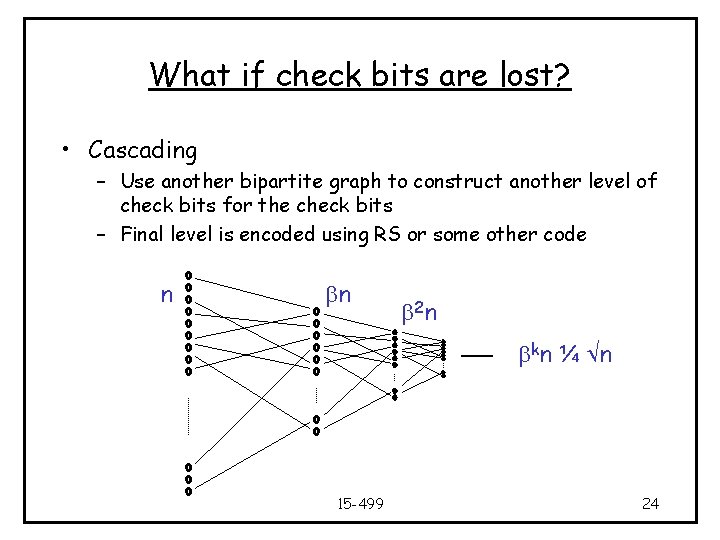
What if check bits are lost? • Cascading – Use another bipartite graph to construct another level of check bits for the check bits – Final level is encoded using RS or some other code n bn b 2 n bkn ¼ n 15 -499 24

Cascading • Total length of the code = n+bn+b 2 n+… · n/(1 -b) • Thus, rate is (1 -b) • Encoding time – for the first k stages : |E| = d x |V| = O(n) – for the last stage: n x n = O(n) • Decoding time – start from the last stage and move left – again proportional to |E| 15 -499 25

Outline ü Expander Graphs – Applications – Properties – Constructions ü Tornado Codes – Encoding/Decoding Algorithms – Brief Analysis • Expander Codes – Construction – Brief Analysis 15 -499 26

Expander Codes • Input: Regular expander G on n nodes, degree d Code C of block length d, rate r, rel. distance d • Output: Code C(G, C) of block length dn/2, rate 2 r-1, rel. distance ¼ d 2 • Linear time encoding/decoding 15 -499 27

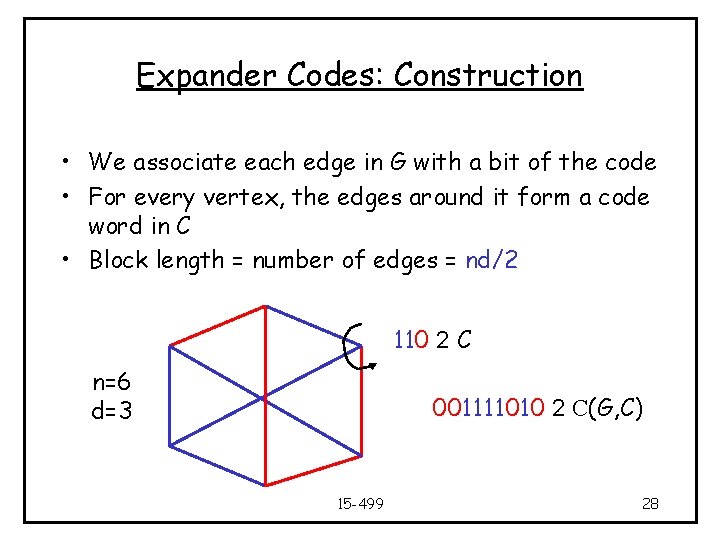
Expander Codes: Construction • We associate each edge in G with a bit of the code • For every vertex, the edges around it form a code word in C • Block length = number of edges = nd/2 110 2 C n=6 d=3 001111010 2 C(G, C) 15 -499 28

Expander Codes: Construction • Linear code C has rate r => there are (1 -r)d linear constraints on its bits (these constraints define a linear subspace of dimension rd) • Total number of constraints in the entire graph G = (1 -r) nd • Total length of code = nd/2 • => Total number of message bits = nd (r-1/2) • Therefore, rate is 2 (r-1/2) = 2 r-1 15 -499 29

Expander Codes: Construction • For linear codes, the minimum distance between two code words = minimum weight of a code word • Intuition: If the weight of a code word is small, then the weight of edges around some vertex is small => distance of C is small => contradiction 15 -499 30

Expander Graphs: Construction • Expander graphs: Any set of an nodes must have at most m = (a 2 + (a-a 2) l/d) dn/2 edges • So, a group of m edges must touch at least an vertices • One of these vertices touches at most m/2 an edges • But these should be at least dd for the code to be valid • So, (a + (1 -a) l/d) d > dd => a > (d - l/d)/(1 -l/d) • Minimum distance is atleast a (a + (1 -a) l/d) ¼ d 2 15 -499 31