10 2 Vectors and Vector Value Functions Quantities




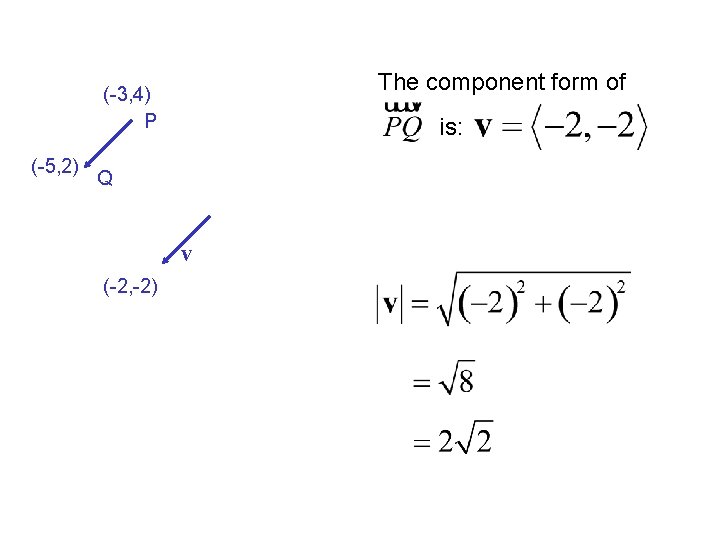



















- Slides: 30

10. 2 Vectors and Vector Value Functions

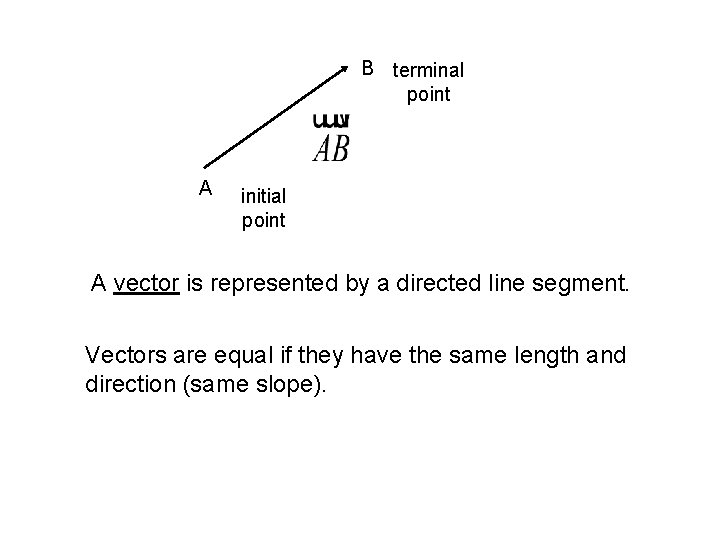
Quantities that we measure that have magnitude but not direction are called scalars. Quantities such as force, displacement or velocity that have direction as well as magnitude are represented by directed line segments. B terminal point A initial point The length is

B terminal point A initial point A vector is represented by a directed line segment. Vectors are equal if they have the same length and direction (same slope).

A vector is in standard position if the initial point is at the origin. y x The component form of this vector is:

y A vector is in standard position if the initial point is at the origin. x The component form of this vector is: The magnitude (length) of is:
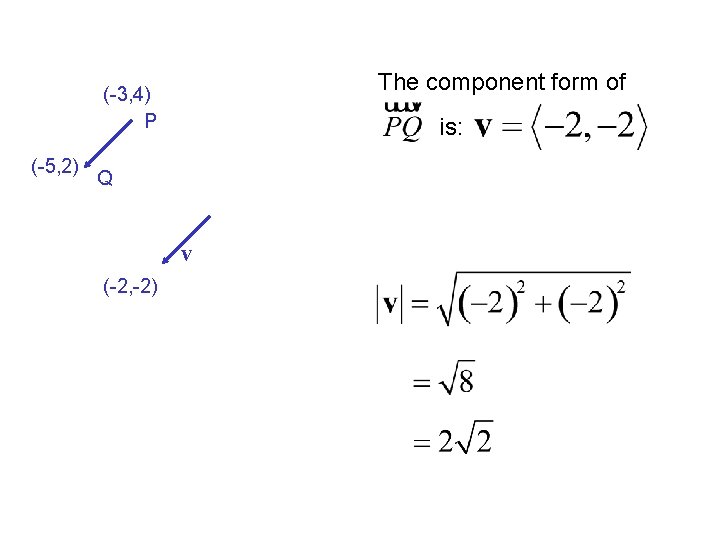
The component form of (-3, 4) P (-5, 2) is: Q v (-2, -2)

If Then v is a unit vector. is the zero vector and has no direction.

Vector Operations: (Add the components. ) (Subtract the components. )

Vector Operations: Scalar Multiplication: Negative (opposite):

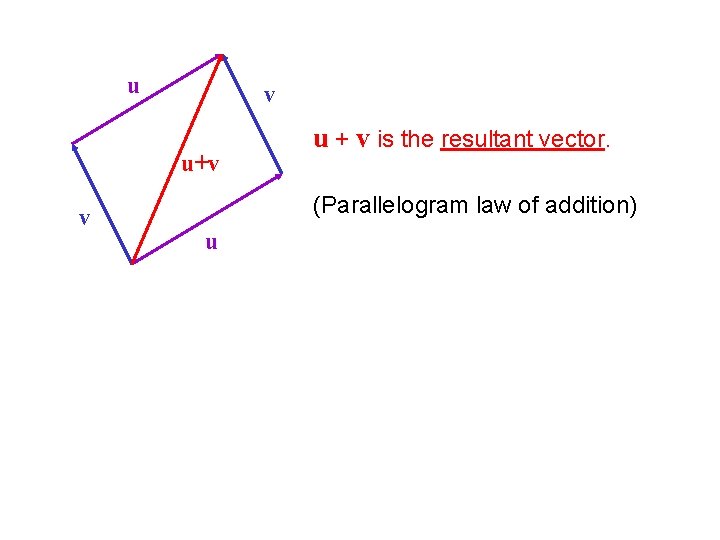
u v u+v v u + v is the resultant vector. (Parallelogram law of addition) u

The dot product (also called inner product) is defined as: Read “u dot v” Example:

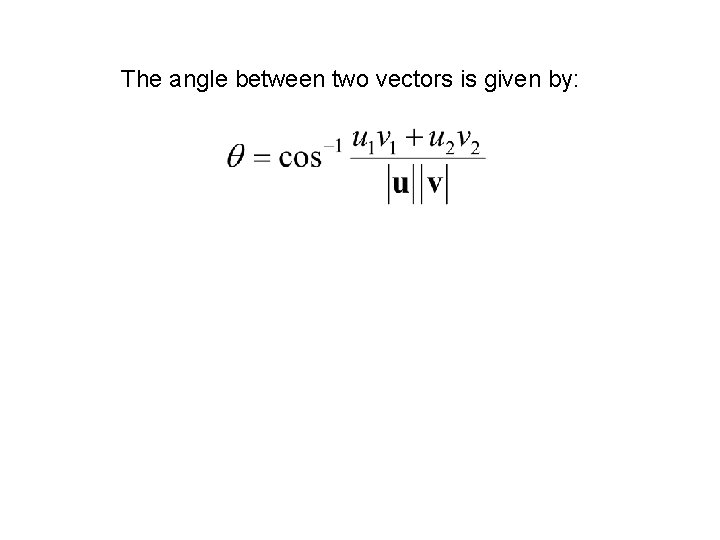
The angle between two vectors is given by:

The dot product (also called inner product) is defined as: This could be substituted in the formula for the angle between vectors (or solved for theta) to give:

Example: Find the angle between vectors u and v:

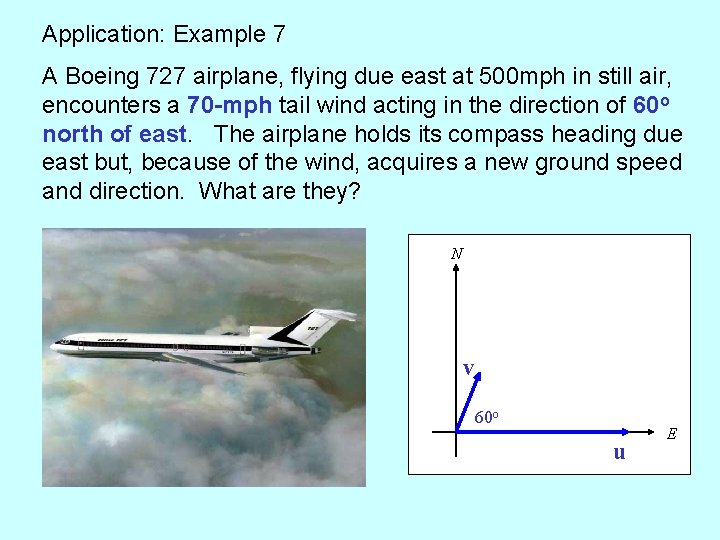
Application: Example 7 A Boeing 727 airplane, flying due east at 500 mph in still air, encounters a 70 -mph tail wind acting in the direction of 60 o north of east. The airplane holds its compass heading due east but, because of the wind, acquires a new ground speed and direction. What are they? N E

Application Example A Boeing 727 airplane, flying due east at 500 mph in still air, encounters a 70 -mph tail wind acting in the direction of 60 o north of east. The airplane holds its compass heading due east but, because of the wind, acquires a new ground speed and direction. What are they? N u E

Application: Example 7 A Boeing 727 airplane, flying due east at 500 mph in still air, encounters a 70 -mph tail wind acting in the direction of 60 o north of east. The airplane holds its compass heading due east but, because of the wind, acquires a new ground speed and direction. What are they? N v 60 o u E

Application: Example 7 A Boeing 727 airplane, flying due east at 500 mph in still air, encounters a 70 -mph tail wind acting in the direction of 60 o north of east. The airplane holds its compass heading due east but, because of the wind, acquires a new ground speed and direction. What are they? N We need to find the magnitude and direction of the resultant vector u + v. v u+v u E

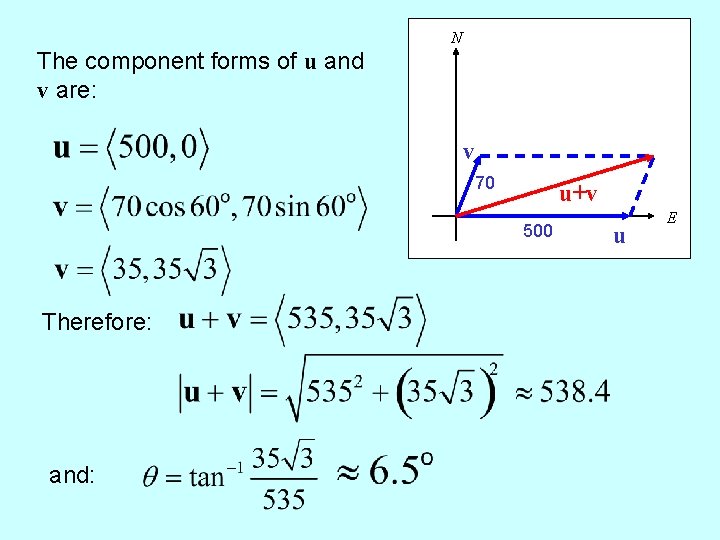
N The component forms of u and v are: v 70 u+v 500 Therefore: and: u E

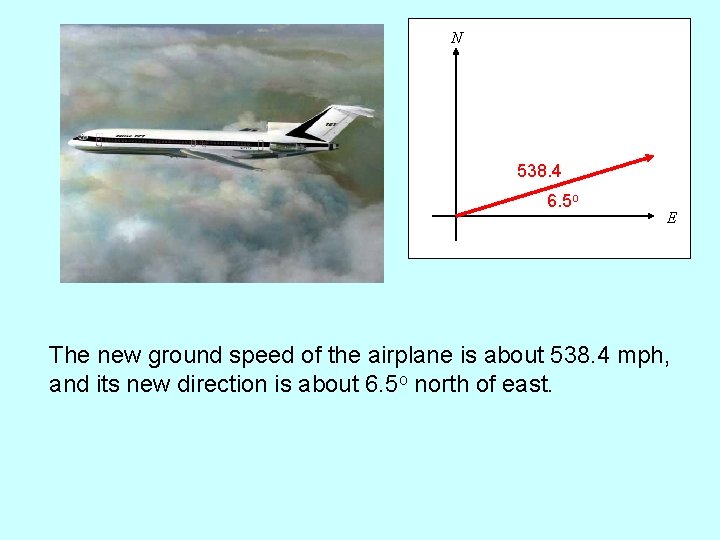
N 538. 4 6. 5 o E The new ground speed of the airplane is about 538. 4 mph, and its new direction is about 6. 5 o north of east.

We can describe the position of a moving particle by a vector, r(t) (position vector). If we separate r(t) into horizontal and vertical components, we can express r(t) as a linear combination of standard unit vectors i <1, 0> and j <0, 1>.

In three dimensions the component form becomes:

Most of the rules for the calculus of vectors are the same :

The exceptions? ? ? :

Example 7: A particle moves in an elliptical path so that its position at any time t ≥ 0 is given by <4 sin t, 2 cos t>. a. ) Find the velocity and acceleration vectors.

Example 7: A particle moves in an elliptical path so that its position at any time t ≥ 0 is given by <4 sin t, 2 cos t>. b. ) Find the velocity, acceleration, speed, and direction of motion at t = /4

Example 7: A particle moves in an elliptical path so that its position at any time t ≥ 0 is given by <4 sin t, 2 cos t>. c. ) Sketch the path of the particle and show the velocity vector at the point (4, 0). Graph parametrically x = 4 sin t y = 2 cos t At (4, 0): 4 = 4 sin t 1 = sin t and 0 = 2 cos t 0 = cos t v(t) = <4 cos t, -2 sin t> = <0, -2>

Example 7: A particle moves in an elliptical path so that its position at any time t ≥ 0 is given by <4 sin t, 2 cos t>. d. ) Does the particle travel clockwise or counterclockwise around the origin? The vector shows the particle travels clockwise around the origin.

Example : a) Write the equation of the tangent where At position: tangent: : slope: .

Example 6: b) Find the coordinates of each point on the path where the horizontal component of the velocity is 0. The horizontal component of the velocity is .
 Angular acceleration vs linear acceleration
Angular acceleration vs linear acceleration Magnitude of a vector
Magnitude of a vector Physical quantities of vectors
Physical quantities of vectors Units physical quantities and measurements
Units physical quantities and measurements Physical quantities and vectors
Physical quantities and vectors Examples of scalar quantities
Examples of scalar quantities Scalar and vector quantities
Scalar and vector quantities Why speed is a scalar quantity
Why speed is a scalar quantity Characteristics of vector quantity
Characteristics of vector quantity Time scalar or vector
Time scalar or vector Which of the following is a pair of vector quantities
Which of the following is a pair of vector quantities 30 examples of vector quantities
30 examples of vector quantities Vector versus scalar
Vector versus scalar Matlab vector of vectors
Matlab vector of vectors Initialize vector matlab
Initialize vector matlab Apa itu value creation
Apa itu value creation Piecewise functions absolute value
Piecewise functions absolute value Partitioning a line segment formula
Partitioning a line segment formula Vector unitario formula
Vector unitario formula How is vector resolution the opposite of vector addition
How is vector resolution the opposite of vector addition Position vector definition class 11
Position vector definition class 11 Eigen value and eigen vector
Eigen value and eigen vector Eigenvalue
Eigenvalue Eigen value and eigen vector
Eigen value and eigen vector Eigen value and eigen vector
Eigen value and eigen vector Vector function and space curves
Vector function and space curves Eigen value eigen vector
Eigen value eigen vector Big ed mona multimodal text
Big ed mona multimodal text In the previous lesson i learned that accounting
In the previous lesson i learned that accounting P-value and t-value
P-value and t-value D value and z value
D value and z value