RUANG EIGEN EIGEN VALUE and EIGEN VECTOR DIAGONALIZATION

RUANG EIGEN • EIGEN VALUE and EIGEN VECTOR • DIAGONALIZATION

NILAI EIGEN DAN VEKTOR EIGEN Definisi Jika A adalah matrks nxn, maka vektor tak nol x di Rn disebut vektor eigen dari A dan skalar disebut nilai eigen dari A jika terpenuhi persamaan Ax = x Menemukan nilai eigen A Untuk menemukan nilai eigen dari matriks A nxn, tuliskan Ax = x menjadi Ax = Ix atau ( I -A)x=0 Harus terdapat solusi tak-nol dari ( I -A)x=0. sistem persamaan tersebut memiliki solusi tak-nol jika det( I -A)=0 11/26/2020 Persamaan karakteristik Eigen Space 2

EIGEN VALUE and EIGEN VECTOR Contoh Temukan nilai eigen dari Solusi Persamaan karakteristik det( I -A)=0 =( -2) ( ( -3)+2) =( -2) ( -1) = 0 11/26/2020 Eigen Space Nilai eigen : 1, dan 2 3

EIGEN VALUE and EIGEN VECTOR Menemukan vektor eigen dari A Untuk tiap nilai eigen, kita dapat menemukan vektor eigen dari A dengan mensubtitusi nilai eigen ke sistem persamaan ( I -A)x=0 dan selesaikan persamaan tersebut. Ruang solusi persamaan tersebut disebut ruang eigen yang berpadanan dengan . Vektor-vektor eigen yang berpadanan dengan adalah vektor-vektor tak nol dalam ruang eigen Contoh Temukan basis bagi ruang eigen dari Solusi Nilai eigen dari A adalah 1 dan 2 (lihat halaman 3) 11/26/2020 Eigen Space 4

EIGEN VALUE and EIGEN VECTOR Solusi (lanjutan) Dengan mensubtitusi =1 ke persamaan: ( I-A) x = 0, didapat =1 ( I-A) x = 0 Basis bagi ruang eigen yang berpadanan dengan =1 adalah 11/26/2020 Eigen Space 5

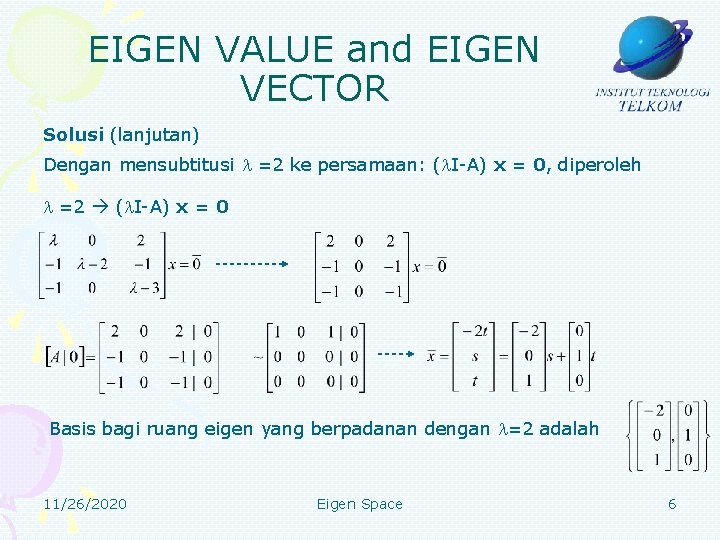
EIGEN VALUE and EIGEN VECTOR Solusi (lanjutan) Dengan mensubtitusi =2 ke persamaan: ( I-A) x = 0, diperoleh =2 ( I-A) x = 0 Basis bagi ruang eigen yang berpadanan dengan =2 adalah 11/26/2020 Eigen Space 6

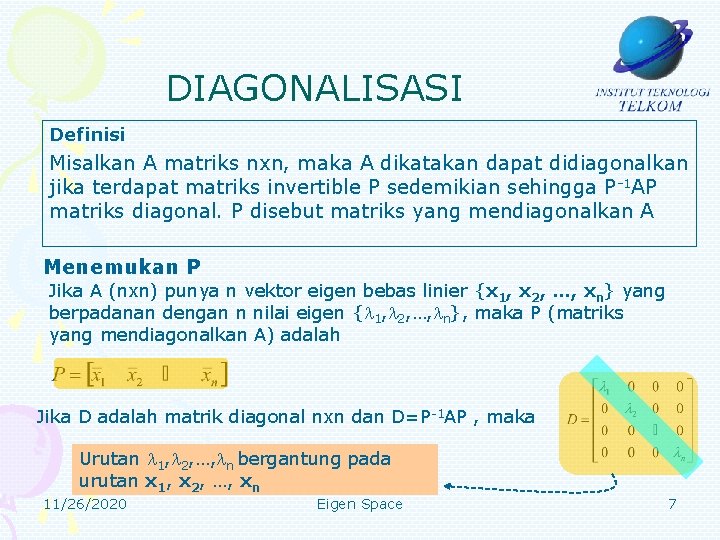
DIAGONALISASI Definisi Misalkan A matriks nxn, maka A dikatakan dapat didiagonalkan jika terdapat matriks invertible P sedemikian sehingga P-1 AP matriks diagonal. P disebut matriks yang mendiagonalkan A Menemukan P Jika A (nxn) punya n vektor eigen bebas linier {x 1, x 2, …, xn} yang berpadanan dengan n nilai eigen { 1, 2, …, n}, maka P (matriks yang mendiagonalkan A) adalah Jika D adalah matrik diagonal nxn dan D=P-1 AP , maka Urutan 1, 2, …, n bergantung pada urutan x 1, x 2, …, xn 11/26/2020 Eigen Space 7

DIAGONALISASI CONTOH temukan P (matriks yang mendiagonalkan A) dan D (D=P-1 AP) Solusi Basis bagi riuang eigen yang berpadanan dengan =1 (lihat hal 5) Basis bagi ruang eigen yg berpadanan dgn =2 (lihat hal 6) Maka, basis bagi ruang eigan dari A adalah n=3 (A 3 x 3) Bebas linier dan 11/26/2020 Eigen Space 8

Latihan 1. Misalkan Ax = kx , x adalah vektor taknol dan k : skalar taknol, temukan k dan x yang berpadanan dengan k jika 2. Temukan matriks C yang mendiagonalkan B dan matriks diagonal D dimana D=C-1 BC dengan 3. Misalkan A adalah matriks nxn mempunyai basis bebas linier dari ruang eigen yaitu: berpadanan dengan nilai eigen {1, 1, 5}. Temukan A 11/26/2020 Eigen Space 9