NILAI EIGEN VEKTOR Lecture6 EIGEN Nilai Eigen Eigen

NILAI EIGEN & VEKTOR Lecture-6 EIGEN

Nilai Eigen (Eigen Value) Aplikasi matriks dalam bidang teknologi yang melibatkan osilasi dan getaran sering dinyatakan dalam persamaan: Dimana A (aij) adalah matriks bujur sangkar dan merupakan bilangan skalar

Nilai Eigen (Eigen Value) X = 0 merupakan penyelesaian yang bisa diterima untuk sembarang nilai, tetapi tak banyak manfaatnya Jika x ≠ 0, maka nilai disebut nilai eigen, nilai karakteristik atau akar laten dari matriks A. Sedangkan penyelesaian yang sesuai untuk persamaan A. x = x disebut vektor eigen atau vektor karakteristik A

Nilai Eigen (Eigen Value) Persamaan tersebut dapat dinyakan sebagai yaitu

Nilai Eigen (Eigen Value) Persamaan ini dapat disederhanakan sebagai menjadi atau …………. . Matriks identitas muncul karena matriks hanya bisa dikurangi dengan matriks lain

Nilai Eigen (Eigen Value) Karena , dan x≠ 0, maka ………. . Nilai tersebut dinamakan determinan karakteristik A dan persamaannya disebut persamaan karakteristik. Contoh: carilah nilai eigen matriks

Nilai Eigen (Eigen Value) yang artinya Determinan karakteristik: Persamaan karakteristik

Nilai Eigen (Eigen Value) Carilah nilai eigen dari matriks

Vektor Eigen (Eigen Vector) Setiap nilai eigen yang didapat akan memiliki penyelesaian x yang sesuai, yang disebut vektor eigen. Pada matriks, istilah vektor menyatakan suatu matriks baris atau kolom Contoh: perhatikan persaman dengan Persamaan karakteristiknya adalah ……….

Vektor Eigen (Eigen Vector) Persamaan karakteristiknya adalah ……….

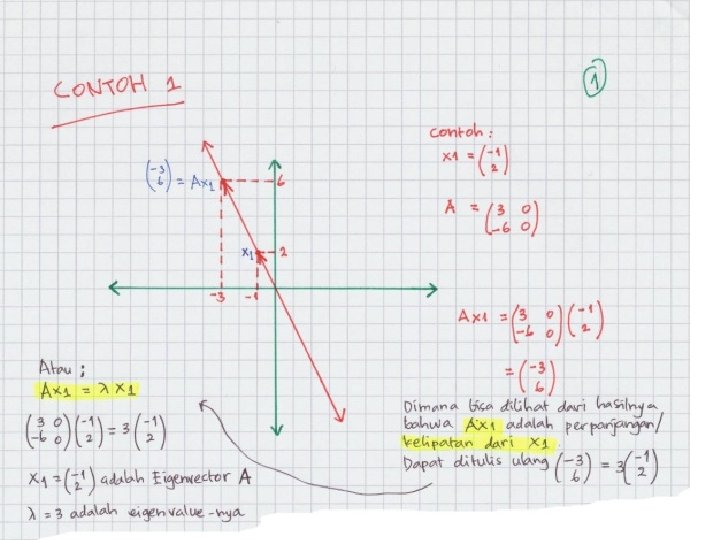
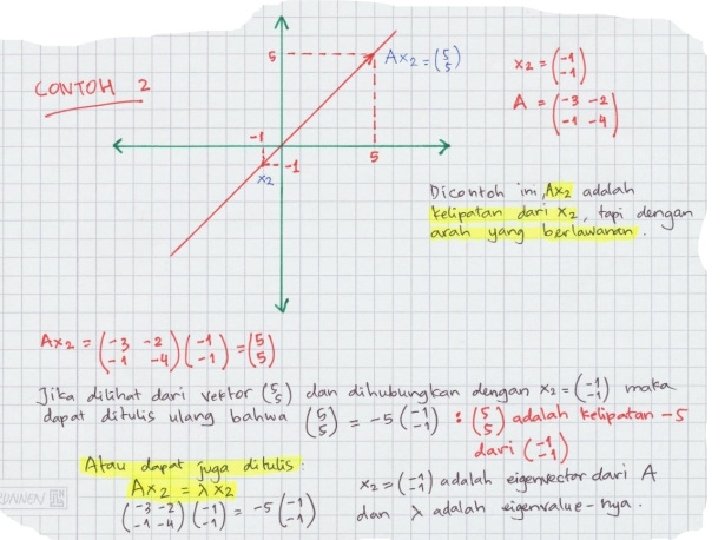
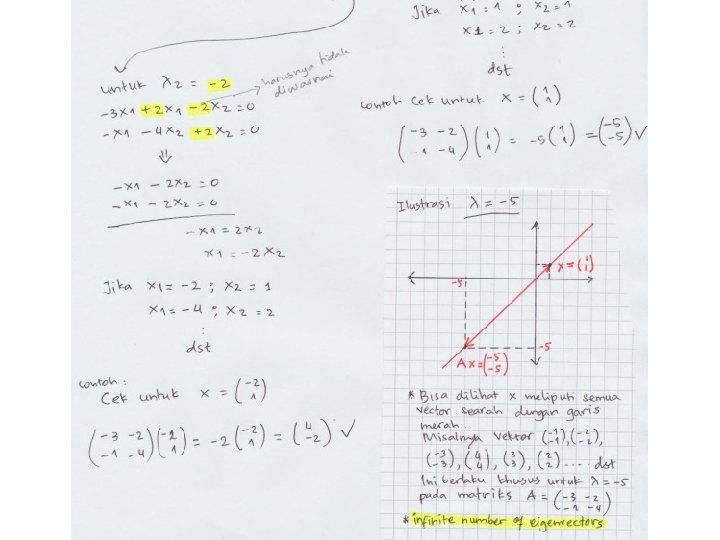
Vektor Eigen (Eigen Vector) Untuk , persamaan menjadi menghasilkan yang keduanya memberikan Hal itu menyatakan bahwa berapapun nilai x 1 , nilai x 2 akan selalu -3 kalinya.

Vektor Eigen (Eigen Vector) Sehingga bentuk umum vektor eigen dapat ditulis sebagai dan vektor eigen paling sederhana adalah Sedangkan untuk Sehingga bersesuaian dengan Dan dengan , vektor eigennya adalah …… merupakan vektor eigen yang bersesuain

Vektor Eigen (Eigen Vector) Tentukan nilai dan vektor eigen untuk persamaan dengan :