1 Trigonometric Functions Copyright 2013 2009 2005 Pearson



































- Slides: 38

1 Trigonometric Functions Copyright © 2013, 2009, 2005 Pearson Education, Inc. 1

1 Trigonometric Functions 1. 1 Angles 1. 2 Angle Relationships and Similar Triangles 1. 3 Trigonometric Functions 1. 4 Using the Definitions of the Trigonometric Functions Copyright © 2013, 2009, 2005 Pearson Education, Inc. 2

1. 1 Angles Basic Terminology ▪ Degree Measure ▪ Standard Position ▪ Coterminal Angles Copyright © 2013, 2009, 2005 Pearson Education, Inc. 3

1. 1 Example 1 Finding the Complement and the Supplement of an Angle (page 3) For an angle measuring 55°, find the measure of its complement and its supplement. Complement: 90° − 55° = 35° Supplement: 180° − 55° = 125° Copyright © 2013, 2009, 2005 Pearson Education, Inc. 4

1. 1 Example 2(a) Finding Measures of Complementary and Supplementary Angles (page 3) Find the measure of each angle. The two angles form a right angle, so they are complements. The measures of the two angles are and Copyright © 2013, 2009, 2005 Pearson Education, Inc. 5

1. 1 Example 2(b) Finding Measures of Complementary and Supplementary Angles (page 3) Find the measure of each angle. The two angles form a straight angle, so they are supplements. The measures of the two angles are and Copyright © 2013, 2009, 2005 Pearson Education, Inc. 6

1. 1 Example 3 Calculating with Degrees, Minutes, and Seconds (page 4) Perform each calculation. (a) (b) Copyright © 2013, 2009, 2005 Pearson Education, Inc. 7

1. 1 Example 4 Converting Between Decimal Degrees and Degrees, Minutes, and Seconds (page 5) (a) Convert 105° 20′ 32″ to decimal degrees. (b) Convert 85. 263° to degrees, minutes, and seconds. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 8

1. 1 Example 5 Finding Measures of Coterminal Angles (page 6) Find the angles of least possible positive measure coterminal with each angle. (a) 1106° Add or subtract 360° as many times as needed to obtain an angle with measure greater than 0° but less than 360°. An angle of 1106° is coterminal with an angle of 26°. (b) – 150° An angle of – 150° is coterminal with an angle of 210°. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 9

1. 1 Example 5 Finding Measures of Coterminal Angles (cont. ) (c) – 603° An angle of – 603° is coterminal with an angle of 117°. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 10

1. 1 Example 6 Analyzing the Revolutions of a CD Player (page 7) A wheel makes 270 revolutions per minute. Through how many degrees will a point on the edge of the wheel move in 5 sec? The wheel makes 270 revolutions in one minute or revolutions per second. In five seconds, the wheel makes revolutions. Each revolution is 360°, so a point on the edge of the wheel will move Copyright © 2013, 2009, 2005 Pearson Education, Inc. 11

1. 2 Angles Geometric Properties ▪ Triangles Copyright © 2013, 2009, 2005 Pearson Education, Inc. 12

1. 2 Example 1 Finding Angle Measures (page 11) Find the measures of angles 1, 2, 3, and 4 in the figure, given that lines m and n are parallel. Angles 2 and 3 are interior angles on the same side of the transversal, so they are supplements. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 13

1. 2 Example 1 Finding Angle Measures (cont. ) Angles 1 and 2 have equal measure because they are vertical angles, and angles 1 and 4 have equal measure because they are alternate exterior angles. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 14

1. 2 Example 2 Finding Angle Measures (page 12) The measures of two of the angles of a triangle are 33° and 26°. Find the measure of the third angle. The sum of the measures of the angles of a triangle is 360°. Let x = the measure of the third angle. The third angle measures 121°. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 15

1. 2 Example 3 Finding Angle Measures in Similar Triangles (page 13) In the figure, triangles DEF and GHI are similar. Find the measures of angles G and I. The triangles are similar, so the corresponding angles have the same measure. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 16

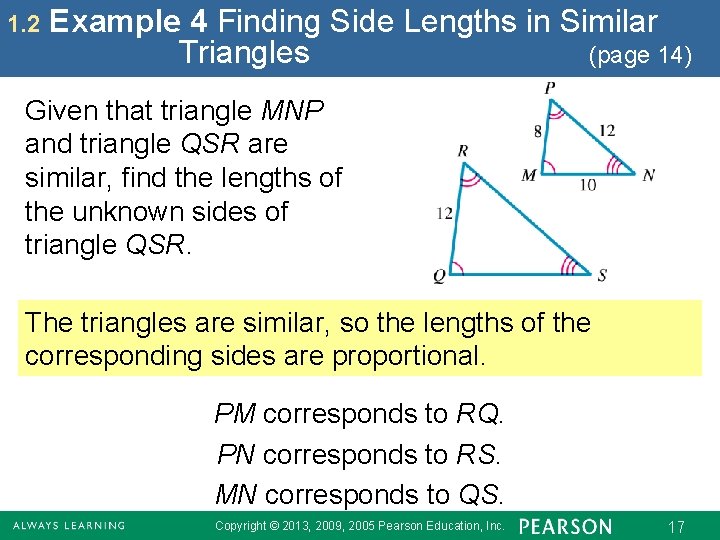
1. 2 Example 4 Finding Side Lengths in Similar Triangles (page 14) Given that triangle MNP and triangle QSR are similar, find the lengths of the unknown sides of triangle QSR. The triangles are similar, so the lengths of the corresponding sides are proportional. PM corresponds to RQ. PN corresponds to RS. MN corresponds to QS. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 17

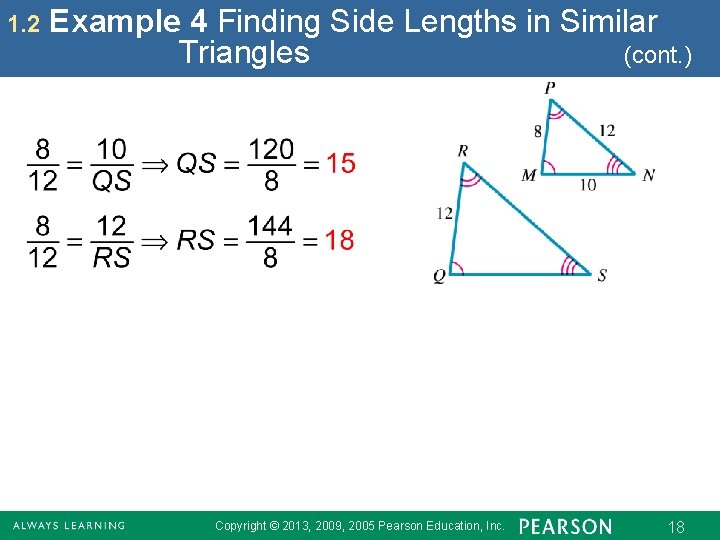
1. 2 Example 4 Finding Side Lengths in Similar Triangles (cont. ) Copyright © 2013, 2009, 2005 Pearson Education, Inc. 18

1. 2 Example 5 Finding the Height of a Flagpole (page 14) Joey wants to know the height of a tree in a park near his home. The tree casts a 38 -ft shadow at the same time that Joey, who is 63 in. tall, casts a 42 -in. shadow. Find the height of the tree. Let x = the height of the tree The tree is 57 feet tall. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 19

1. 3 Trigonometric Functions ▪ Quadrantal Angles Copyright © 2013, 2009, 2005 Pearson Education, Inc. 20

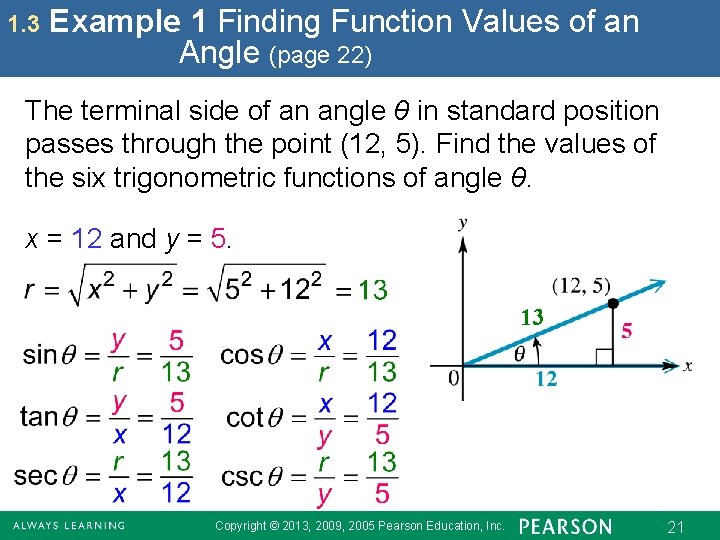
1. 3 Example 1 Finding Function Values of an Angle (page 22) The terminal side of an angle θ in standard position passes through the point (12, 5). Find the values of the six trigonometric functions of angle θ. x = 12 and y = 5. 13 Copyright © 2013, 2009, 2005 Pearson Education, Inc. 21

1. 3 Example 2 Finding Function Values of an Angle (page 22) The terminal side of an angle θ in standard position passes through the point (8, – 6). Find the values of the six trigonometric functions of angle θ. x = 8 and y = – 6. 10 Copyright © 2013, 2009, 2005 Pearson Education, Inc. 6 22

1. 3 Example 2 Finding Function Values of an Angle (cont. ) Copyright © 2013, 2009, 2005 Pearson Education, Inc. 23

1. 3 Example 3 Finding Function Values of an Angle (page 23) Find the values of the six trigonometric functions of angle θ in standard position, if the terminal side of θ is defined by 3 x – 2 y = 0, x ≤ 0. Since x ≤ 0, the graph of the line 3 x – 2 y = 0 is shown to the left of the y-axis. Find a point on the line: Let x = – 2. Then A point on the line is (– 2, – 3). Copyright © 2013, 2009, 2005 Pearson Education, Inc. 24

1. 3 Example 3 Finding Function Values of an Angle (cont. ) Copyright © 2013, 2009, 2005 Pearson Education, Inc. 25

1. 3 Example 4(a) Finding Function Values of Quadrantal Angles (page 25) Find the values of the six trigonometric functions of a 360° angle. The terminal side passes through (2, 0). So x = 2 and y = 0 and r = 2. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 26

1. 3 Example 4(b) Finding Function Values of Quadrantal Angles (page 25) Find the values of the six trigonometric functions of an angle θ in standard position with terminal side through (0, – 5). x = 0 and y = – 5 and r = 5. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 27

1. 4 Using the Definitions of the Trigonometric Functions Reciprocal Identities ▪ Signs and Ranges of Function Values ▪ Pythagorean Identities ▪ Quotient Identities Copyright © 2013, 2009, 2005 Pearson Education, Inc. 28

1. 4 Example 1 Using the Reciprocal Identities (page 29) Find each function value. (a) tan θ, given that cot θ = 4. tan θ is the reciprocal of cot θ. (b) sec θ, given that sec θ is the reciprocal of cos θ. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 29

1. 4 Example 2 Finding Function Values of an Angle (page 30) Determine the signs of the trigonometric functions of an angle in standard position with the given measure. (a) 54° (b) 260° (c) – 60° (a) A 54º angle in standard position lies in quadrant I, so all its trigonometric functions are positive. (b) A 260º angle in standard position lies in quadrant III, so its sine, cosine, secant, and cosecant are negative, while its tangent and cotangent are positive. (c) A – 60º angle in standard position lies in quadrant IV, so cosine and secant are positive, while its sine, cosecant, tangent, and cotangent are negative. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 30

1. 4 Example 3 Identifying the Quadrant of an Angle (page 31) Identify the quadrant (or possible quadrants) of an angle θ that satisfies the given conditions. (a) tan θ > 0, csc θ < 0 tan θ > 0 in quadrants I and III, while csc θ < 0 in quadrants III and IV. Both conditions are met only in quadrant III. (b) sin θ > 0, csc θ > 0 sin θ > 0 in quadrants I and II, as is csc θ. Both conditions are met in quadrants I and II. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 31

1. 4 Example 4 Deciding Whether a Value is in the Range of a Trigonometric Function (page 32) Decide whether each statement is possible or impossible. (a) cot θ = – 0. 999 (b)cos θ = – 1. 7 (c)csc θ = 0 (a) cot θ = – 0. 999 is possible because the range of cot θ is (b) cos θ = – 1. 7 is impossible because the range of cos θ is [– 1, 1]. (c) csc θ = 0 is impossible because the range of csc θ is Copyright © 2013, 2009, 2005 Pearson Education, Inc. 32

1. 4 Example 5 Finding All Function Values Given One Value and the Quadrant (page 32) Angle θ lies in quadrant III, and Find the values of the other five trigonometric functions. Since and y = – 8. and θ lies in quadrant III, then x = – 5 Copyright © 2013, 2009, 2005 Pearson Education, Inc. 33

1. 4 Example 5 Finding All Function Values Given One Value and the Quadrant (cont. ) Copyright © 2013, 2009, 2005 Pearson Education, Inc. 34

1. 4 Example 6 Finding Other Function Values Given One Value and the Quadrant (page 34) Find cos θ and tan θ given that sin θ cos θ > 0. and Reject the negative root. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 35

1. 4 Example 6 Finding Other Function Values Given One Value and the Quadrant (cont. ) Copyright © 2013, 2009, 2005 Pearson Education, Inc. 36

1. 4 Example 7 Using Identities to Find Function Values (page 35) Find sin θ and cos θ given that cot θ θ is in quadrant II. and Since θ is in quadrant II, sin θ > 0 and cos θ < 0. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 37

1. 4 Example 7 Finding Other Function Values Given One Value and the Quadrant (cont. ) Copyright © 2013, 2009, 2005 Pearson Education, Inc. 38
 2009 pearson education inc
2009 pearson education inc Copyright 2009 pearson education inc
Copyright 2009 pearson education inc Copyright 2009 pearson education inc
Copyright 2009 pearson education inc Copyright 2009 pearson education inc
Copyright 2009 pearson education inc Copyright 2009 pearson education inc
Copyright 2009 pearson education inc Copyright 2009 pearson education inc
Copyright 2009 pearson education inc 2005 pearson prentice hall inc
2005 pearson prentice hall inc Plan nacional del buen vivir 2009 al 2013
Plan nacional del buen vivir 2009 al 2013 International color consortium
International color consortium Dell all rights reserved copyright 2009
Dell all rights reserved copyright 2009 Diffrazione della luce zanichelli
Diffrazione della luce zanichelli Copyright 2009
Copyright 2009 Copyright 2009
Copyright 2009 Copyright 2005
Copyright 2005 Copyright 2005
Copyright 2005 Copyright 2005
Copyright 2005 Copyright 2005
Copyright 2005 Copyright 2005
Copyright 2005 Copyright 2005
Copyright 2005 Copyright 2005
Copyright 2005 Copyright 2005
Copyright 2005 Copyright 2005
Copyright 2005 2009 pearson education inc
2009 pearson education inc 2009 pearson education inc
2009 pearson education inc 2009 pearson education inc
2009 pearson education inc Pearson 2009
Pearson 2009 Pearson 2009
Pearson 2009 Pearson 2009
Pearson 2009 Pearson education 2009
Pearson education 2009 2009 pearson education inc
2009 pearson education inc 2009 pearson education inc
2009 pearson education inc Mbti personal impact report
Mbti personal impact report Pearson education limited 2005
Pearson education limited 2005 2005 pearson prentice hall inc
2005 pearson prentice hall inc Pearson education limited 2005
Pearson education limited 2005 2013 pearson education inc
2013 pearson education inc 2013 pearson education inc
2013 pearson education inc 2013 pearson education inc
2013 pearson education inc 2013 pearson education inc
2013 pearson education inc






























































