5 Trigonometric Identities Copyright 2013 2009 2005 Pearson

5 Trigonometric Identities Copyright © 2013, 2009, 2005 Pearson Education, Inc. 1

5 Trigonometric Identities 5. 1 Fundamental Identities 5. 3 Sum and Difference Identities for Cosine 5. 4 Sum and Difference Identities for Sine and Tangent 5. 5 Double-Angle Identities 5. 6 Half-Angle Identities Copyright © 2013, 2009, 2005 Pearson Education, Inc. 2

5. 1 Trigonometric Identities Fundamental Identities ▪ Using the Fundamental Identities Copyright © 2013, 2009, 2005 Pearson Education, Inc. 3

5. 1 Example 1 Finding Trigonometric Function Values Given One Value and the Quadrant (page 191) If value. (a) and is in quadrant IV, find each function In quadrant IV, is negative. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 4

5. 1 Example 1 Finding Trigonometric Function Values Given One Value and the Quadrant (cont. ) If value. and is in quadrant IV, find each function (b) (c) Copyright © 2013, 2009, 2005 Pearson Education, Inc. 5

5. 1 Example 2 Expressing One Function in Terms of Another (page 192) Copyright © 2013, 2009, 2005 Pearson Education, Inc. 6

5. 1 Example 3 Rewriting an Expression in Terms of Sine and Cosine (page 193) Write in terms of and , and then simplify the expression so that no quotient appear. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 7

5. 3 Sum and Difference Identities for Cosine Difference Identity for Cosine ▪ Sum Identity for Cosine ▪ Cofunction Identities ▪ Applying the Sum and Difference Identities Copyright © 2013, 2009, 2005 Pearson Education, Inc. 8

5. 3 Example 1 Finding Exact Cosine Function Values (page 206) Find the exact value of each expression. (a) Copyright © 2008 Pearson Addison-Wesley. All rights reserved. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 9

5. 3 Example 1 Finding Exact Cosine Function Values (cont. ) (b) (c) Copyright © 2013, 2009, 2005 Pearson Education, Inc. 10

5. 3 Example 2 Using Cofunction Identities to Find θ (page 208) Find an angle θ that satisfies each of the following. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 11

5. 3 Example 3 Reducing cos (A – B) to a Function of a Single Variable (page 208) Write cos(90° + θ) as a trigonometric function of θ alone. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 12

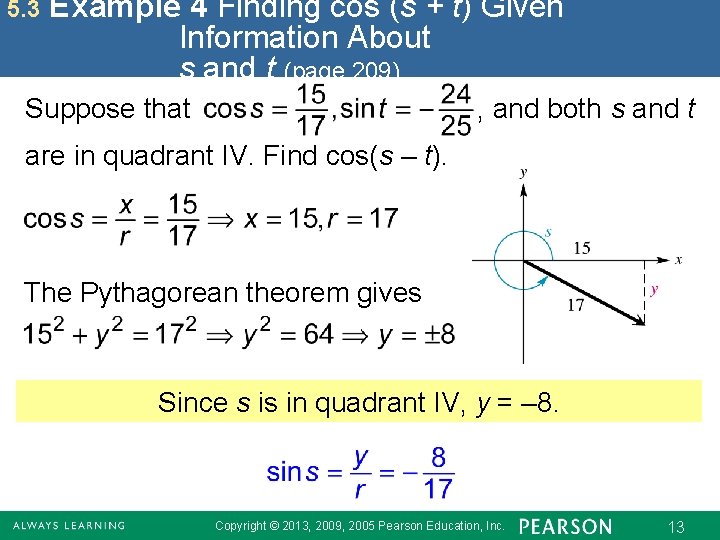
5. 3 Example 4 Finding cos (s + t) Given Information About s and t (page 209) Suppose that , and both s and t are in quadrant IV. Find cos(s – t). The Pythagorean theorem gives Since s is in quadrant IV, y = – 8. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 13

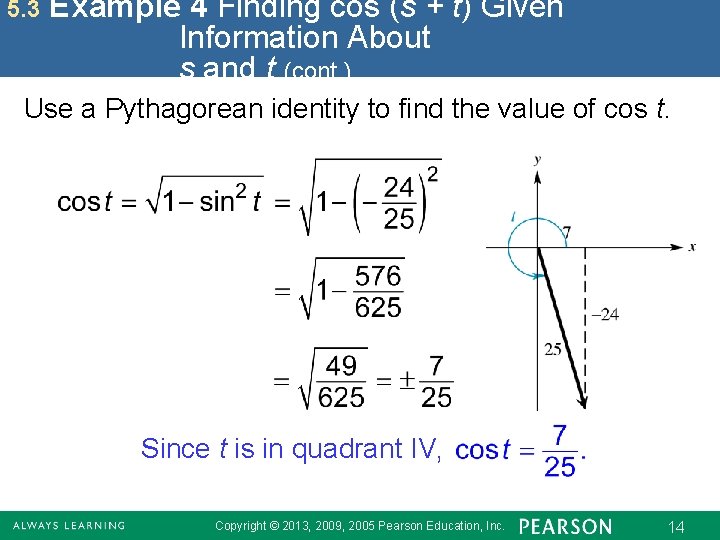
5. 3 Example 4 Finding cos (s + t) Given Information About s and t (cont. ) Use a Pythagorean identity to find the value of cos t. Since t is in quadrant IV, Copyright © 2013, 2009, 2005 Pearson Education, Inc. 14

5. 3 Example 4 Finding cos (s + t) Given Information About s and t (cont. ) Copyright © 2013, 2009, 2005 Pearson Education, Inc. 15

5. 3 Example 5 Applying the Cosine Difference Identity to Voltage (page 221) Because household current is supplied at different voltages in different countries, international travelers often carry electrical adapters to connect items they have brought from home to a power source. The voltage V in a typical European 220 -volt outlet can be expressed by the function (a) European generators rotate at precisely 50 cycles per second. Determine ω for these electric generators. Each cycle is radians at 50 cycles per second. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 16

5. 3 Example 5 Applying the Cosine Difference Identity to Voltage (cont. ) (b) What is the maximum voltage in the outlet? The maximum value of is 1. The maximum voltage in the outlet is Copyright © 2013, 2009, 2005 Pearson Education, Inc. 17

5. 3 Example 5 Applying the Cosine Difference Identity to Voltage (cont. ) (c) Determine the least positive value of that the graph of in radians so is the same as Using the sum identity for cosine gives Copyright © 2013, 2009, 2005 Pearson Education, Inc. 18

5. 4 Sum and Difference Identities for Sine and Tangent Sum and Difference Identities for Sine ▪ Sum and Difference Identities for Tangent ▪ Applying the Sum and Difference Identities Copyright © 2013, 2009, 2005 Pearson Education, Inc. 19

5. 4 Example 1 Finding Exact Sine and Tangent Function Values (page 217) Find the exact value of each expression. (a) Copyright © 2013, 2009, 2005 Pearson Education, Inc. 20

5. 4 Example 1 Finding Exact Sine and Tangent Function Values (cont. ) (b) Copyright © 2013, 2009, 2005 Pearson Education, Inc. 21

5. 4 Example 1 Finding Exact Sine and Tangent Function Values (cont. ) (c) Copyright © 2013, 2009, 2005 Pearson Education, Inc. 22

5. 4 Example 2 Writing Functions as Expressions Involving Functions of θ (page 218) Write each function as an expression involving functions of θ. (a) (b) (c) Copyright © 2013, 2009, 2005 Pearson Education, Inc. 23

5. 4 Example 3 Finding Function Values and the Quadrant of A – B (page 218) Suppose that A and B are angles in standard position with and Find each of the following. (c) the quadrant of A – B. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 24

5. 4 Example 3 Finding Function Values and the Quadrant of A – B (cont. ) The identity for sin(A – B) requires sin A, cos A, sin B, and cos B. The identity for tan(A – B) requires tan A and tan B. We must find sin A, tan A, cos B and tan B. Because A is in quadrant III, sin A is negative and tan A is positive. Because B is in quadrant IV, cos B is positive and tan B is negative. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 25

5. 4 Example 3(a) Finding Function Values and the Quadrant of A – B (cont. ) To find sin A and cos B, use the identity Copyright © 2013, 2009, 2005 Pearson Education, Inc. 26

5. 4 Example 3(b) Finding Function Values and the Quadrant of A – B (cont. ) To find tan A and tan B, use the identity Copyright © 2013, 2009, 2005 Pearson Education, Inc. 27

5. 4 Example 3(c) Finding Function Values and the Quadrant of A – B (cont. ) From parts (a) and (b), sin (A − B) < 0 and tan (A − B) < 0. The only quadrant in which the values of both the sine and the tangent are negative is quadrant IV, so (A − B) is in quadrant IV. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 28

5. 5 Double-Angle Identities ▪ An Application ▪ Product-to. Sum and Sum-to-Product Identities Copyright © 2013, 2009, 2005 Pearson Education, Inc. 29

5. 5 Example 1 Finding Function Values of 2θ Given Information About θ (page 225) The identity for sin 2θ requires cos θ. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 30

5. 5 Example 1 Finding Function Values of 2θ Given Information About θ (cont. ) Copyright © 2013, 2009, 2005 Pearson Education, Inc. 31

5. 5 Example 1 Finding Function Values of 2θ Given Information About θ (cont. ) Alternatively, find tan θ and then use the tangent double-angle identity. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 32

5. 5 Example 2 Finding Function Values of θ Given Information About 2θ (page 226) Find the values of the six trigonometric functions of θ if Use the identity to find sin θ: θ is in quadrant III, so sin θ is negative. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 33

5. 5 Example 2 Finding Function Values of θ Given Information About 2θ (cont. ) Use the identity to find cos θ: θ is in quadrant III, so cos θ is negative. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 34

5. 5 Example 2 Finding Function Values of θ Given Information About 2θ (cont. ) Copyright © 2013, 2009, 2005 Pearson Education, Inc. 35

5. 5 Example 4 Simplifying Expressions Using Double-Angle Identities (page 227) Simplify each expression. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 36

5. 5 Example 5 Deriving a Multiple-Angle Identity (page 228) Write cos 3 x in terms of cos x. Distributive property. Simplify. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 37

5. 6 Half-Angle Identities ▪ Applying the Half-Angle Identities Copyright © 2013, 2009, 2005 Pearson Education, Inc. 38

5. 6 Example 1 Using a Half-Angle Identity to Find an Exact Value (page 234) Find the exact value of sin 22. 5° using the half-angle identity for sine. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 39

5. 6 Example 2 Using a Half-Angle Identity to Find an Exact Value (page 234) Find the exact value of tan 75° using the identity Copyright © 2013, 2009, 2005 Pearson Education, Inc. 40

5. 6 Example 3 Finding Function Values of s 2 Given Information About s (page 234) The angle associated with lies in quadrant II since is positive while Copyright © 2013, 2009, 2005 Pearson Education, Inc. are negative. 41

5. 6 Example 3 Finding Function Values of s 2 Given Information About s (cont. ) Copyright © 2013, 2009, 2005 Pearson Education, Inc. 42

5. 6 Example 4 Simplifying Expressions Using the Half-Angle Identities (page 235) Simplify each expression. This matches part of the identity for . Substitute 8 x for A: Copyright © 2013, 2009, 2005 Pearson Education, Inc. 43