1 Repetisjon av sannsynlighetsregning Jrn Vatn NTNU 2

1 Repetisjon av sannsynlighetsregning Jørn Vatn NTNU

2 Tilfeldig forsøk • Mange situasjoner er kjennetegnet ved at vi ikke vet hva fremtiden vil bringe. Noen eksempler er gitt nedenfor – Vi setter en lyspære i drift, og registrerer tiden, T, det tar før den svikter. – Vi kaster en terning, og registrer hvor mange øyne terningkastet gir. – Vi bygger en grunnmur, og registrer tiden, T, det tar å ferdigstille grunnmuren. – Vi regisserer om et prosjekt fullføres innen kontraktsfestet tidspunkt.

3 Utfallsrom • Selv om vi på forhånd ikke vet resultatet av et tilfeldig forsøk, vil vi kunne si noe om mulige utfall av forsøket. • Dette kaller vi utfallsrommet. • Utfallsrommet betegnes S (fra engelsk: Sample space). – I eksemplet med lyspæra vil f eks utfallsrommet være den positive delen av den reelle tallinja. – For et terningkast er utfallsrommet S = {1, 2, 3, 4, 5, 6} – For eksemplet med grunnmuren er utfallsrommet positive reelle tall

4 Venndiagram • Venndiagram er hensiktsmessig når vi vil se på delmengder av utfallsrommet. • Vi tegner hele utfallsrommet som et rektangel, og så tegner vi de mengder vi vil betrakte som lukkede kurver, f eks en sirkel eller en ellipse

5 Hendelser • Sannsynlighet er definert for hendelser • En hendelse er som ordet tilsier noe som kan hende (inntreffe), på den andre siden kan det også hende at hendelsen ikke inntreffer – {Det regner i morgen} er derfor en hendelse, og – {Prosjektet når tidsfristen} er også en hendelse. – Begge disse hendelsene kan hende, men det kan også hende at de ikke inntreffer. • Det gir ikke mening å si at T = {levetiden til en gitt lyspære} er en hendelse • Derimot kan vi si at {levetiden til en gitt lyspære er mindre enn et år} er en hendelse

6 Megndelære • • Snitt Union Disjunkte mengder Komplementære mengder

7 Union • Unionen av to mengder A og B: • A B betegner de enkeltutfall som inngår i A eller B eller (A og B)

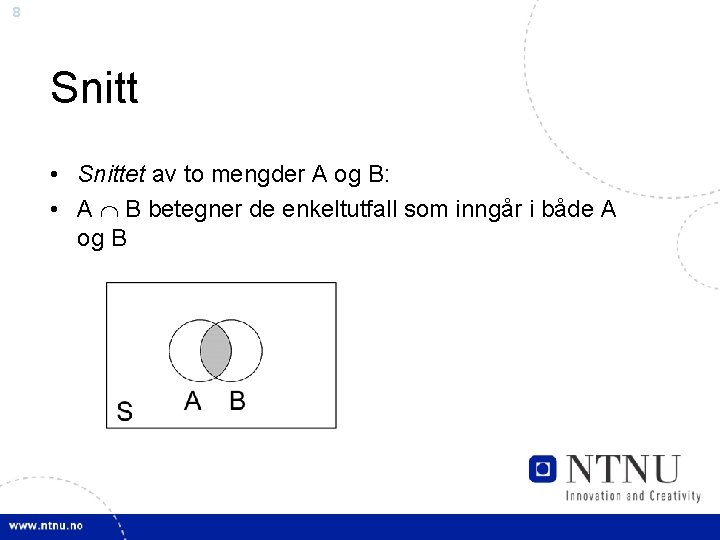
8 Snitt • Snittet av to mengder A og B: • A B betegner de enkeltutfall som inngår i både A og B

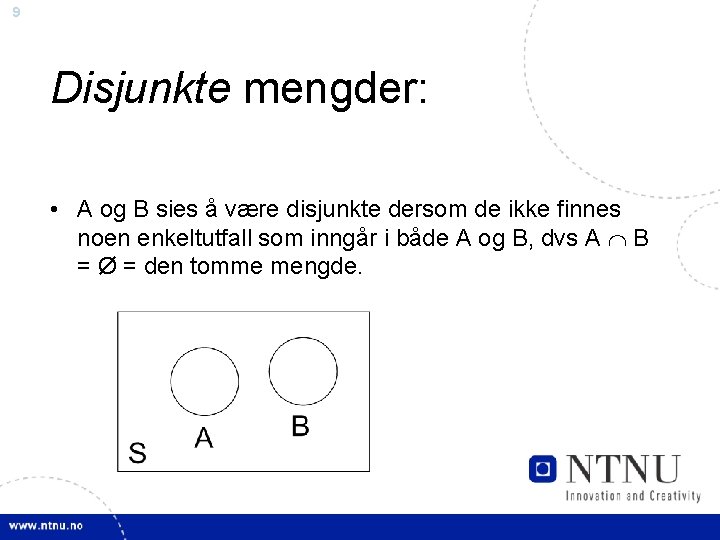
9 Disjunkte mengder: • A og B sies å være disjunkte dersom de ikke finnes noen enkeltutfall som inngår i både A og B, dvs A B = Ø = den tomme mengde.

10 Komplementærmengder • B sies å være komplementærmengden til A dersom B inneholder de enkeltutfall som ikke inngår i A • Vi skriver AC for å betegne komplementærmengden til A

11 Sannsynlighet • Sannsynlighet er en mengde-funksjon Pr( ) som knytter reelle tall til hendelser A 1, A 2, . . . i utfallsrommet S for et tilfeldig forsøk. • Funksjonen Pr( ) kan kun ta verdier i intervallet fra 0 til 1, dvs sannsynligheter må være større eller lik 0, og mindre eller lik 1 A 2 S 0 Pr(A 1) Pr(A 2) 1

12 Kolmogorovs grunnleggende aksiomer 1. 0 Pr(A) 2. Pr(S) = 1 3. Dersom A 1, A 2, . . . er en sekvens av disjunkte hendelser, skal Pr(A 1 A 2 . . . ) = Pr(A 1) + Pr(A 2) +. . .

13 Betinget sannsynlighet • I en del situasjoner vil sannsynligheten for en hendelse A endre seg dersom vi får ny informasjon om en relatert hendelse B. • I slike situasjoner innfører vi begrepet betinget sannsynlighet, og skriver • Pr(A|B) = Den betingete sannsynligheten for at A skal inntreffe gitt at hendelse B har inntruffet.

14 Uavhengige hendelser • A og B sies å være (stokastisk) uavhengig dersom informasjon om hvorvidt B er inntruffet ikke påvirker sannsynligheten for at A vil inntreffe, dvs • Pr(A|B) = Pr(A)

15 Basisregler for sannsynlighetsregning • • Pr(A B) = Pr(A) + Pr(B) - Pr(A B) = Pr(A) Pr(B) hvis A og B er uavhengig Pr(AC) = Pr(A ikke inntreffer) = 1 - Pr(A) Pr(A|B) = Pr(A B) / Pr(B)

16 Oppdeling av utfallsrommet • A 1, A 2, …, Ar sies å være en oppdeling av utfallsrommet dersom unionen av alle Ai-ene dekker utfallsrommet, dvs A 1 A 2 … Ar = S og Ai-ene er parvis disjunkte, dvs Ai Aj = Ø for i j

17 Loven om total sannsynlighet

18 Bayes formel • Dersom A 1, A 2, …, Ar representere en oppdeling av utfallsrommet S, og B er en vilkårlig hendelse i S kan vi beregne Pr(Aj|B) ved

19 Tilfeldig størrelser • En tilfeldig størrelse (stokastisk variabel), er en størrelse som vi ikke vet hvilken verdi vil ta, men – Vi kan uttrykke statistiske egenskaper til størrelsen, eller gi sannsynlighetsutsagn om den • Hendelser kan inntreffe, evt ikke inntreffe (“sort/hvit”), en tilfeldig størrelse er relatert til verdi, den kan ta ulike verdier (“farger”) • Vi benytter sannsynligheter til å beskrive sannsynligheten for at den tilfeldige størrelsen kan ta ulike verdier – Kumulativ fordelingsfunksjon (S-kurve, cumulative distribution function) – Sannsynlighetstetthet (histogram, probability distribution function) • Eksempler på tilfeldige størrelser – Totale prosjektkostnader – Varighet til prosjektet (f eks i dager fra oppstart)

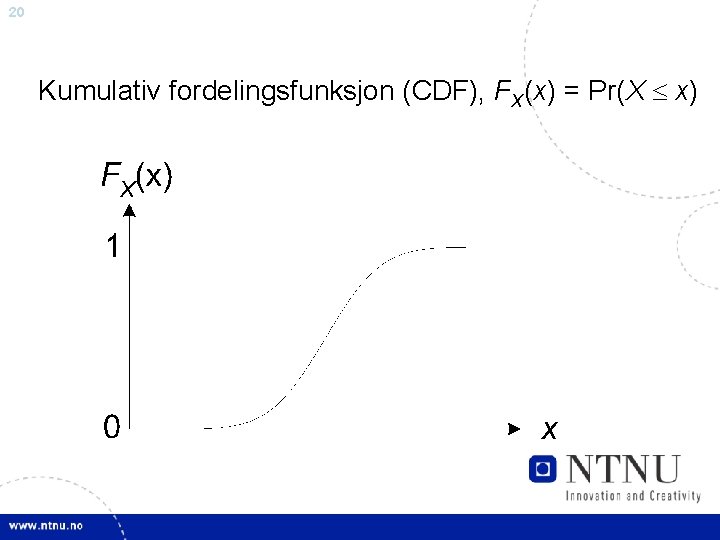
20 Kumulativ fordelingsfunksjon (CDF), FX(x) = Pr(X x)

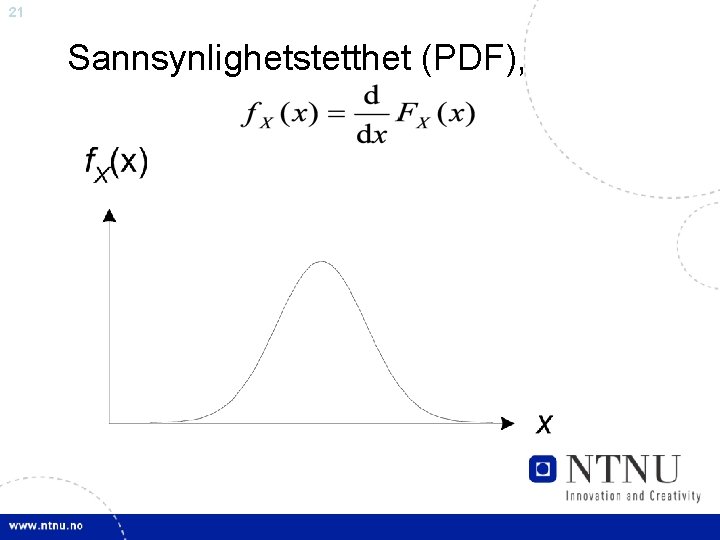
21 Sannsynlighetstetthet (PDF),

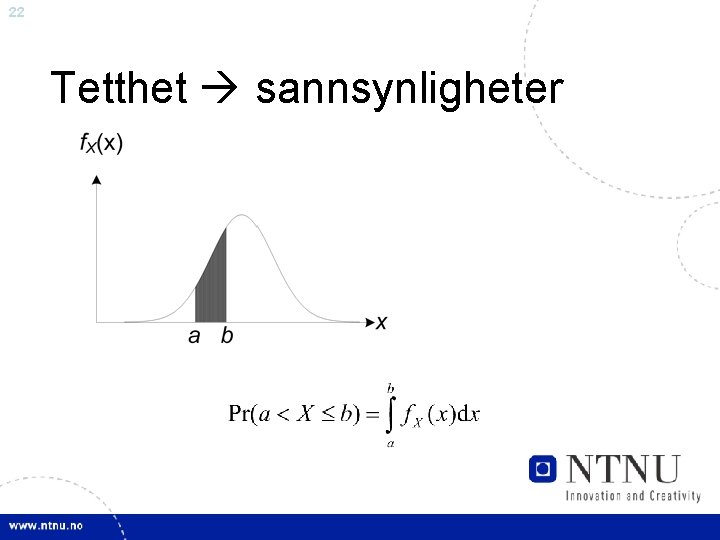
22 Tetthet sannsynligheter

23 Forventningsverdi • Forventningsverdien tilfeldig størrelse er gjennomsnittsverdien den vil anta dersom vi gjennomfører et tilfeldig forsøk (uendelig) mange ganger

24 Median og mode • Medianen tilfeldig størrelse er en verdi, Median(X), slik at sannsynligheten for at X er større enn eller lik Median(X) er lik sannsynligheten for at X er mindre enn eller lik Median(X) • Moden tilfeldig størrelse, Mode(X), er den xverdien som har størst tilhørende sannsynlighetstetthet (evt punktsannsynlighet). – Ofte betegnes Mode(X) den ”mest sannsynlige verdi”

25 Varians • Variansen tilfeldig størrelse angir variasjonen i verdien X vil anta dersom vi gjentar et tilfeldig forsøk (uendelig) mange ganger

26 Standardavvik • Standardavviket til en tilfeldig størrelse er definert ved kvadratroten av variansen

27 Fordeling av summer, produkter og maksimalverdier • Dersom X 1, X 2, …, Xn er tilfeldige størrelser, kan vi finne forventning, varians og standardavvik til summen av x-ene ved følgende formler

28 Dobbeltforventning • Dersom vi kjenner forventning og varians til X |B og X |BC, kan vi bruke setningene om dobbeltforventning: E(X) = E(X|B)*Pr(B) + E(X|BC)*Pr(BC) Var(X) = Var(X|B)*Pr(B) + Var(X|BC)*Pr(BC) + [E(X|B)-E(X)]2*Pr(B) + [E(X|BC)-E(X)]2*Pr(BC)

29 Avhengighet • Merk at ligning for varians og SD kun gjelder dersom x-ene er stokastisk uavhengig. Dersom x-ene er avhengige, må vi ta med kovariansledd for å få riktig uttrykk for variansen til summen • Var(X 1 + X 2) = Var(X 1) + Var(X 2) + 2 Cov(X 1, X 2) • hvor Cov(X 1, X 2) er kovariansen mellom X 1 og X 2 • Å ignorere uavhengighet vil typisk underestimere variansen

30 Regler for uavhengige produkter • La X 1 og X 2 være uavhengige tilfeldige størrelser, da er: – E(X 1 X 2) = E(X 1) E(X 2) – Var(X 1 X 2) = Var(X 1) E(X 2)2 + Var(X 2) E(X 1)2 + Var(X 1) Var(X 2) Var(X 1) E(X 2)2 + Var(X 2) E(X 1)2

31 Fordeling til maksimalverdier • Anta at X 1 og X 2 er tilfeldige uavhengige størrelser, og la Y = max(X 1, X 2), da er • FY(x) = Pr(Y x) = Pr(X 1 x X 2 x) = Pr(X 1 x) Pr(X 2 x) = FX 1(x) FX 2(x) • Uttrykket kan benyttes til å finne forventing og varians til maksimalverdier dersom vi kjenner fordelingen til hver av x-ene, ved standardformler forventning og varians

32 Sannsynlighetstetthet: • Vi har at f. Y(x) = FY(x)/ x, samt kjerneregelen gir: • f. Y(x)= f. X 1(x)FX 2(x) + FX 1(x)f. X 2(x) E(Y) = x [f. X 1(x)FX 2(x) + FX 1(x)f. X 2(x)]dx Var(Y) = (x-E(Y))2 [f. X 1(x)FX 2(x) + FX 1(x)f. X 2(x)]dx • Kan enkelt finnes ved numeriske metoder

33 Sannsynlighetsfordelinger • Følgende sannsynlighetsfordelinger benyttes ofte i sammenheng med prosjektrisiko: – – Normalfordelingen Gammafordelingen (=Erlangfordeling) Trekantfordeling PERT-fordeling

34 Normalfordeling • Normalfordelingen beskrives ved – E(X) = – Var(X) = 2 • Grafisk fremstilling – CDFNormal(x, E, SD) – PDFNormal(x, E, SD)

35 Trekantfordeling • • Sannsynlighetstettheten er en trekant, med L = laveste verdi M = mest sannsynlig verdi (”toppen”) H = høyeste verdi

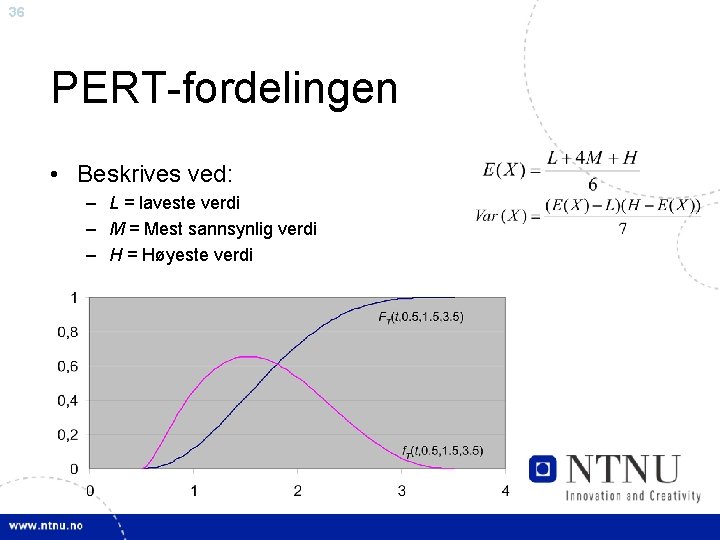
36 PERT-fordelingen • Beskrives ved: – L = laveste verdi – M = Mest sannsynlig verdi – H = Høyeste verdi

37 Gammafordeling (Erlangfordeling) • Verdiområde fra 0 til uendelig • Beskrives ofte med to parametere, og – E(X) = α/ – Var(X) = α/ 2

38 Erlang og trippel-estimat • Ofte anis Erlangfordelingen med L, M og H verdier • For Erlangfordelingen gir det ikke mening å fortolke L og H som absolutte nedre og øvre verdier • Dersom L og H fortolkes som 1% og 99% kvantiler gjelder • Dersom L og H fortolkes som 10% og 90% kvantiler gjelder