Zklady systmov relneho asu Teria asovch konench automatov

Základy systémov reálneho času Teória časových konečných automatov

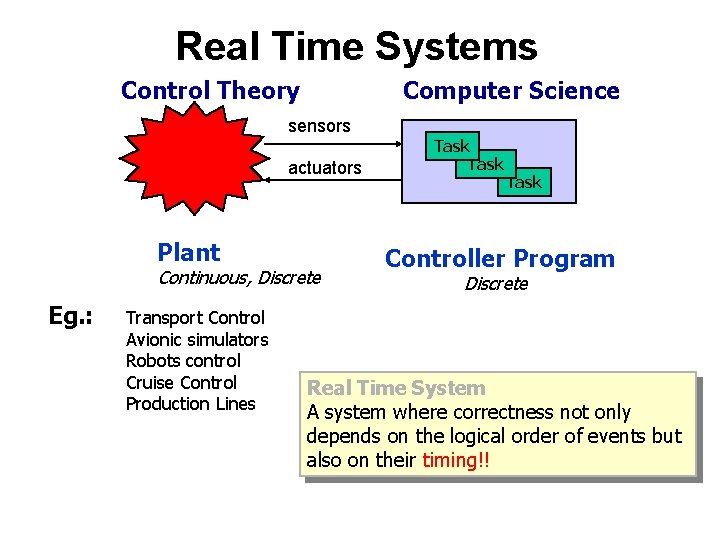
Real Time Systems Control Theory Computer Science sensors actuators Plant Continuous, Discrete Eg. : Transport Control Avionic simulators Robots control Cruise Control Production Lines Task Controller Program Discrete Real Time System A system where correctness not only depends on the logical order of events but also on their timing!!

Prechodové systémy Definícia Prechodový systém je štvorica S = (Q, Q 0, , ) kde Q je množina stavov Q 0 Q je množina počiatočných stavov je množina udalostí Q Q je množina prechodov Systém štartuje z počiatočného stavu q 0 Q 0 Prechod (q, a, q’) označujeme ako q a q’ Stav q je dosiahnuteľný stav prechodového systému ak je dosiahnuteľný z niektorého počiatočného stavu to znamená že existuje 1 n q 0 q 1 2 q 2 3 q 3… n q

Zložený systém sa tvorí ako súčin navzájom interagujúcich systémov Nech S 1 = (Q 1, Q 10, 1) S 2 = (Q 2, Q 20, 2) S 1 || S 2 = (Q 1 Q 2, Q 10 Q 20, 1 2 , ) kde (q 1, q 2) a (q 1’, q 2’) ak 1. a 1 2 a q 1 1 a q 1’ a q 2 2 a q 2’ 2. a 1 2 a q 1 1 a q 1’ a q 2’ = q 2 3. a 2 1 a q 2 2 a q 2’ a q 1’= q 1 Operátor || sa tiež nazýva aj operátor paralelnej kompozície

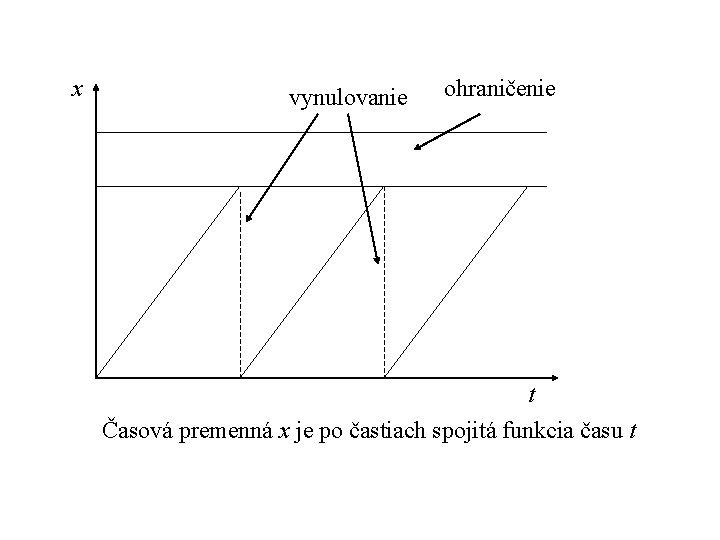
Prechodový systém s časovým ohraničením Aby sme vyjadrili vlastnosti systému v závislosti od časových ohraničení uvažujme konečný graf rozšírený o konečný počet časových premenných. Vrcholy grafu budeme volať pozície a hrany grafu prechody. Čas môže plynúť len v pozíciách pretože prechody sú okamžité. Časové premenné môžu byť položené rovné nule pre ľubovolný prechod. V každom okamžiku hodnota časovej premennej určuje uplynutí čas od jej posledného vynulovania. Každému prechodu môžeme priradiť ohraničenie nejakej časovej premennej a požadovať, že prechod sa môže uskutočniť len ak hodnota časovej premennej spĺňa toto ohraničenie. Každej pozícii priradíme ohraničenie pre ľubovolnú časovú premennú, ktoré budeme volať invariant a požadovať, že čas v danom stave môže plynúť len pokiaľ je invariant splnený.

x vynulovanie ohraničenie t Časová premenná x je po častiach spojitá funkcia času t

Definícia konečného časového automatu: Nech X je množina časových premenných a (X) je množina časových ohraničení definovaná gramatikou: kde x X a c je reálna konštanta Časový automat A je šestica (L, L 0, , X, I, E) kde L je konečná množina pozícií L 0 L je množina počiatočných pozícií je konečná množina udalostí X je konečná množina časových premenných I je zobrazenie, ktoré priradí každej pozícii nejaké časové ohraničenie z (X) E L 2 X (X) L je množina prechodov. e =( s, a , , , s’) E reprezentuje prechod z pozície s do pozície s’ v dôsledku vzniku udalosti a. je časové ohraničenie pre časové premenné z X, ktoré špecifikuje kedy je prechod možný a X určuje, ktoré časové premenné budú s prechodom vynulované.

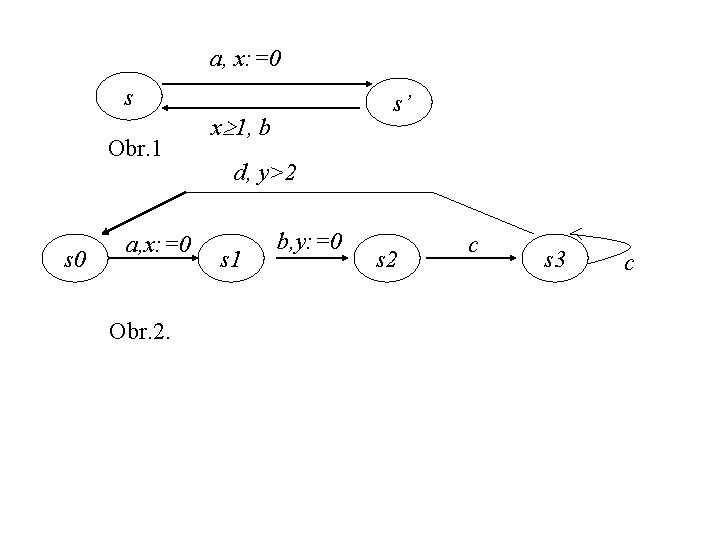
a, x: =0 s Obr. 1 s 0 a, x: =0 Obr. 2. s’ x 1, b d, y>2 s 1 b, y: =0 s 2 c s 3 c

Sémantika časového automatu je definovaná pomocou prechodového systému SA, ktorý je k automatu pridružený. Stav q prechodového systému SA je dvojica (s, ), kde s je pozícia A a je hodnota časovej premennej x, ktorá spĺňa invariant I(s). Stavy SA označujeme QA. Stav (s, ) je počiatočný ak s je počiatočná pozícia A a (x) = 0 pre všetky x. Existujú dva typy prechodov SA: • Stav sa zmení uplynutím času o časový inkrement 0: (s, ) (s, + ) ak pre všetky 0 ’ , + ’ spĺňa invariant I(s). • Stav sa zmení v dôsledku vzniku udalosti a : (s, ) a (s’, [ : =0]), ak spĺňa časové ohraničenie . Pre SA z Obr. 2 s množinou udalostí {a, b, c, d} a stavovým priestorom {s 0, s 1, s 2, s 3} R 2 niektoré prechody sú: (s 0, 0, 0) 1. 2(s 0, 1. 2) a(s 1, 0, 1. 2) 0. 7(s 1, 0. 7, 1. 9) b(s 2, 0. 7, 0) 0. 1(s 2, 0. 8, 0. 1) 0. 1(s 2, 0. 9, 0. 2)

Trajektóriou prechodového systému SA nazývame nekonečnú postupnosť stavov a prechodov: r = q 0 l 0 q 1 l 1 q 2 l 2 q 3 … kde qi Q a li ( R+) Množinu trajektórií vychádzajúcich z q označme RA(q) a množinu všetkých trajektórií SA označme RA, kde Definícia Stav q’ je dosiahnuteľný z q ak patrí do niektorej z trajektórií vychádzajúcich z q. Vlastnosť: Pre prechodový systém platí časová aditívnosť: ak q q’ a q’ q’’ potom q q’’

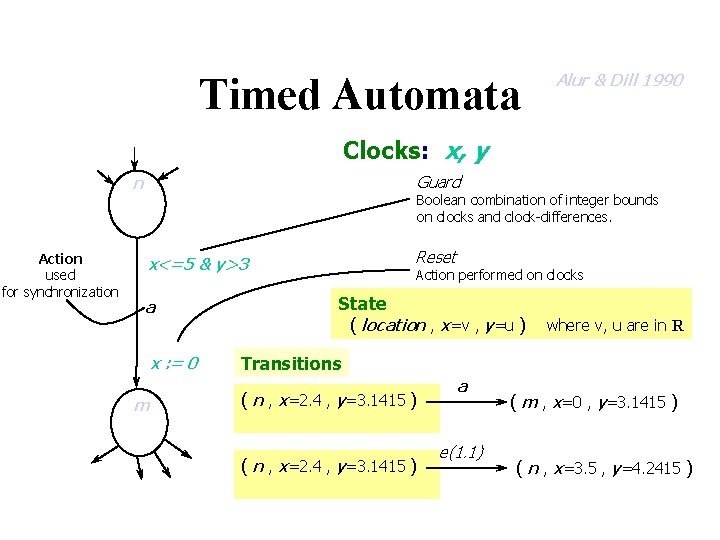
Timed Automata Alur & Dill 1990 Clocks: x, y Guard n Action used for synchronization Boolean combination of integer bounds on clocks and clock-differences. Reset x<=5 & y>3 a x : = 0 m Action performed on clocks State ( location , x=v , y=u ) where v, u are in R Transitions ( n , x=2. 4 , y=3. 1415 ) a e(1. 1) ( m , x=0 , y=3. 1415 ) ( n , x=3. 5 , y=4. 2415 )

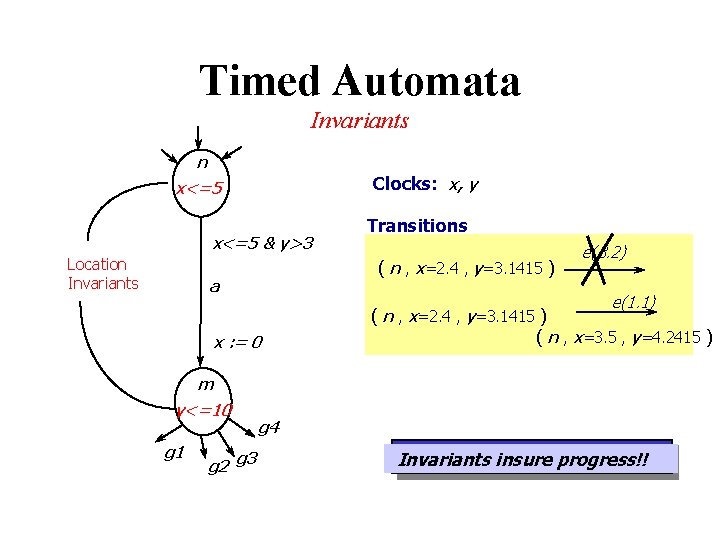
Timed Automata Invariants n Clocks: x, y x<=5 & y>3 Location Invariants Transitions ( n , x=2. 4 , y=3. 1415 ) a e(3. 2) e(1. 1) x : = 0 ( n , x=2. 4 , y=3. 1415 ) ( n , x=3. 5 , y=4. 2415 ) m y<=10 g 1 g 2 g 3 g 4 Invariants insure progress!!

Podmienky nutné pre uskutočniteľnosť prechodu: 1. Ak plynutím času v niektorom stave prestane platiť časový invariant potom musí byť umožnený niektorý prechod z tohto stavu. Nemôže napríklad nastať : I(s 0)= x<2 a (s 0, a, x>2, {0}, s 1) s 0 a, x>2 s 1 x<2 2. Z každého dosiahnuteľného stavu automatu, by mala byť prípustná možnosť časovej divergencie (neobmedzeného narastania času). x: =0 x x<2 a x: =0 x<2 a, x>1, x: =0 Automaty splňujúce tieto podmienky sa volajú non. Zeno.

Konštrukcia zložených automatov Nech A 1 = (L 1, L 10, 1, X 1, I 1, E 1) A 2 = (L 2, L 20, 2, X 2, I 2, E 2) Predpokladajme že X 1, X 2 sú dizjunktné potom A 1||A 2 = (L 1 L 2, L 10 L 20 , 1 2 , X 1 X 2 , I, E) kde I(s 1, s 2)= I(s 1) I(s 2) a prechody E sú definované: 1. pre a 1 2 (a je synchronizačná udalosť) pre všetky ( s 1, a , 1, s 1’) z E 1 a ( s 2, a , 2, s 2’) z E 2 E obsahuje ( (s 1, s 2), a , 1 2, (s 1’, s 2’)) 2. pre a 1 2 pre všetky ( s, a , , , s’) z E 1 a všetky t z L 2 E obsahuje ((s, t) a , , , (s’, t)) 3. pre a 2 1 pre všetky ( s, a , , , s’) z E 2 a všetky t z L 1 E obsahuje ((t, s) a , , , (t, s’))

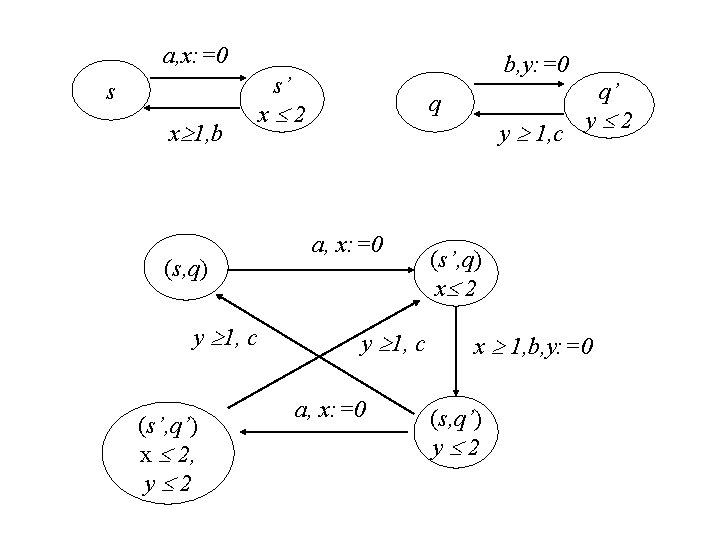
a, x: =0 b, y: =0 s’ s x 1, b (s, q) y 1, c (s’, q’) x 2, y 2 q’ q x 2 a, x: =0 y 1, c a, x: =0 y 1, c y 2 (s’, q) x 2 x 1, b, y: =0 (s, q’) y 2

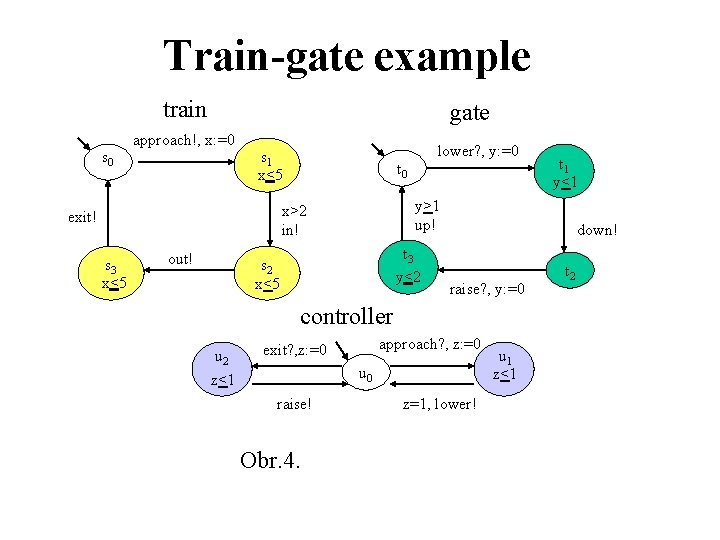
Train-gate example train s 0 gate approach!, x: =0 lower? , y: =0 s 1 x<5 t 0 y>1 up! x>2 in! exit! s 3 x<5 out! t 3 y<2 s 2 x<5 down! raise? , y: =0 controller u 2 z<1 approach? , z: =0 exit? , z: =0 u 0 raise! Obr. 4. t 1 y<1 z=1, lower! u 1 z<1 t 2

train||gait||controller Počet pozícií: 48 (nie všetky sú dosiahnuteľné) Počet udalostí: 8 {approach, in, out, exit, lower, down, raise, up} Počet čas. premenných: 3 {x, y, z} Invarianty pre dosiahnuteľné pozície: I(s 1, u 1, t 0)= x<5 z<1 I(s 1, u 0, t 1)= x<5 y<1 I(s 1, u 0, t 2)= x<5 I(s 2, u 0, t 2)= x<5 I(s 3, u 0, t 2)= x<5 I(s 0, u 2, t 2)= z<1 I(s 0, u 0, t 3)= y <2 Prechody: ((s 0, u 0, t 0), approach, 0, {x, z}, (s 1, u 1, t 0)) ((s 1, u 1, t 0), lower, z=1, {y}, (s 1, u 0, t 1)) ((s 1, u 0, t 1), down, 0, {0}, (s 1, u 0, t 2)) ((s 1, u 0, t 2), in, x>2 , {0}, (s 2, u 0, t 2)) ((s 2, u 0, t 2), out, 0, {0}, (s 3, u 0, t 2)) ((s 3, u 0, t 2), exit, 0, {z}, (s 0, u 2, t 2)) ((s 0, u 2, t 2), raise, 0, {y}, (s 0, u 0, t 3)) ((s 0, u 0, t 3), up, y>1, {0}, (s 0, u 0, t 0))

Analýza dosiahnutelnosti stavu Definícia Pozícia s časového automatu je dosiahnuteľná z počiatočnej pozície s 0 ak stav q = (s, ) prechodového systému SA je dosiahnuteľný z počiatočného stavu q 0 = (s 0, 0). Problém dosiahnuteľnosti cieľovej množiny LF L automatu A je určiť či sú pozície z LF dosiahnuteľné alebo nie. Verifikácia bezpečnosti systémov reálneho času môže byť potom formulovaná ako úloha určenia dosiahnuteľnosti neželateľných pozícií automatu. Napríklad v príklade z Obr. 4 (Train|Gate|Controller (TGC)) otázka bezpečnosti systému si vyžaduje, že vždy keď je vlak medzi závorami tie musia byť spustené. To znamená, že každý dosiahnuteľný stav TGC, ktorý obsahuje pozíciu s 2 musí obsahovať aj pozíciu t 2.

Dôkaz Z časovej analýzy grafu prechodového systému STGC zistíme, že stav (s 2, u 0, t 2) je dosiahnuteľný. Signál approach nemôže byť okamžite nasledovaný signálom in pretože v stave (s 1, u 1, t 0) časové premenné x a z majú rovnakú hodnotu 0 a teda udalosť lower s ohraničením z = 1 určite predchádza udalosť in s ohraničením x > 2. Stav (s 2, u 0, t 2) patrí do trajektórii: (s 0, u 0, t 0) approach (s 1, u 1, t 0) lower (s 1, u 0, t 1) down (s 1, u 0, t 2) in (s 2, u 0, t 2) out (s 3, u 0, t 2) exit (s 0, u 2, t 2) raise (s 0, u 0, t 3) up (s 0, u 0, t 0) Časová analýza sa pre zložité systémy, ktorých prechodový systém SA je nekonečný (časové premenné nadobúdajú hodnoty z R+ ) nedá algoritmizovať a preto je nutné pri riešení problému dosiahnuteľnosti stavu nájsť konečnú reprezentáciu časového automatu.

Zónový automat Časová zóna je množina hodnôt časových premenných vyjadrená konjunkciou ohraničení časových premenných a ich diferencií. Časová zóna je generovaná gramatikou: Vlastnosti časových zón: • Časová zóna je konvexná množina v k-rozmernom priestore, kde k je počet časových premenných. • Každé ohraničenie v invariante pozície a ohraničenie časových premenných v prechode automatu je časová zóna. • Ak zjednotenie dvoch časových zón je konvexné potom je to časová zóna. • Prienik dvoch časových zón je časová zóna.

Zones Operations with zones Delay: Projection: Conjunction:

Význam operácii nad zónami: Delay (plynutie času): Pre časovú zónu , označuje množinu interpretácií časových premenných d, d R získanú plynutím času pre časové premenné tvoriace časovú zónu. je zóna. Projection (projekcia): Pre podmnožinu { } časových premenných časovej zóny { } znamená množinu interpretácií časových premenných n[ : =0]. { } je zóna. Conjunction (konjunkcia): Prienik dvoch časových zón a je opäť zóna

Zóna je dvojica (s, ) pozostávajúca z pozícii s a časovej zóny . Vytvoríme prechodový systém, ktorého stavmi sú zóny nasledovne: Nech je nasledujúca zóna succ( , e) prechod automatu e E, e =( s, a , , , s’) definovaná krokmi: 1. Urobí sa prienik s invariantom pozície s 2. Na výsledok sa aplikuje operáciu delay 3. Urobí sa prienik výsledku s invariantom pozície s 4. Urobí sa prienik výsledku s ohraničením prechodu e 5. Vynulujú sa všetky časové premenné z množiny Množina succ( , e) interpretácií časových premenných je časová zóna. Definícia Zónový automat Z(A) je prechodový systém, ktorého stavy sú zóny. Pre každú počiatočnú pozíciu s časového automatu A je (s, [X: =0]) počiatočným stavom Z(A) a pre každý prechod e =( s, a , , , s’) časového automatu A a každú časovú zónu , ez = ((s, ), a, (s’, succ( , e))) je prechod Z(A).

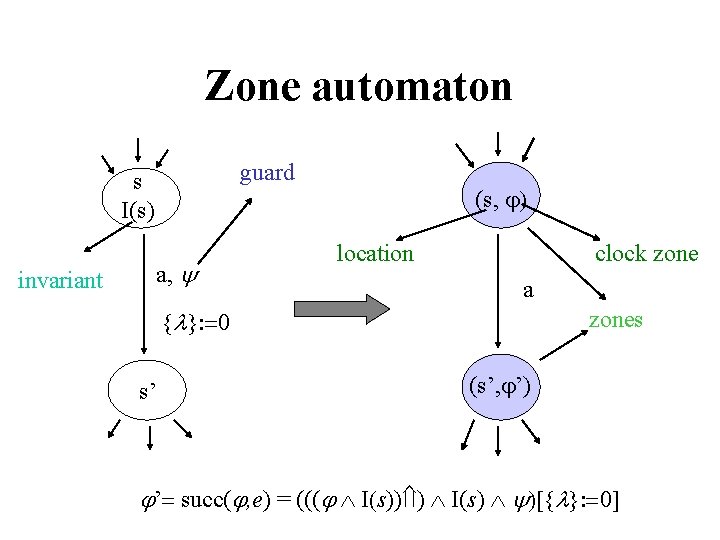
Zone automaton guard s I(s) invariant a, (s, j) location clock zone a { }: =0 s’ zones (s’, j’) ’= succ( , e) = ((( I(s)) ) I(s) )[{ }: =0]

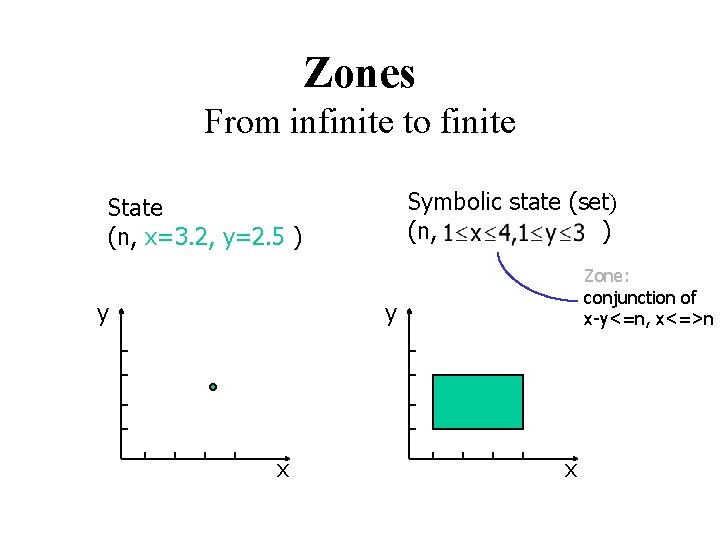
Zones From infinite to finite Symbolic state (set) (n, ) State (n, x=3. 2, y=2. 5 ) y Zone: conjunction of x-y<=n, x<=>n y x x

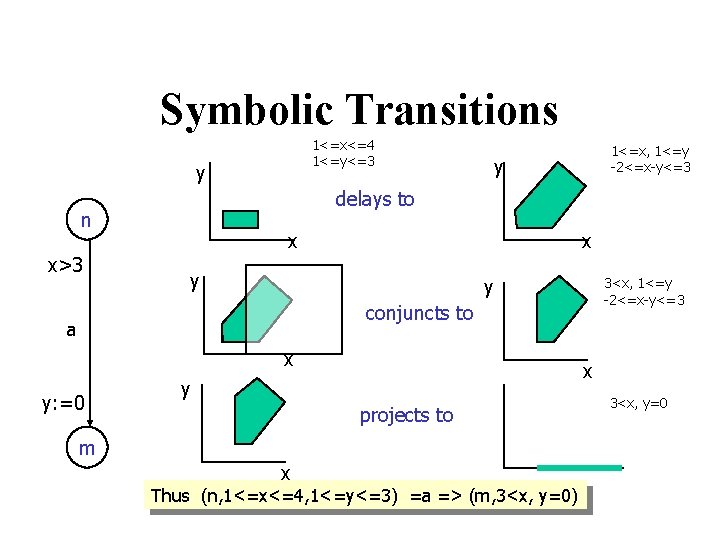
Symbolic Transitions 1<=x<=4 1<=y<=3 y y delays to n x>3 1<=x, 1<=y -2<=x-y<=3 x x y y 3<x, 1<=y -2<=x-y<=3 conjuncts to a x y: =0 x y projects to m x Thus (n, 1<=x<=4, 1<=y<=3) =a => (m, 3<x, y=0) 3<x, y=0

Algoritmus dosiahnutelnosti stavu automatu A Definícia Pozícia s časového automatu A je dosiahnuteľná z počiatočnej pozície s 0 ak stav (zóna) q = (s, ) prechodového systému Z(A) je dosiahnuteľný z počiatočného stavu (zóny) q 0 = (s 0, 0). Teda existuje postupnosť prechodov ez 1, ez 2, . . . , ezn prechodového systému Z(A) taká, že q 0 ez 1 q 1 ez 2 q 2 . . . ezn q. Algoritmus Tvorí sa postupnosť množín zón Z 0 Z 1 . . . taká, že Z 0 = q 0 Zi+1 = Zi Suc( Zi) kde Suc( Zi)= {q| qi Zi, qi ez q}. Tvrdenie Pre s, s 0 L, q Reach(q 0) iff q i 0 Zi

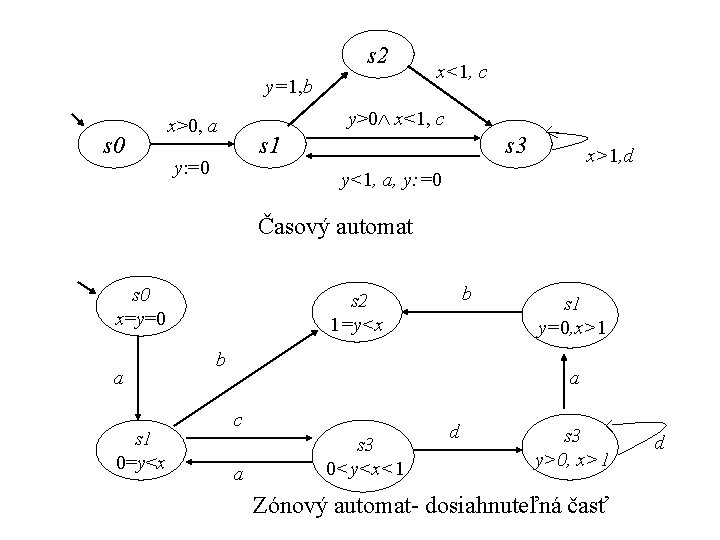
s 2 y=1, b s 0 x<1, c y>0 x<1, c x>0, a s 1 y: =0 s 3 x>1, d y<1, a, y: =0 Časový automat s 0 x=y=0 a s 1 0=y<x b s 2 1=y<x b s 1 y=0, x>1 a c a s 3 0<y<x<1 d s 3 y>0, x>1 Zónový automat- dosiahnuteľná časť d

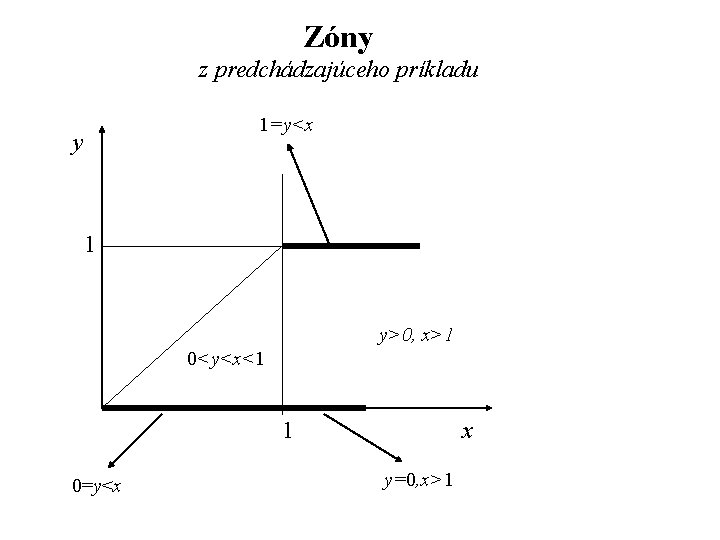
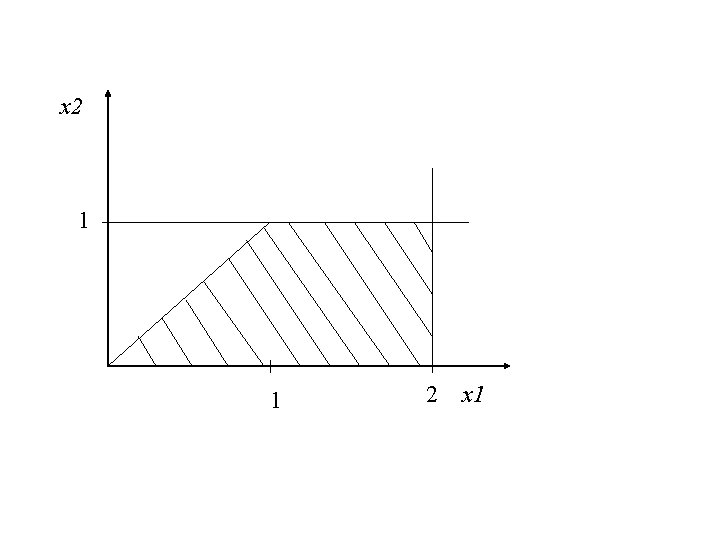
Zóny z predchádzajúceho príkladu 1=y<x y 1 y>0, x>1 0<y<x<1 1 0=y<x x y=0, x>1

Reprezentácia časových zón Diferenčné matice ohraničení Časová zóna pre k- časových premenných je reprezentovaná (k+1) rozmernou maticou D. Prvky matice D sa určia nasledovne: Pre každé i, di 0 je horná hranica xi a d 0 i je dolná hranica xi Pre každú dvojicu i, j, dij určuje hornú hranicu diferencie xi-xj Symbol sa udáva v prípade keď horná hranica je nie daná. Ostrá a neostrá nerovnosť sa určujú číslicami 1 a 0 ako druhým prvkom v dvojici (dij, 1) alebo (dij, 0). Pr. Časová zóna

x 2 1 1 2 x 1

môže byť reprezentovaná maticou: Reprezentácia ale nie je jednoznačná. Uvedené ohraničenia môžu byť „sprísnené“, napr. keďže x 1<2, tak x 1 -x 2<2, ďalej suma diferencií xi-xj a xj- xl je horná hranica diferencie xi-xl, tým získame nasledovnú ekvivalentnú maticu:

Kanonické matice Matica D je splniteľná ak reprezentuje neprázdnu časovú zónu. Ak D je nesplniteľná matica potom existuje postupnosť indexov 0 i 1, i 2, . . . ij k takých, že di 1, i 2 +di 2, i 3+. . . +dij, i 1< (0, 1) Pričom (i, j)< (i’, j’) iff ak i< i’ alebo i= i’ a j< j’ a (i, j)+(i’, j’)= (i+ i’, j j’) Matica je kanonická iff Každá splniteľná matica má ekvivalentnú kanonickú maticu. Dve kanonické matice D a D’ sú ekvivalentné iff dij = dij’.

Operácie nad diferenčnými maticami V algoritme pre dosiahnuteľnosť stavu prechod e je potrebné počítať nasledovnú časovú zónu succ( , e). Ďalej ukážeme ako sa počítajú operácie nad časovými zónami ak sú reprezentované pomocou diferenčných matíc. Conjunction: Matica D’’ reprezentuje operáciu konjunkcie nad zónami, ktoré sú reprezentované maticami D a D’. Prvky matice D’’ sú d’’ij = min (dij, d’ij). Výslednú maticu je treba kanonizovať. Delay: D prvky di 0 sa zmenia na ostatné zostanú nezmenené. Výslednú maticu je nutné kanonizovať. Projection: { }D Pre xi di 0 a d 0 i sa zmení na (0, 1), pre xi, xj , dij sa zmení na (0, 1), pre xi a xj sa zmení dij na d 0 j a dji na dj 0. Výslednú maticu je treba kanonizovať.

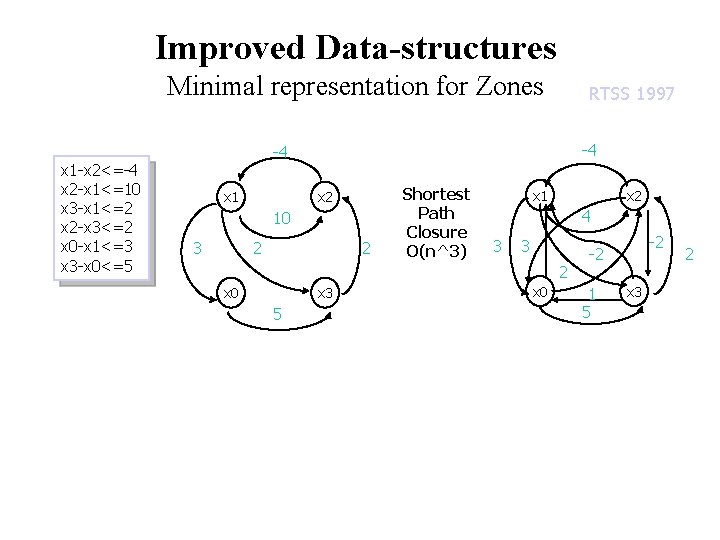
Improved Data-structures Minimal representation for Zones x 1 -x 2<=-4 x 2 -x 1<=10 x 3 -x 1<=2 x 2 -x 3<=2 x 0 -x 1<=3 x 3 -x 0<=5 RTSS 1997 -4 -4 x 1 x 2 10 3 2 2 Shortest Path Closure O(n^3) x 1 x 2 4 3 3 2 x 0 x 3 5 x 0 -2 -2 1 5 x 3 2

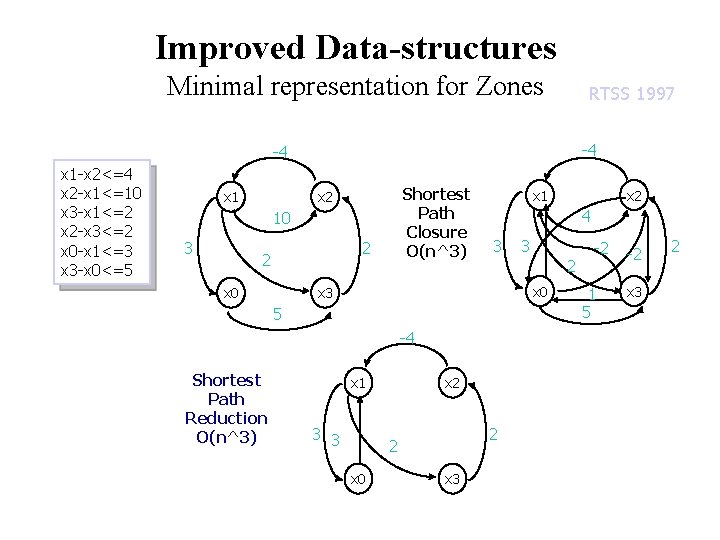
Improved Data-structures Minimal representation for Zones RTSS 1997 -4 -4 x 1 -x 2<=4 x 2 -x 1<=10 x 3 -x 1<=2 x 2 -x 3<=2 x 0 -x 1<=3 x 3 -x 0<=5 x 1 Shortest Path Closure O(n^3) x 2 10 3 2 2 x 0 x 1 4 3 3 2 x 0 x 3 5 -4 Shortest Path Reduction O(n^3) x 1 3 3 x 2 2 2 x 0 x 3 x 2 -2 1 5 -2 x 3 2

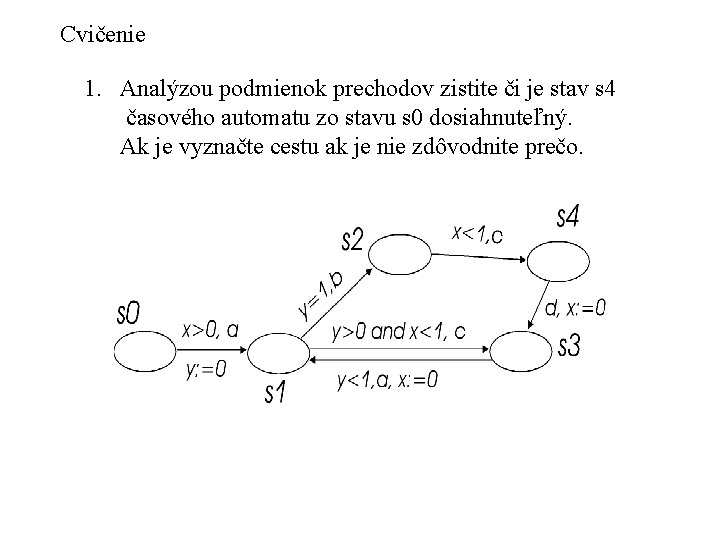
Cvičenie 1. Analýzou podmienok prechodov zistite či je stav s 4 časového automatu zo stavu s 0 dosiahnuteľný. Ak je vyznačte cestu ak je nie zdôvodnite prečo.

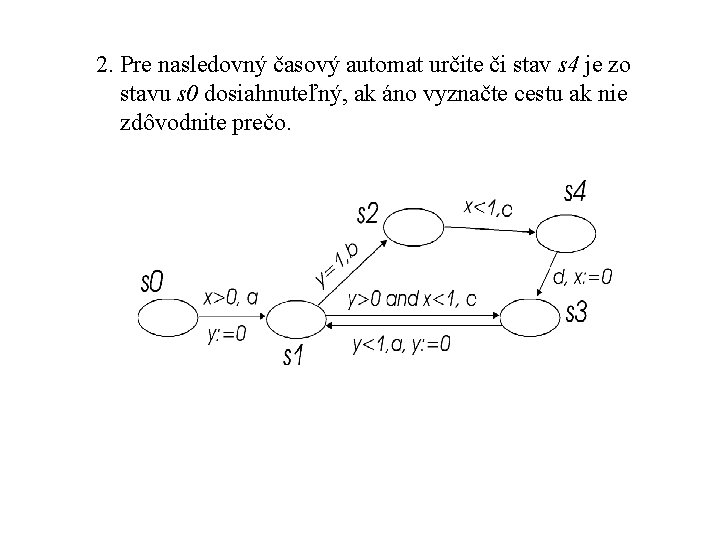
2. Pre nasledovný časový automat určite či stav s 4 je zo stavu s 0 dosiahnuteľný, ak áno vyznačte cestu ak nie zdôvodnite prečo.

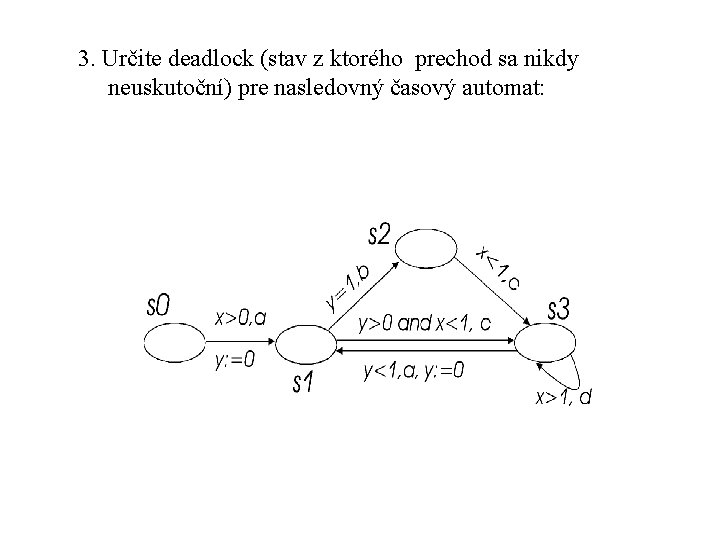
3. Určite deadlock (stav z ktorého prechod sa nikdy neuskutoční) pre nasledovný časový automat: