Wprowadzenie do Algorytmiki Sortowanie 2 Dr in Szymon

Wprowadzenie do Algorytmiki Sortowanie 2 Dr inż. Szymon Wąsik

Praca w ciągu tygodnia l Rafał Promiński (x 2) l Marcin Zatorski (x 2) l Oskar Firlej

Quick. SORT l Wybieramy pewien element i na lewo od niego wrzucamy elementy mniejsze, na prawo większe l Dalej postępujemy rekurencyjnie

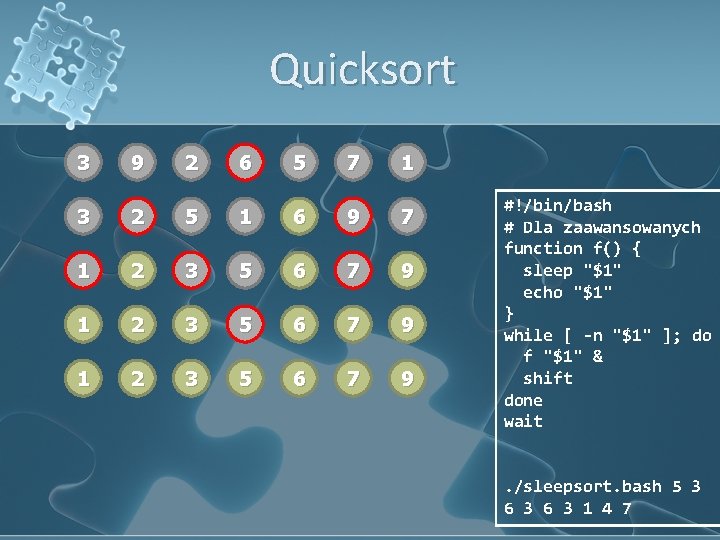
Quicksort 3 9 2 6 5 7 1 3 2 5 1 6 9 7 1 2 3 5 6 7 9 #!/bin/bash # Dla zaawansowanych function f() { sleep "$1" echo "$1" } while [ -n "$1" ]; do f "$1" & shift done wait. /sleepsort. bash 5 3 6 3 1 4 7

Quicksort Wartość elementu granicznego (w czerwonym kółku) Szukamy pierwszego niepasującego z lewej i ostatniego z prawej Sortujemy rekurencyjnie quicksort(a[], first, last) l ← first r ← last v ← a[(l + r) div 2] do while a[l] < v l++ while v < a[r] r-if l <= r swap(a[l], a[r]) l++ r-while l <= r if l < last quicksort(a, l, last) if first < r quicksort(a, first, r)

Quicksort l Czas działania – średni O(n lg n) l Pesymistyczny czas działania O(n 2) – trudny do osiągnięcia (aby go uniknąć wystarczą podziały w stosunku 1: stała) l Sortuje w miejscu - wymaga stałej ilości dodatkowej pamięci (jeżeli zaimplementujemy go iteracyjnie)

Statystyki pozycyjne l Dany jest nieposortowany ciąg n liczb l Wyznacz k-tą co do wartości liczbę w ciągu l Stosujemy algorytm Quick. Sort, ale po podziale sortujemy tylko tą część ciągu, do której należy k-ty element l Czas działania: O(n)

Sortowanie przez zliczanie l Pomocne jedynie gdy mamy mały zakres dyskretnych wartości l Zlicza ile mamy elementów o kolejnych wartościach l Dla ciągu: 1, 2, 4, 2, 3, 1, 3, 4, 2, 1, 2 mamy: trzy 1, cztery 2, dwie 3 i dwie 4 l Możemy wywnioskować, że trzy pierwsze elementy w ciągu posortowanym to jedynki, następne cztery to dwójki, itd.

Sortowanie przez zliczanie Zliczamy liczbę wystąpień każdej wartości Tworzymy ciąg sum częściowych Wpisujemy elementy na właściwe miejsce Kopiujemy wynik do sortowanej tablicy counting_sort(n, a[]) for i ← 1. . n c[a[i]]++ for i ← 2. . n c[i] ← c[i-1] + c[i] for i ← 1. . n b[c[a[i]]] ← a[i] c[a[i]]-for i ← 1. . n a[i] ← b[i]

Sortowanie przez zliczanie l Sortowanie w czasie liniowym l Można je zastosować tylko w niektórych przypadkach l Wymaga liniowej, dodatkowej pamięci

Sortowanie pozycyjne l l l Posortuj liczby po ostatniej cyfrze Potem posortuj po przedostatniej cyfrze stabilnie, gwarantuje to, że np. dla 57 i 59, 57 znajdzie się przed 59, bo tak je ustawiliśmy sortując po ostatniej cyfrze Kod: radix_sort(n, d, a[]) for i ← d. . 1 counting_sort(n, a, i) Sortowanie przez zliczanie porównuje po cyfrze i-tej, d ilość cyfr Czas działania liniowy, przy nie za dużym d Zazwyczaj d = O(lg m), wtedy czas działania O(n lg m)

Sortowanie kubełkowe l Można je zastosować, gdy mamy dany ciąg o rozkładzie jednostajnym l Dzielimy zakres n liczb na wejściu na n przedziałów (kubełków). Np. dla 100 liczb rzeczywistych z przedziału <0; 1), kolejne kubełki to: <0; 0. 01), <0. 01; 0. 02), … l Kolejne liczby wrzucamy do odpowiedniego kubełka i sortujemy je wewnątrz kubełków przez scalanie l Czas działania - liniowy

Kopce l Inne nazwy: stóg, kolejka priorytetowa, ang. heap, priority queue l Szybkie wykonywanie operacji pobrania największego elementu ze zbioru l Wykorzystuje reprezentację za pomocą drzewa binarnego (nie BST!)

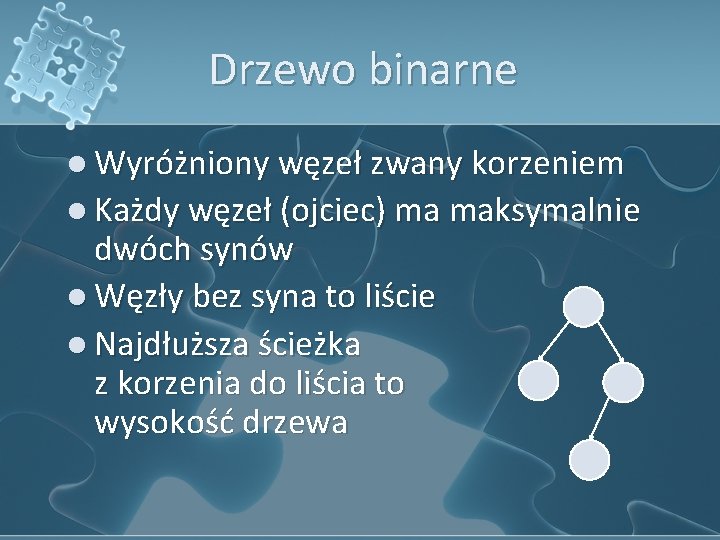
Drzewo binarne l Wyróżniony węzeł zwany korzeniem l Każdy węzeł (ojciec) ma maksymalnie dwóch synów l Węzły bez syna to liście l Najdłuższa ścieżka z korzenia do liścia to wysokość drzewa

Kopiec l Wszystkie poziomy drzewa, z wyjątkiem ostatniego są w pełni zapełnione l Na ostatnim poziomie elementy dosunięte są do strony lewej

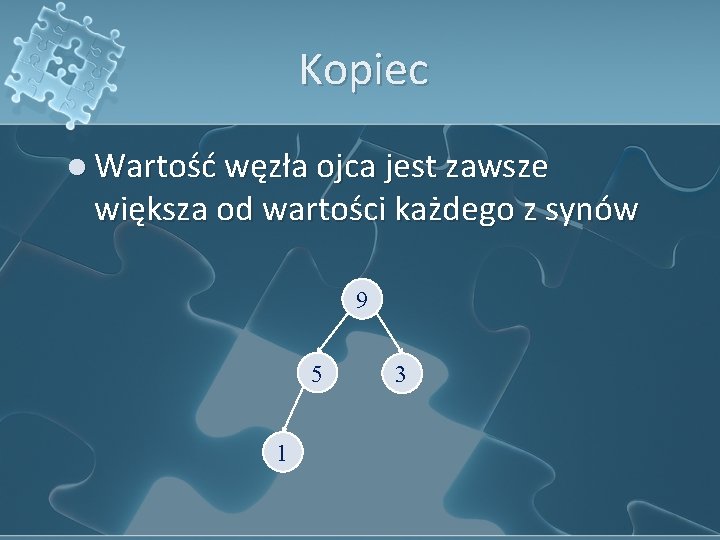
Kopiec l Wartość węzła ojca jest zawsze większa od wartości każdego z synów 9 5 1 3

Kopiec l Ponumerujmy węzły kolejnymi poziomami l Jeżeli o to numer ojca, a s 1 i s 2 to numery synów, to: 9 o = s 1 = 2 s 2 = 2 / * * 2 = s 2 / 2 o o + 1 5 1 4 2 1 3 3

Kopiec l Umiemy wyliczyć indeks ojca i syna l Numeracja jest ciągła l Możemy reprezentować kopiec za pomocą tablicy: v[] = [9; 5; 3; 1] w C: [0; 9; 5; 3; 1] ile = 4 9 5 1 4 2 1 3 3

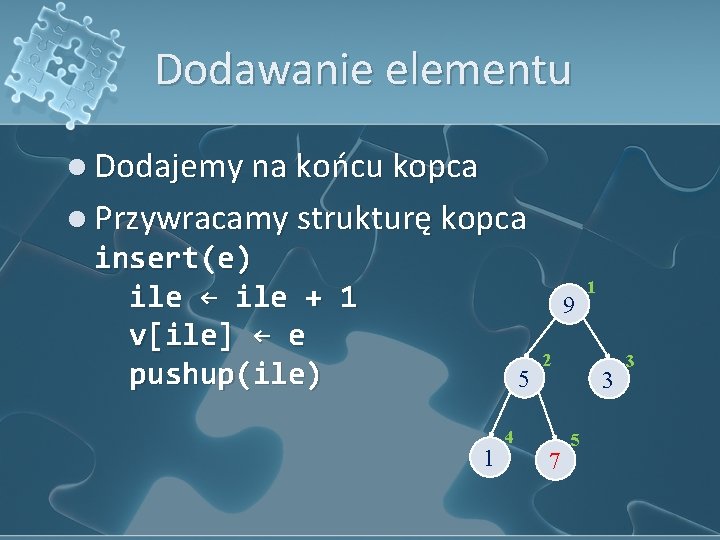
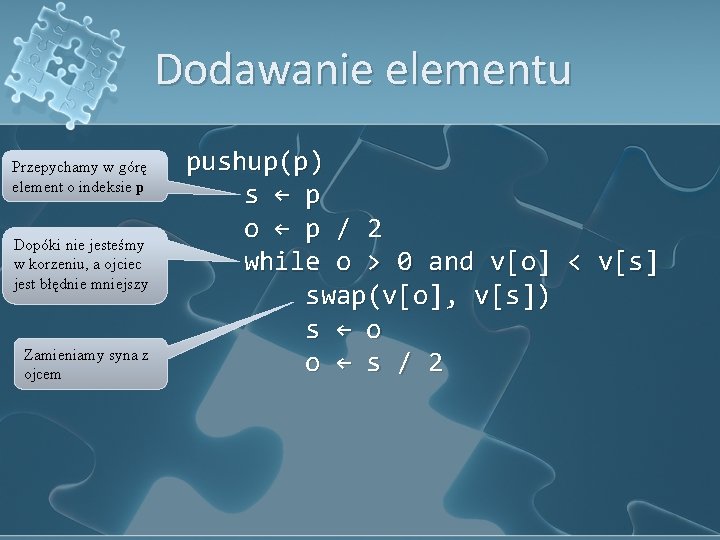
Dodawanie elementu l Dodajemy na końcu kopca l Przywracamy strukturę kopca insert(e) ile ← ile + 1 v[ile] ← e pushup(ile) 9 5 1 2 4 7 1 3 5 3

Dodawanie elementu Przepychamy w górę element o indeksie p Dopóki nie jesteśmy w korzeniu, a ojciec jest błędnie mniejszy Zamieniamy syna z ojcem pushup(p) s ← p o ← p / 2 while o > 0 and v[o] < v[s] swap(v[o], v[s]) s ← o o ← s / 2

Funkcja swap l Implementacja 1: void swap(int &a, int &b) { int c = a; a = b; b = c; } l Implementacja 2: void swap(int &a, int &b) { if (a - b) a ^= b ^= a ^= b; } l Implementacja 3: #include <algorithm>

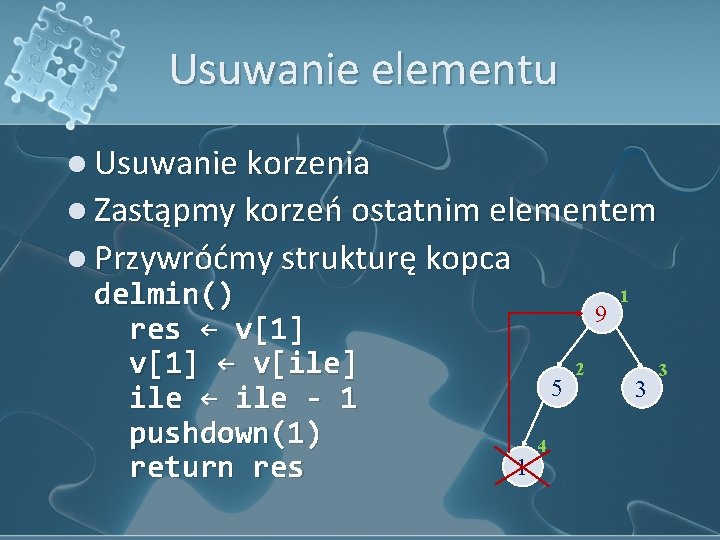
Usuwanie elementu l Usuwanie korzenia l Zastąpmy korzeń ostatnim elementem l Przywróćmy strukturę kopca delmin() res ← v[1] ← v[ile] ile ← ile - 1 pushdown(1) return res 9 5 1 4 2 1 3 3

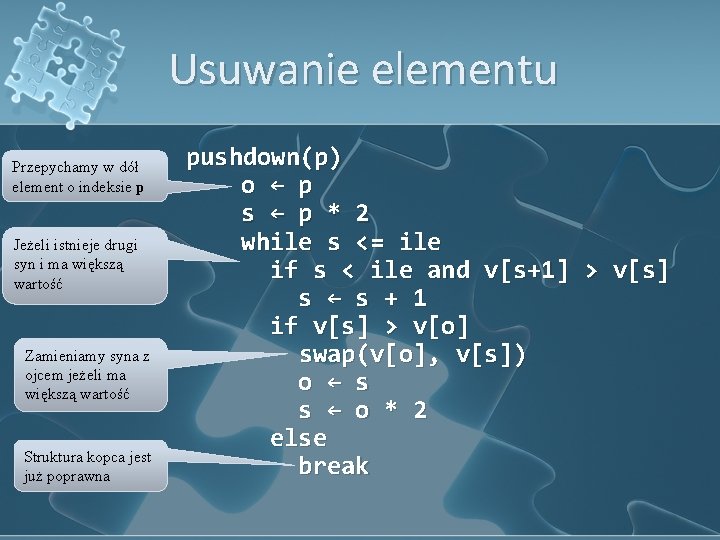
Usuwanie elementu Przepychamy w dół element o indeksie p Jeżeli istnieje drugi syn i ma większą wartość Zamieniamy syna z ojcem jeżeli ma większą wartość Struktura kopca jest już poprawna pushdown(p) o ← p s ← p * 2 while s <= ile if s < ile and v[s+1] > v[s] s ← s + 1 if v[s] > v[o] swap(v[o], v[s]) o ← s s ← o * 2 else break

Czas działania l Wysokość kopca jest logarytmiczna l Wstawianie: O(log n) l Usuwanie: O(log n) l Pobieranie największego: O(1) l Tworzenie kopca n-elementowego: O(n log n)

Przyspieszanie inicjalizacji ile ← n for i ← n. . 1 v[i] = dane[i] pushdown(i) Liczba operacji: n/2 * 1 + n / 4 * 2 + n / 8 * 3 + 1 * log n = = 1/2 + 2/4 + 3/8 + 4/16 + 5/32 + … l Czas działania: O(n) l

Kopiec dla dużych struktur l Dane są struktury: l priorytet – int, 4 bajty, pole pr l opis zadania – tablica, 996 bajtów l Każda operacja swap musi zamienić z sobą całe 1000 bajtów l Można prościej?

Kopiec dla dużych struktur l Wprowadźmy dodatkową tablicę k[] (key), która będzie trzymała porządek elementów na kopcu l k[i] = j oznacza, że element i-ty w kopcu znajduje się na pozycji j w danych wejściowych l Początkowo k[i] = i

Kopiec dla dużych struktur pushup(p) s ← p o ← p / 2 while o > 0 and v[k[o]]. pr < v[k[s]]. pr swap(k[o], k[s]) s ← o o ← s / 2

Zwiększanie wart. elementu l Wariant 1: l Dodajemy na kopiec kopię elementu z większą wartością l Zdejmując element ze stosu sprawdzamy, czy jego wartość jest aktualna (czy to nie jest ta wcześniejsza kopia z mniejszą wartością) l Wariant 2: l Wiemy gdzie w kopcu nasz element się znajduje l Zwiększamy go i przepychamy w górę

Optymalne zwiększanie wart. l Wariant 2 nie generuje dodatkowych kopii elementów l Potrzebna tablica w[] (where) oznaczająca gdzie znajduje się dany element l w[i] = j oznacza, że element i-ty w danych wejściowych znajduje się na pozycji j w kopcu

Optymalne zwiększanie wart. l Początkowo w[i] = i l Ciekawostka: zawsze w[k[i]] = i inc(i, new. V) v[i]. pr = new. V pushup(w[i])

Zwiększanie wart. elementu pushup(p) s ← p o ← p / 2 while o > 0 and v[k[o]]. pr < v[k[s]]. pr swap(k[o], k[s]) w[k[o]] = o w[k[s]] = s s ← o o ← s / 2

Łączenie dwóch kopców l Operacja Union l Skonstruuj nowy kopiec z połączonych elementów l Czas: O(n) l Kopce dwumianowe: l Łączenie w czasie O(log n) l Znajdowanie maksimum również O(log n)

Więcej o kopcach l Kopce Fibonacciego: l Operacja usuwania minimum O(log n) l Reszta operacji O(1) l Duża stała i masakryczna implementacja l Kopce można łatwo wykorzystać do sortowania liczb: l Utwórz kopiec l Wykonaj n razy operację usunięcie minimum l Czas działania: O(n log n) l Stabilne, w miejscu

Zadanie – roboty drogowe l Do wykonania są naprawy fragmentów dróg l Każdy fragment remontowany jest 1 dzień l Siła zniszczenia fragmentu to pi l Remont odcinka można rozpocząć dopiero w dniu di l Najgorsze odcinki mają być naprawione najszybciej l Jaka będzie kolejność remontowania?