Wprowadzenie do Algorytmiki Proste algorytmy dr in Szymon

Wprowadzenie do Algorytmiki Proste algorytmy dr inż. Szymon Wąsik

Praca w ciągu tygodnia l Mikołaj Sienkiewicz

Praca w ciągu tygodnia l Mikołaj Sienkiewicz l Patryk Stasiewski

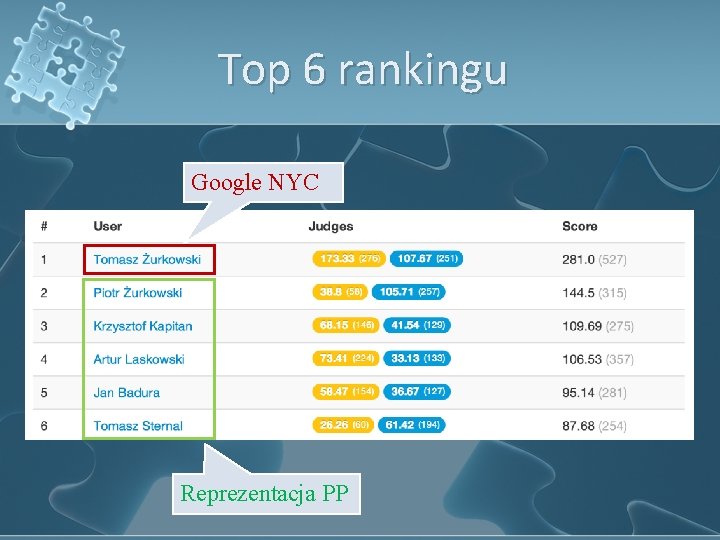
Top 6 rankingu Google NYC Reprezentacja PP

Liczby pierwsze Once it was mentioned on CNN that the new prime number discovered recently is four times bigger than the previous record! l Podzielna wyłącznie przez 1 i samą siebie l Większa od 1 l Największa znana liczba pierwsza ma 17’ 425’ 170 cyfr (dwa lata temu: 12’ 978’ 189 cyfr)

Rozkład na czynniki pierwsze l Czynnik pi występuje ni razy w liczbie x l Liczba dzielników (jakichkolwiek) liczby wynosi: (n 1 + 1) * (n 2 + 1) * … l Przykład: 12 = 22 * 31 (2 + 1) * (1 + 1) = 3 * 2 = 6 6 dzielników: 1, 2, 3, 4, 6, 12

Rozkład liczby n! l n! (n silnia) l n! = 1 * 2 * 3 * … * n l W rozkładzie liczby n! na czynniki liczba pierwsza p występuje następującą liczbę razy:

Rozkład liczby n! l Ile razy występuje 5 w rozkładzie (27!)? l 27 div 5 + 27 div 25 = l=5+1=6 l Sprawdzenie: l 27! = 1 * … * 5 * … * 10 * … * 27 = l = 5 * 10 * 15 * 20 * 25 * X = l = 5 * 5 * 52 * Y = l = 56 * Y

Spostrzeżenie 1 l Jeżeli: to: n = p* q min(p, q) <= sqrt(n) l sqrt(n) to pierwiastek kwadratowy z n

Test pierwszości 1 Spostrzeżenie 1 Jeżeli i dzieli n, to liczba złożona Nic nie dzieli n bool is. Prime(int n) if (n < 2) return for (int i = 2; i if (n % i == 0) return true; } { false; * i <= n; i++) return false;

Sito Eratostenesa http: //pl. wikipedia. org/w/index. php? title=Plik: Sieve_of_Eratosthenes_animation. gif

Sito Eratostenesa Zakładamy że wszystkie liczby oprócz 0 i 1 są pierwsze Spostrzeżenie 1 Wykreślamy wielokrotności liczb pierwszych void sito() { for (int i = 0; i <= MAXN; i++) is. Prime[i] = true; is. Prime[0] = is. Prime[1] = false; for (int i = 2; i * i <= MAXN; i++) if (is. Prime[i]) { j = i * i; while (j <= MAXN) is. Prime[j] = false, j += i; } }

Test pierwszości 2 Tworzymy listę liczb pierwszych void sito() {. . . for (int i = 0; i <= MAXN; i++) if (is. Prime[i]) primes[np++] = i; } bool is. Prime. Sito(int n) { if (n < 2) return false; for (int i = 0; (i < np) && (primes[i] * primes[i] <= n); i++) if (n % primes[i] == 0) return false; return true; }

Testy pierwszości l Sprawdzenie wszystkich potencjalnych dzielników wykonuje ok. sqrt(n) operacji l Pierwszy szybki algorytm: ASK (2002) – log 12(n) operacji l Aktualnie najszybszy algorytm: log 6(n) operacji l Potencjalnie najszybszy algorytm: log 4(n) operacji (zależny od hipotezy Riemanna)

Rekurencja Aby zrozumieć rekurencję, trzeba zrozumieć rekurencję…

Rekurencja l Wywoływanie funkcji przez samą siebie l Warunek stopu (kończący rekurencję) l Wywołanie rekurencyjne

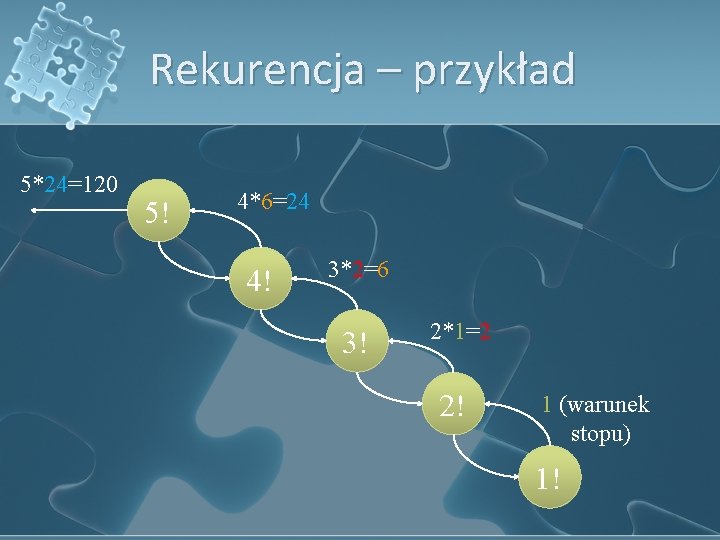
Rekurencja - przykład l Obliczanie silni: n! = 1 * 2 * … * (n-1) * n = (n-1)! * n l Rozwiązanie: int silnia(int n) { if (n == 1) return 1; return n * silnia(n-1); }

Rekurencja – przykład 5*24=120 5! 4*6=24 4! 3*2=6 3! 2*1=2 2! 1 (warunek stopu) 1!

Rekurencja l Zaleta: l prostota kodu l czytelność kodu l Wady: l trochę wolniejsze l pamięciożerne

Największy wspólny dzielnik l Algorytm naiwny – jeżeli x dzieli a oraz b, to dzieli również |a-b| l Odejmujmy od większej liczby mniejszą: while (a != b) if (a < b) b -= a; else a -= b; l Rekurencyjnie: int nwd(int a, int b) { if (a == b) return a; return nwd(max(a, b)-min(a, b), min(a, b)); }

NWD - przykład l 15 12 l 39 l 36 l 33

NWD - przykład l 1000 1 l 999 1 l 998 1 l 997 1 l 996 1 l 995 1 l 994 1 l…

Algorytm Euclidesa l Wykorzystajmy modulo! l Operator ? w C: (cond) ? a : b; zwraca a, jeżeli warunek cond jest spełniony, w przeciwnym przypadku b l Rozwiązanie: int nwd(int a, return (b == nwd(b, a % } int b) { 0) ? a : b);

Potęgowanie liczb l Podnieś liczbę a do potęgi b: res = 1; for (int i = 1; i <= b; i++) res *= a; l Lub (uwaga – strata dokładności na liczbach niecałkowitych): #include <cmath>. . . res = exp(b * log(a))

Zapis binarny (bitowy) liczb l 1310 = 11012 bo 13 = 1*23 + 1*22 + 0*21 + 1*20 lub 13 = 1*101 + 3*100 l Obliczamy biorąc resztę z dzielenia przez 2 (od końca): 13 / 2 = 6 r 1 6/2=3 r 0 3/2=1 r 1 1/2=0 r 1

Szybkie potęgowanie l 383 = 31+2+16+64 = 31 * 32 * 316 * 364 l Wystarczy obliczyć: 31, 32, 34, 38, 316, 332, 364 (każda liczba jest kwadratem poprzedniej) l Zamiast 83 operacji mnożenia, wykonujemy 10 l Q: Które potęgi dwójki wykorzystać? A: Te, które odpowiadają jedynkom w zapisie binarnym

Szybkie potęgowanie Sprawdzamy, czy kolejny bit w zapisie binarnym jest równy 1 Obliczamy kolejny kwadrat podstawy // a – podstawa, b - wykładnik int pow(int a, int b) { int pow_a = a; int res = 1; while (b > 0) { if (b % 2 == 1) res *= pow_a; b /= 2; pow_a *= pow_a; } return res; }

Liczby Fibonacciego l F(1) = 1 F(2) = 1 F(n) = F(n-1) + F(n-2) l Prosty algorytm obliczający: f[0] = 1; f[1] = 1; for (int i = 2; i < n; i++) f[i] = f[i-1] + f[i-2];

Liczby Fibonacciego l F(1) = 1 F(2) = 1 F(n) = F(n-1) + F(n-2) l Tragiczny algorytm obliczający: int fib(int n) { if (n < 2) return 1; return fib(n-1) + fib(n-2); }

Mnożenie macierzy l Macierz = tablica l Mnożenie macierzy o wymiarach a x b przez macierz b x c daje macierz a x c. Uwaga: wymiar b musi być taki sam. l Element (i, j) macierzy wynikowej to rezultat mnożenie i-tego wiersza pierwszej macierzy przez j-tą kolumnę drugiej

Liczby Fibonacciego l N-ta liczba, to liczby na przekątnej macierzy: l Na przykład F(10) = 55: l Wykorzystajmy szybkie potęgowanie!

Liczby o dużej dokładności l 64 bitowe liczby całkowite: -9, 2*1018 <= long <= 9, 2*1018 0 <= unsigned long <= 18, 4*1018 l IO: %lld, %llu l Deklarowanie: typedef long LL; typedef unsigned long ULL; ULL a;

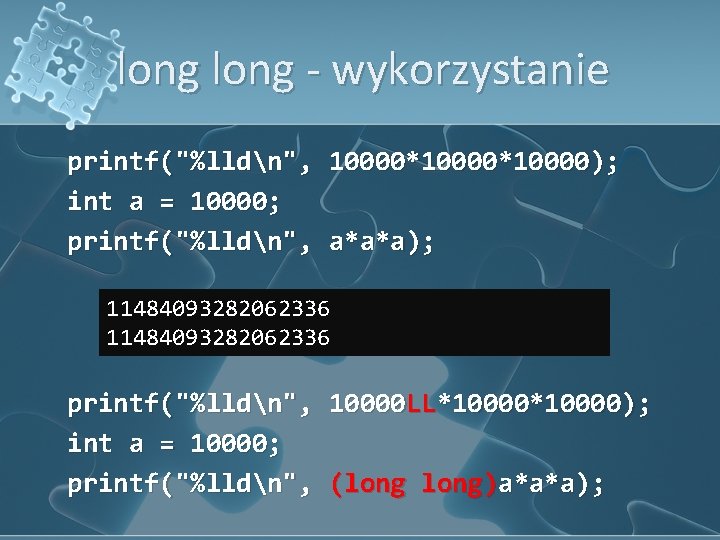
long - wykorzystanie printf("%lldn", 10000*10000); int a = 10000; printf("%lldn", a*a*a); 11484093282062336 printf("%lldn", 10000 LL*10000); int a = 10000; printf("%lldn", (long)a*a*a);

Zadania l Obowiązkowe: 74 l 569 l l Dodatkowe: 438 (łatwe) l 601 (łatwe) l 8998 (średnie) l 2097 (średnie) l 5451 (średnie) l 575 (trudne) l 4580 (trudne, wyszukiwanie binarne) l 3871 (trudne) l