VY32INOVACERONE16 Rovnice a nerovnice Kvadratick nerovnice Zkladn pojmy

VY_32_INOVACE_RONE_16 Rovnice a nerovnice Kvadratické nerovnice

Základní pojmy Kvadratickou nerovnicí s proměnnou x nazýváme všechny nerovnice, které lze zapsat v tvaru ax 2 + bx + c 0 a ϵ R-, b ϵ R kvadratický člen lineární člen absolutní člen ax 2 + bx + c 0

Ekvivalentní úpravy nerovnic 1. Záměna stran nerovnice L(x) P(x) 2. Přičtení stejného čísla nebo výrazu k oběma stranám nerovnice(který je definován v celém oboru řešení nerovnice) 3. Vynásobení obou stran rovnice stejným kladným číslem 4. Při násobení nebo dělení obou stran nerovnice záporným číslem se mění znak nerovnosti na opačný. 5. Umocnění obou nezáporných stran nerovnice

Základní pojmy ŘEŠENÍ KVADRATICKÉ NEROVNICE ax 2 + bx + c 0 Je závislé na DEFINIČNÍM OBORU NEROVNICE Řešením - OBOREM PRAVDIVOSTI NEROVNICE může být množina prvků např. K = {1; 2; 3 } intervaly např. x 3 K = 3; nemá řešení např. 0 3 K={ } OBOR PRAVDIVOSTI NEROVNICE K je číselná množina, která osahuje všechny kořeny nerovnice

Řešení kvadratických nerovnic Při řešení kvadratické nerovnice Ø Rozložíme kvadratický trojčlen na součin Ø součinový tvar řešíme Ø Diskusí ax 2 + bx + c =a. ( x − x 1 ). ( x − x 2 ) +. +=+; -. +=-; -. -=+ Ø metodou intervalů – nulové body jsou kořeny Ø Nalezneme průnik řešení a definovaného intervalu

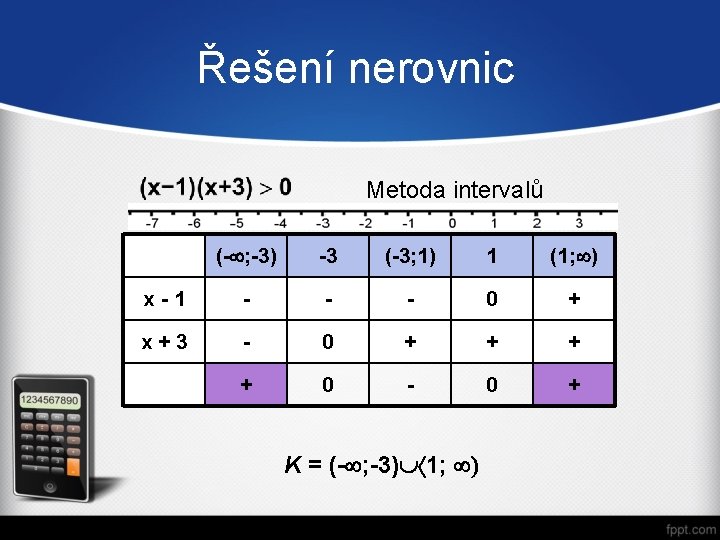
Příklad 1 Řešte nerovnici s neznámou x v R -3 x 2 - 6 x +9 0 : (-3) x 2 + 2 x – 3 0 -3 x 2 +9 6 x Dělíme záporným číslem, znak nerovnosti se mění na opačný zapíšeme součinový tvar

Řešení nerovnic Metoda intervalů (- ; -3) -3 (-3; 1) 1 (1; ) x-1 - - - 0 + x+3 - 0 + + 0 - 0 + K = (- ; -3) 1;

Úlohy k procvičení Řešte nerovnice s neznámou x v množině R 3 x 2 7 – (x-1) 2 3 x + 10 x + 6 8 – (2 x – 1)2 (3 x – 1)2 – 5 x(x – 1) > 4

Příklad 2 Řešte nerovnici s neznámou x v množině R x 2 + 3 + x > x - 2 x 2 + 5 > 0 D = 0 – 4. 5 = - 20 0 pro x = 5 Kořeny nelze najít 52 + 5 = +30 >0 (-5)2 + 5 = +30 >0 K=R

Zdroje • • VOŠICKÝ, Zdeněk. Matematika v kostce. 1. vyd. Havlíčkův Brod: Fragment, 1996, 124 s. ISBN 80 -720 -0012 -8. HUDCOVÁ. Sbírka úloh z matematiky pro SOŠ, studijní obory SOU a nástavbové studium. PROMETHEUS, spol. s r. o. ISBN 10348405. ČERMÁK, Pavel. Odmaturuj! z matematiky. Vyd. 2. (opr. ). Brno: Didaktis, 2003, 208 s. ISBN 80 -862 -8597 -9. http: //www. ucebnice. krynicky. cz/Matematika © RNDr. Anna Káčerová