Univariate Functions Copulas Conditioning with Copulas n Let

Univariate Functions Copulas Conditioning with Copulas n Let C 1(u, v) denote the first partial derivative of C(u, v). F(x, y) = C(FX(x), FY(y)), distribution of Y|X=x is given by: n FY|X(y) = C 1(FX(x), FY(y)) n C(u, v) = uv, the conditional distribution of V given that U=u is C 1(u, v) = v = Pr(V<v|U=u). n If C 1 is simple enough to invert algebraically, then the simulation of joint probabilities can be done using the derived conditional distribution. That is, first simulate a value of U, then simulate a value of V from C 1. Gary G Venter

Univariate Functions Copulas Tails of Copulas ASTIN 2001 Gary G Venter

Univariate Functions Copulas Kendall correlation n t is a constant of the copula n t = 4 E[C(u, v)] – 1 n t = 2 d. E[C(u 1, . . . , ud)] – 1 2 d – 1 Gary G Venter

Univariate Functions Copulas Frank’s Copula n n n n Define gz = e-az – 1 Frank’s copula with parameter a 0 can be expressed as: C(u, v) = -a-1 ln[1 + gugv/g 1] C 1(u, v) = [gugv+gv]/[gugv+g 1] c(u, v) = -ag 1(1+gu+v)/(gugv+g 1)2 t(a) = 1 – 4/a + 4/a 2 0 a t/(et-1) dt For a<0 this will give negative values of t. v = C 1 -1(p|u) = -a-1 ln{1+pg 1/[1+gu(1–p)]} Gary G Venter

Copulas Gary G Venter Univariate Functions

Univariate Functions Copulas Gumbel Copula n C(u, v) = exp{- [(- ln u)a + (- ln v)a]1/a}, a 1. n C 1(u, v) = C(u, v)[(- ln u)a + (- ln v)a]-1+1/a(-ln u)a-1/u n c(u, v) = C(u, v)u-1 v-1[(-ln u)a +(-ln v)a]-2+2/a[(ln u)(ln v)]a-1 {1+(a-1)[(-ln u)a +(-ln v)a]-1/a} n t(a) = 1 – 1/a n Simulate two independent uniform deviates u and v n Solve numerically for s>0 with ues = 1 + as n The pair [exp(-sva), exp(-s(1 -v)a)] will have the Gumbel copula distribution Gary G Venter

Copulas Gary G Venter Univariate Functions

Univariate Functions Copulas Heavy Right Tail Copula n n n C(u, v) = u + v – 1 + [(1 – u)-1/a + (1 – v)-1/a – 1]-a a>0 C 1(u, v) = 1 – [(1 – u)-1/a + (1 – v)-1/a – 1] -a-1(1 – u)-1 -1/a c(u, v) = (1+1/a)[(1–u)-1/a +(1– v)-1/a – 1] -a-2[(1–u)(1–v)]-1 -1/a t(a) = 1/(2 a + 1) Can solve conditional distribution for v Gary G Venter

Copulas Gary G Venter Univariate Functions

Univariate Functions Copulas Joint Burr n F(x) = 1 – (1 + (x/b)p)-a and G(y) = 1 – (1 + (y/d)q)-a n F(x, y) = 1 – (1 + (x/b)p)-a – (1 + (y/d)q)-a + [1 + (x/b)p + (y/d)q]-a n The conditional distribution of y|X=x is also Burr: n FY|X(y|x) = 1 – [1 + (y/dx)q]-(a+1), where dx = d[1 + (x/b)p/q] Gary G Venter

Copulas Univariate Functions Partial Perfect Correlation Copula Generator n n n Assume logical values 0 and 1 are arithmetic also h : unit square unit interval H(x) = 0 xh(t)dt C(u, v) = uv – H(u)H(v) + H(1)H(min(u, v)) C 1(u, v) = v – h(u)H(v) + H(1)h(u)(v>u) c(u, v) = 1 – h(u)h(v) + H(1)h(u)(u=v) Gary G Venter

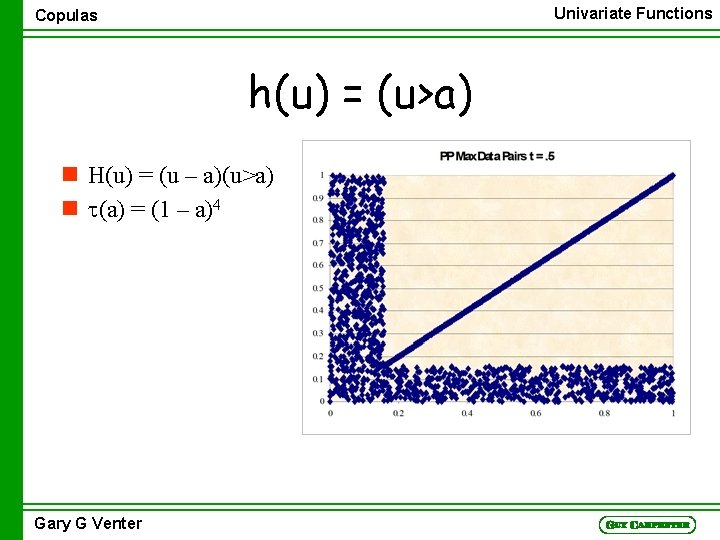
Univariate Functions Copulas h(u) = (u>a) n H(u) = (u – a)(u>a) n t(a) = (1 – a)4 Gary G Venter

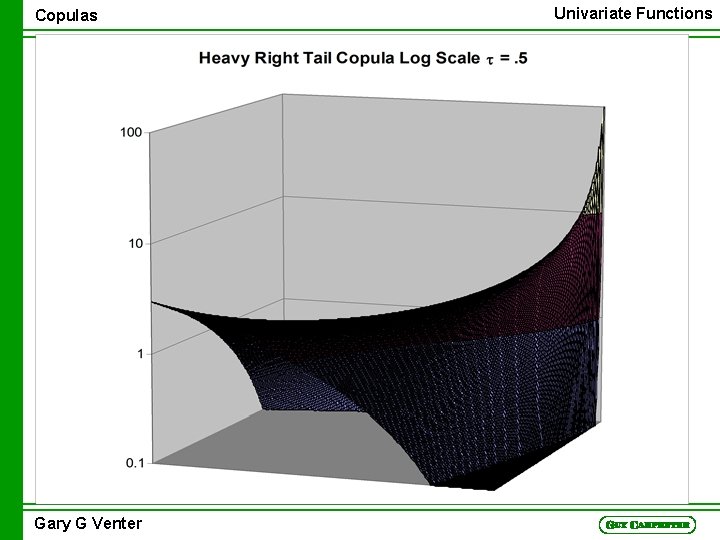
Univariate Functions Copulas h(u) = n H(u) = ua+1/(a+1) n t(a) = 1/[3(a+1)4] + 8/[(a+1)(a+2)2(a+3)] Gary G Venter a u

Copulas Univariate Functions The Normal Copula n n n n n N(x) = N(x; 0, 1) B(x, y; a) = bivariate normal distribution function, = a Let p(u) be the percentile function for the standard normal: N(p(u)) = u, d. N(p(u))/du = N’(p(u))p’(u) = 1 C(u, v) = B(p(u), p(v); a) C 1(u, v) = N(p(v); ap(u), 1 -a 2) c(u, v) = 1/{(1 -a 2)0. 5 exp([a 2 p(u)2 -2 ap(u)p(v)+a 2 p(v)2]/[2(1 -a 2)])} t(a) = 2 arcsin(a)/p a: 0. 15643 0. 38268 0. 70711 0. 92388 0. 98769 t: 0. 10000 0. 25000 0. 50000 0. 75000 0. 90000 Gary G Venter

Copulas Gary G Venter Univariate Functions

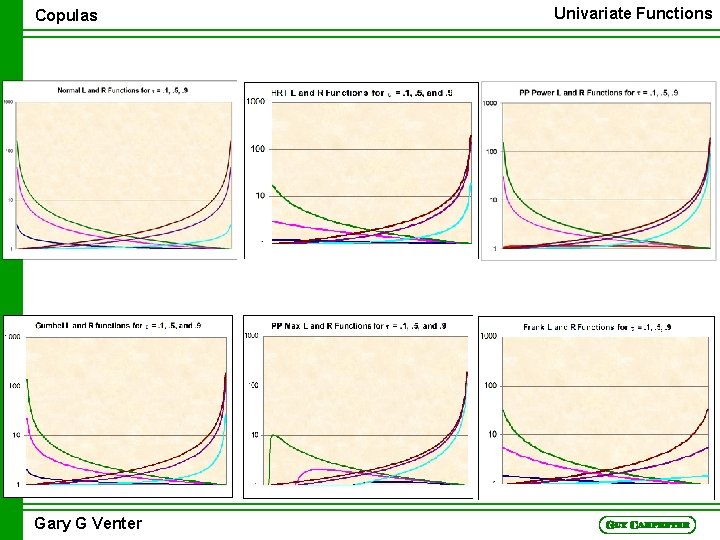
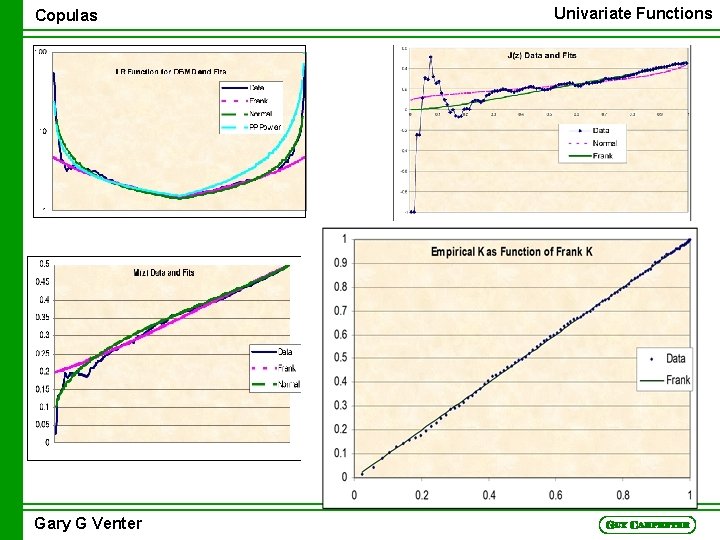
Copulas Univariate Functions Tail Concentration Functions n L(z) = Pr(U<z, V<z)/z 2 n R(z) = Pr(U>z, V>z)/(1 – z)2 n L(z) = C(z, z)/z 2 n 1 - Pr(U>z, V>z) = Pr(U<z) + Pr(V<z) - Pr(U<z, V<z) n = z + z – C(z, z). n Then R(z) = [1 – 2 z +C(z, z)]/(1 – z)2 n Generalizes to multi-variate case Gary G Venter

Copulas Gary G Venter Univariate Functions

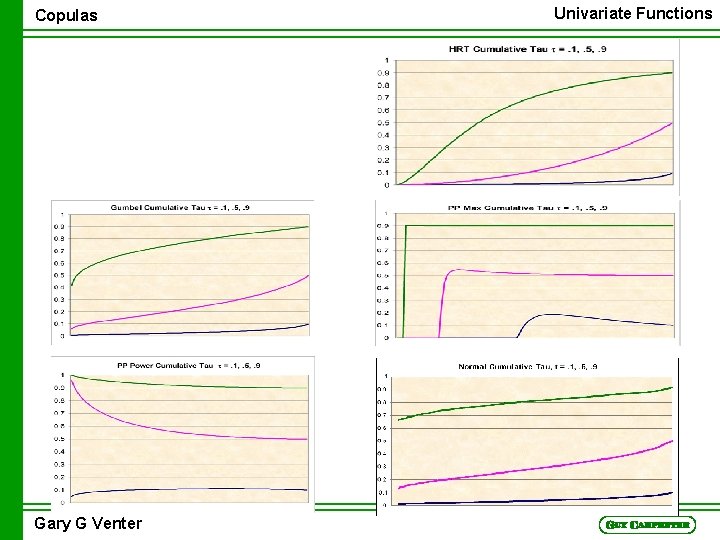
Univariate Functions Copulas Cumulative Tau n t = – 1+4 01 01 C(u, v)c(u, v)dvdu n J(z) = – 1+4 0 z 0 z C(u, v)c(u, v)dvdu/C(z, z)2 n Generalizes to multi-variate case Gary G Venter

Copulas Gary G Venter Univariate Functions

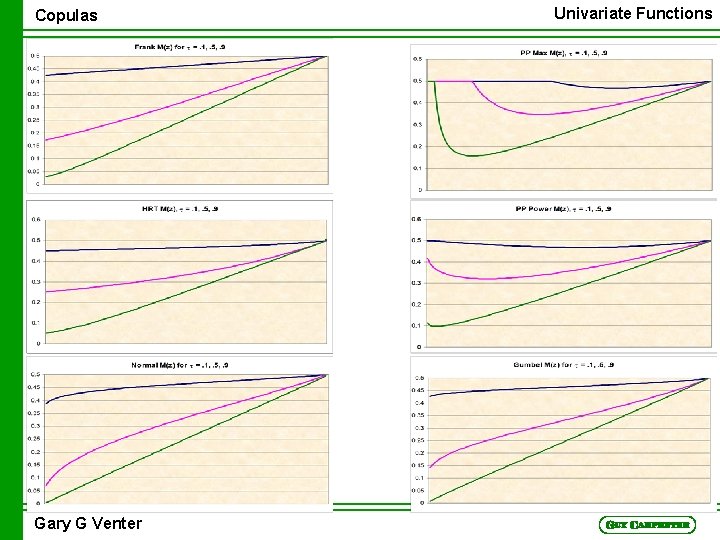
Copulas Univariate Functions Cumulative Conditional Mean n M(z) = E(V|U<z) = z-1 0 z 01 vc(u, v)dvdu n M(1) = ½ n A pairwise concept Copula Distribution Function n K(z) = Pr(C(u, v)<z) n Generalizes to multi-variate case Gary G Venter

Copulas Gary G Venter Univariate Functions

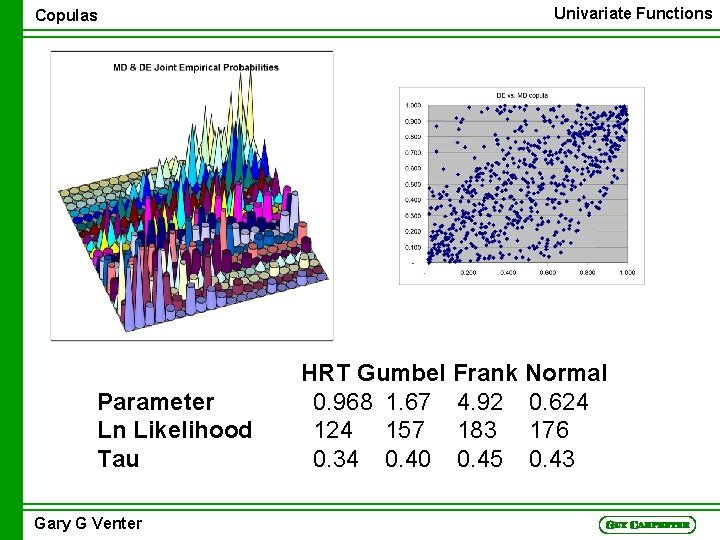
Copulas Parameter Ln Likelihood Tau Gary G Venter Univariate Functions HRT Gumbel Frank Normal 0. 968 1. 67 4. 92 0. 624 157 183 176 0. 34 0. 40 0. 45 0. 43

Copulas Gary G Venter Univariate Functions