TwoDimensional Rotational Kinematics 8 01 W 09 D



































- Slides: 43

Two-Dimensional Rotational Kinematics 8. 01 W 09 D 1 Young and Freedman: 1. 10 (Vector Products) 9. 1 -9. 6, 10. 5

Announcements No Math Review Night Next Week Pset 8 Due Nov 1 at 9 pm, just 3 problems W 09 D 2 Reading Assignment Young and Freedman: 1. 10 (Vector Product) 10. 1 -10. 2, 10. 5 -10. 6 ; 11. 1 -11. 3

Rigid Bodies A rigid body is an extended object in which the distance between any two points in the object is constant in time. Springs or human bodies are non-rigid bodies.

Demo Center of Mass and Rotational Motion of Baton

Overview: Rotation and Translation of Rigid Body Demonstration: Motion of a thrown baton Translational motion: external force of gravity acts on center of mass Rotational Motion: object rotates about center of mass

Recall: Translational Motion of the Center of Mass Total momentum of system of particles External force and acceleration of center of mass

Main Idea: Rotational Motion about Center of Mass Torque produces angular acceleration about center of mass is the moment of inertial about the center of mass is the angular acceleration about center of mass

Two-Dimensional Rotational Motion Fixed Axis Rotation: Disc is rotating about axis passing through the center of the disc and is perpendicular to the plane of the disc. Motion Where the Axis Translates: For straight line motion, bicycle wheel rotates about fixed direction and center of mass is translating

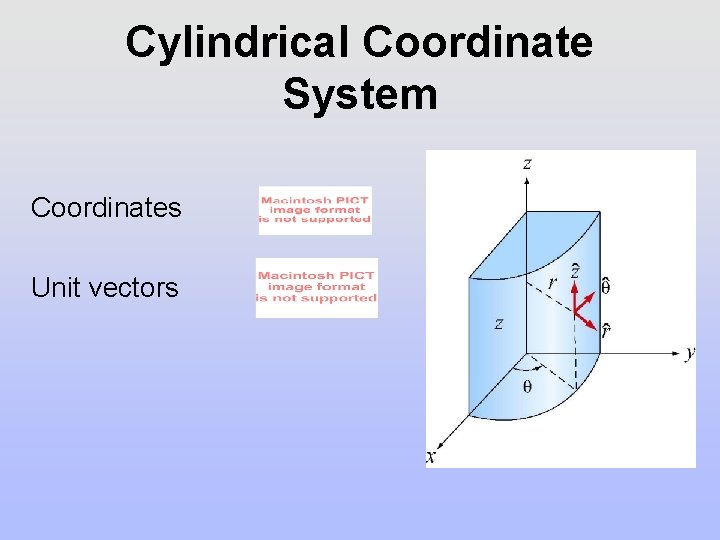
Cylindrical Coordinate System Coordinates Unit vectors

Rotational Kinematics for Point-Like Particle

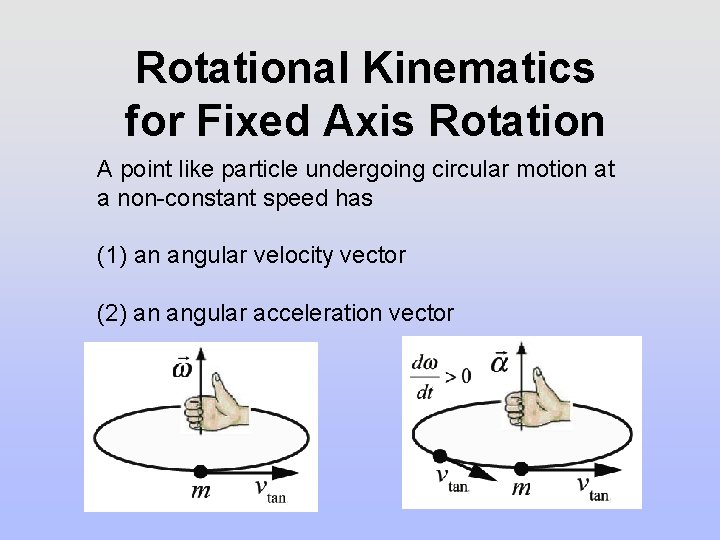
Rotational Kinematics for Fixed Axis Rotation A point like particle undergoing circular motion at a non-constant speed has (1) an angular velocity vector (2) an angular acceleration vector

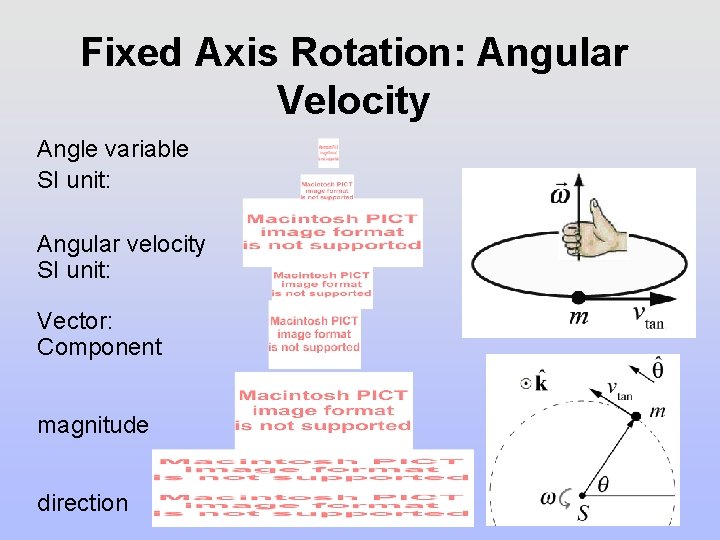
Fixed Axis Rotation: Angular Velocity Angle variable SI unit: Angular velocity SI unit: Vector: Component magnitude direction

Concept Question: Angular Speed Object A sits at the outer edge (rim) of a merry-go-round, and object B sits halfway between the rim and the axis of rotation. The merry-go-round makes a complete revolution once every thirty seconds. The magnitude of the angular velocity of Object B is 1. 2. 3. 4. half the magnitude of the angular velocity of Object A. the same as the magnitude of the angular velocity of Object A. twice the magnitude of the angular velocity of Object A. impossible to determine.

Concept Question: Angular Speed Object A sits at the outer edge (rim) of a merry-go-round, and object B sits halfway between the rim and the axis of rotation. The merry-go-round makes a complete revolution once every thirty seconds. The magnitude of the angular velocity of Object B is • Answer: 2. All points in a rigid body rotate with the same angular velocity.

Example: Angular Velocity Consider point-like object rotating with velocity tangent to the circle of radius r as shown in the figure below with The angular velocity vector points in the given by direction,

Fixed Axis Rotation: Angular Acceleration Angular acceleration: SI unit Vector: Component: Magnitude: Direction:

Rotational Kinematics: Integral Relations The angular quantities are exactly analogous to the quantities for one-dimensional motion, and obey the same type of integral relations Example: Constant angular acceleration

Concept Question: Rotational Kinematics The figure shows a graph of ωz and αz versus time for a particular rotating body. During which time intervals is the rotation slowing down? 1. 0 < t < 2 s 2. 2 s < t < 4 s 3. 4 s < t < 6 s 4. None of the intervals. 5. Two of the intervals. 6. Three of the intervals.

Concept Question: Rotational Kinematics The figure shows a graph of ωz and αz versus time for a particular rotating body. During which time intervals is the rotation slowing down? 1. 0 < t < 2 s 2. 2 s < t < 4 s 3. 4 s < t < 6 s 4. None of the intervals. 5. Two of the intervals. 6. Three of the intervals.

Table Problem: Rotational Kinematics A turntable is a uniform disc of mass m and a radius R. The turntable is initially spinning clockwise when looked down on from above at a constant frequency f. The motor is turned off and the turntable slows to a stop in t seconds with constant angular deceleration. a) What is the direction and magnitude of the initial angular velocity of the turntable? b) What is the direction and magnitude of the angular acceleration of the turntable? c) What is the total angle in radians that the turntable spins while slowing down?

Summary: Circular Motion for Point-like Particle Use plane polar coordinates: circle of radius r Unit vectors are functions of time because direction changes Position Velocity Acceleration

Rigid Body Kinematics for Fixed Axis Rotation Kinetic Energy and Moment of Inertia

Rigid Body Kinematics for Fixed Axis Rotation Body rotates with angular velocity acceleration and angular

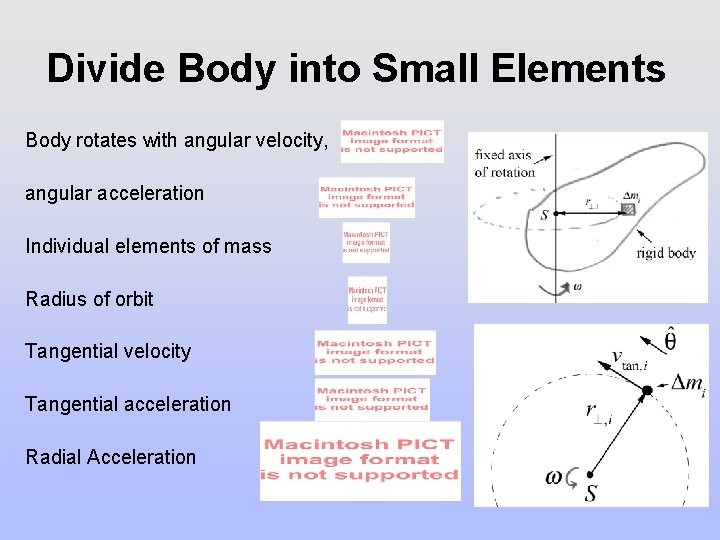
Divide Body into Small Elements Body rotates with angular velocity, angular acceleration Individual elements of mass Radius of orbit Tangential velocity Tangential acceleration Radial Acceleration

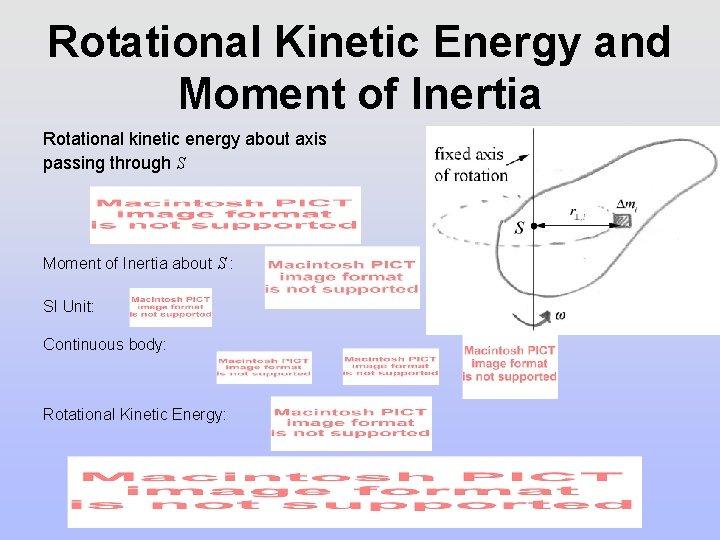
Rotational Kinetic Energy and Moment of Inertia Rotational kinetic energy about axis passing through S Moment of Inertia about S : SI Unit: Continuous body: Rotational Kinetic Energy:

Discussion: Moment of Inertia How does moment of inertia compare to the total mass and the center of mass? Different measures of the distribution of the mass. Total mass: scalar Center of Mass: vector (three components) Moment of Inertia about axis passing through S:

Concept Question All of the objects below have the same mass. Which of the objects has the largest moment of inertia about the axis shown? (1) Hollow Cylinder (2) Solid Cylinder (3)Thin-walled Hollow Cylinder

Concept Question All of the objects below have the same mass. Which of the objects has the largest moment of inertia about the axis shown? Answer 3. The mass distribution for the thin-hollow walled cylinder is furthest from the axis, hence it’s moment of inertia is largest.

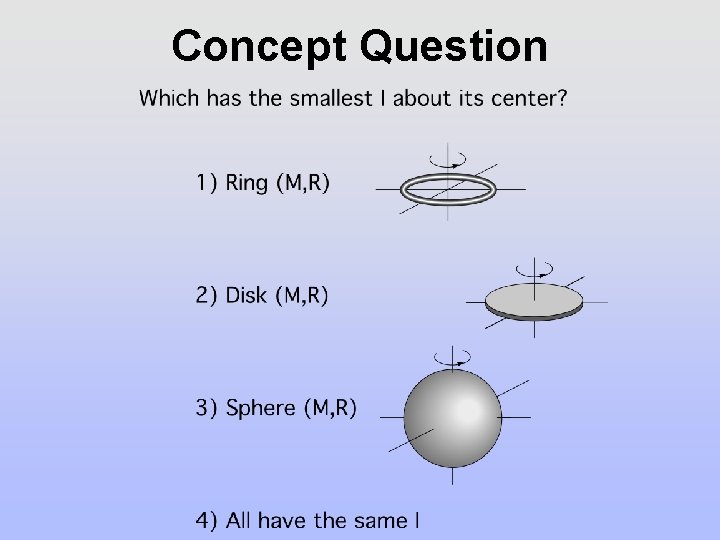
Concept Question

Concept Question Answer 3. The mass of the sphere is on average closer to an axis of rotation passing through its center then in the case of the ring or the disc

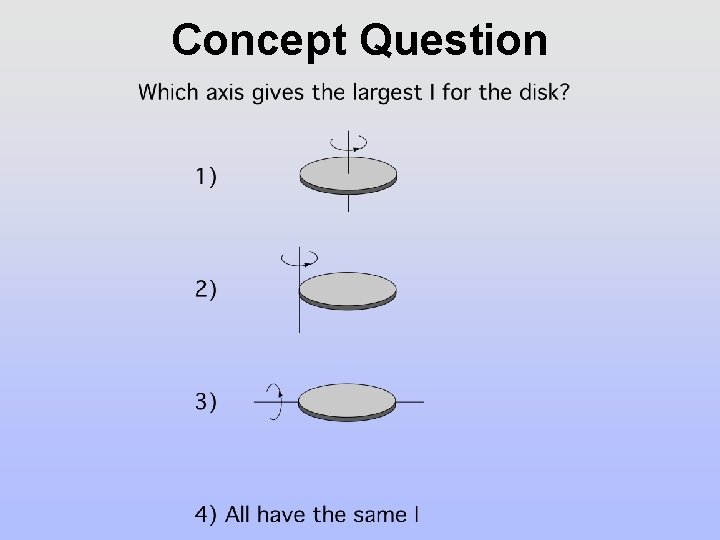
Concept Question

Concept Question Answer 2. The mass of the ring is furthest on average from an axis passing perpendicular to the plane of the disc and passing through a point on the edge of the disc.

Worked Example: Moment of Inertia for Uniform Disc Consider a thin uniform disc of radius R and mass m. What is the moment of inertia about an axis that pass perpendicular through the center of the disc?

Strategy: Calculating Moment of Inertia Step 1: Identify the axis of rotation Step 2: Choose a coordinate system Step 3: Identify the infinitesimal mass element dm. Step 4: Identify the radius, , of the circular orbit of the infinitesimal mass element dm. Step 5: Set up the limits for the integral over the body in terms of the physical dimensions of the rigid body. Step 6: Explicitly calculate the integrals.

Worked Example: Moment of Inertia of a Disc Consider a thin uniform disc of radius R and mass m. What is the moment of inertia about an axis that pass perpendicular through the center of the disc?

Parallel Axis Theorem • Rigid body of mass m. • Moment of inertia about axis through center of mass of the body. • Moment of inertia about parallel axis through point S in body. • d. S, cm perpendicular distance between two parallel axes.

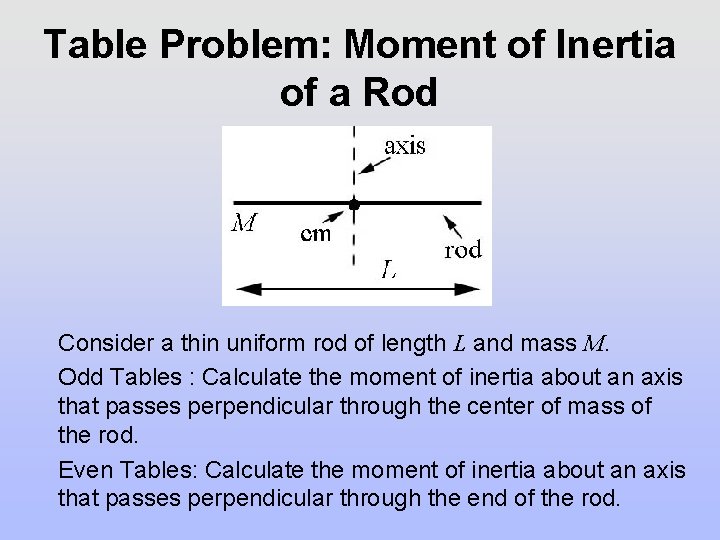
Table Problem: Moment of Inertia of a Rod Consider a thin uniform rod of length L and mass M. Odd Tables : Calculate the moment of inertia about an axis that passes perpendicular through the center of mass of the rod. Even Tables: Calculate the moment of inertia about an axis that passes perpendicular through the end of the rod.

Summary: Moment of Inertia about S: Examples: Let S be the center of mass • rod of length l and mass m • disc of radius R and mass m Parallel Axis theorem:

Table Problem: Kinetic Energy of Disk A disk with mass M and radius R is spinning with angular speed ω about an axis that passes through the rim of the disk perpendicular to its plane. The moment of inertia about the cm is (1/2)M R 2. What is the kinetic energy of the disk?

Concept Question: Kinetic Energy A disk with mass M and radius R is spinning with angular speed ω about an axis that passes through the rim of the disk perpendicular to its plane. Moment of inertia about cm is (1/2)M R 2. Its total kinetic energy is: 1. (1/4)M R 2 ω2 4. (1/4)M Rω2 2. (1/2)M R 2 ω2 5. (1/2)M Rω2 3. 3. (3/4)M R 2 ω2 6. (1/4)M Rω

Concept Question: Kinetic Energy Answer 3. The parallel axis theorem states the moment of inertia about an axis passing perpendicular to the plane of the disc and passing through a point on the edge of the disc is equal to The moment of inertia about an axis passing perpendicular to the plane of the disc and passing through the center of mass of the disc is equal to Therefore The kinetic energy is then

Summary: Fixed Axis Rotation Kinematics Angle variable Angular velocity Angular acceleration Mass element Radius of orbit Moment of inertia Parallel Axis Theorem

Table Problem: Pulley System and Energy Using energy techniques, calculate the speed of block 2 as a function of distance that it moves down the inclined plane using energy techniques. Let IP denote the moment of inertia of the pulley about its center of mass. Assume there are no energy losses due to friction and that the rope does slip around the pulley.
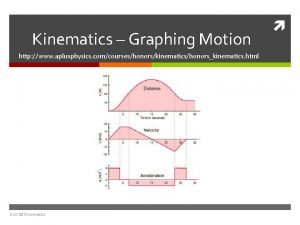
 Aplusphysics kinematics-horizontal kinematics
Aplusphysics kinematics-horizontal kinematics Constant angular acceleration
Constant angular acceleration 4 linear motion equations
4 linear motion equations Angular acceleration
Angular acceleration Angular motion equations
Angular motion equations Magnitude of angular acceleration formula
Magnitude of angular acceleration formula Torque free body diagram
Torque free body diagram Second condition of equilibrium
Second condition of equilibrium Poe practice test answer key
Poe practice test answer key Aplusphysics kinematics-free fall answers
Aplusphysics kinematics-free fall answers Fluid statics ppt
Fluid statics ppt Kinematics physics
Kinematics physics Kinematics ppt free download
Kinematics ppt free download Body kinematics
Body kinematics Kinematics of a particle
Kinematics of a particle Apertura numerica
Apertura numerica Kinematic equations
Kinematic equations Ib physics kinematics
Ib physics kinematics Dh convention
Dh convention Kinematics all formulas
Kinematics all formulas Tricycle kinematics
Tricycle kinematics Rigid body kinetics
Rigid body kinetics Kinematics ppt
Kinematics ppt Describing motion kinematics in one dimension
Describing motion kinematics in one dimension Transport theorem kinematics
Transport theorem kinematics Kinematics
Kinematics Aplusphysics kinematics-defining motion answers
Aplusphysics kinematics-defining motion answers A level physics kinematics
A level physics kinematics Define variable acceleration
Define variable acceleration Holonomic drive
Holonomic drive Kinematics of a particle
Kinematics of a particle Open chain and closed chain kinematics
Open chain and closed chain kinematics Inverse kinematics
Inverse kinematics Rectilinear kinematics continuous motion
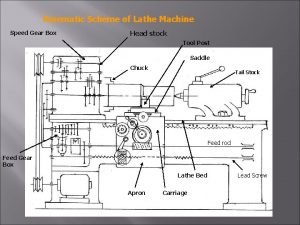
Rectilinear kinematics continuous motion Kinematics of lathe machine
Kinematics of lathe machine Kinematics
Kinematics Kinematics of a particle moving in a straight line
Kinematics of a particle moving in a straight line Kinematics of a particle
Kinematics of a particle Nvvnn
Nvvnn Kinematics of simple harmonic motion
Kinematics of simple harmonic motion Forward kinematics
Forward kinematics Kinematics is the study of
Kinematics is the study of A tourist being chased by an angry bear
A tourist being chased by an angry bear Tempus
Tempus