Tracking J M Sotoca 11 Junio 2002 ndice

Tracking J. M. Sotoca 11 Junio 2002

Índice: 2. 1 Introducción. 2. 2 Obtención de medidas. 2. 2. 1 Modelos de Background. 2. 2. 2 Métodos de medida. 2. 2. 3 Modelos de personas. 2. 2. 4 Integración de modelos. 2. 3 Estimación de estados para sistemas lineales. 2. 3. 1 Conceptos básicos. 2. 3. 2 Estimadores lineales. Caso estático. 2. 3. 3 Filtro de kalman. 2. 3. 4 Modelos cinemáticos. 2. 4 Modelos dinámicos no lineales. 2. 4. 1 Filtro de kalman extendido. 2. 4. 2 Filtro de partículas. 2. 4. 3 Condensation. 2

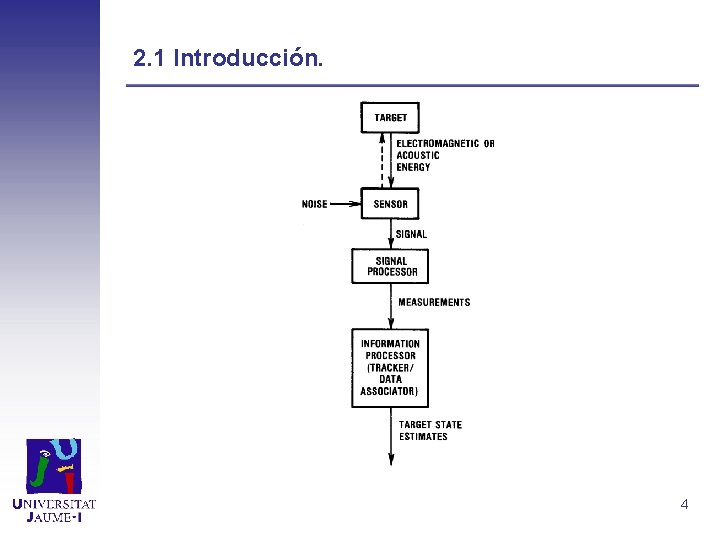
2. 1 Introducción. Mediante el uso de Tracking se busca el estudio y seguimiento mediante estimaciones del estado o blanco (target). Típicamente, se usa en tratamiento de señales y consiste en: Componentes cinemáticas (posición, velocidad, aceleración, etc. . ) Otras componentes (valores de la señal y del espectro asociado, información. . . ) Variación de parámetros ( coeficientes de acoplamiento, velocidad de propagación. . . ) Por medida, entendemos las observaciones con ruido que realizamos sobre el estado actual y pueden ser: Estudio de la posición. Rango y relaciones con el sensor. Tiempo de diferencia de un dato correlacionado entre dos sensores. Frecuencia de banda de la señal emitida en ese estado. Diferencia de frecuencia (efecto doppler) entre dos sensores. Potencia de la señal. 3

2. 1 Introducción. 4

2. 1 Introducción. Dificultad en la asociación de datos durante el proceso de medida, cuestión que genera incertidumbre: Falsas alarmas aleatorias durante la detección del proceso. Confusión debida a reflexiones o radiaciones espúreas cerca del target a medir. Interferencias entre targets. Errores en el proceso de medida. Los problemas de asociación de datos son categorizados de acuerdo a los tipos de asociación: Medición - Medición (inicialización del track). Medición - Track (el objetivo es mantener el track). Track - Track (Fusión entre seguimientos o Track fusion). Modelos de asociación de datos: El estado inicial es conocido o asumido por conveniencia y se escoge en la asociación de datos que más se repite aunque no necesariamente sea la correcta. Se establece una hipótesis de comprobación de datos, asumiendo que esta hipótesis está sujeto a una probabilidad de error y considerando la 5 predicción como si fuera cierta.

2. 1 Introducción En el caso de visión artificial, se busca un conjunto de objetos dado una secuencia de imágenes. Aplicaciones: Captura de movimiento: Si seguimos con precisión el movimiento de personas, podemos hacer un registro de sus trayectorias. Reconocimiento y interpretación: Si el movimiento del objeto es característico podemos identificar los objetos e interpretar la escena. Vigilancia: Detección de actividad de objetos conocidos. Predicción: Dado un conocimiento a priori del movimiento predecir futuras posiciones. 6

2. 1 Introducción. Sistema ADVICER. Contexto: La existencia de lugares donde la seguridad es importante: Cajeros de bancos, estaciones de metro, aeropuertos, etc. Objetivo: Detección asistida por ordenador y clasificación de eventos anómalos. A partir de la detección de actividad se establece un diagnóstico de la escena. Se definen las condiciones de alarma al controlador. A partir del acceso a una base de datos de video el sistema aprende a reconocer, clasificando los eventos detectados. 7

Identificación de situación peligrosa en estación de metro. Detección de congestión en entradas de estaciones. Detección y seguimiento de personas. Interfaz del entorno ADVICER 8

2. 1 Introducción. Reconocimiento de gestos para la comunicación humana. Se utilizan modelos de Markov para clasificar movimientos de personas. El método se basa en diferencias de imagen. A partir del cual se calculan estimadores de movimiento (centro, desviación media, intensidad, . . . ) Se determina la región de interés del gesto. 9

http: //www. fb 9 -ti. uni-duisburg. de/mitarbeiter/eickeler. html 10

2. 2 Obtención de medidas. 11 Junio 2002

2. 2. 1 Modelos de Background. Generación de un modelo de fondo en ausencia de objetos en movimiento. El modelo puede no ser estático, por lo que se busca su variabilidad. Ej. Escenas en un parque. Modelo 1: Sea I(x) la intensidad de imagen en el píxel x, F(x) su valor medio en una secuencia y d(x) la desviación típica media. Modelo 2 (W 4, haritaoglu): Sea M(x) el mínimo, N(x) el máximo de un secuencia para el píxel x y D(x) el cambio máximo interframe encontrado. Modelo 3 (Rosales): Se calcula la matriz de covarianza de la distribución de color para el píxel x en N frames, donde I(x, t) es la intensidad y F(x) es la media. Para cada frame medimos la distancia ene le espacio de color: Región: 12

2. 2. 2 Métodos de Medida: Correspondencia entre el objeto entre distintos frames mediante cajas o algún tipo de plantilla que envuelve al objeto. Existencia de ruido sobre todo en escenas de interiores. Ej: Pantallas de ordenador, reflejos sobre cristal, cambios de iluminación, etc. . . Inicialización: Se utiliza una estrategia de fijar una lista con los objetos existente de forma que la aparición o desaparición de un nuevo objeto supone la supervivencia o desaparición de una hipótesis trascurridos varios frames. Correspondencia: Se establece correlación entre el objeto en dos frames consecutivos midiendo una determinada característica: Correspondencia entre los perfiles del objeto (cambios de forma). Intersecciones del área, correspondencia entre niveles de gris. Utilización de curvas activas (Snakes o PDMs). Medida de parámetros de movimiento o trayectoria. (Curvatura, velocidades). 13

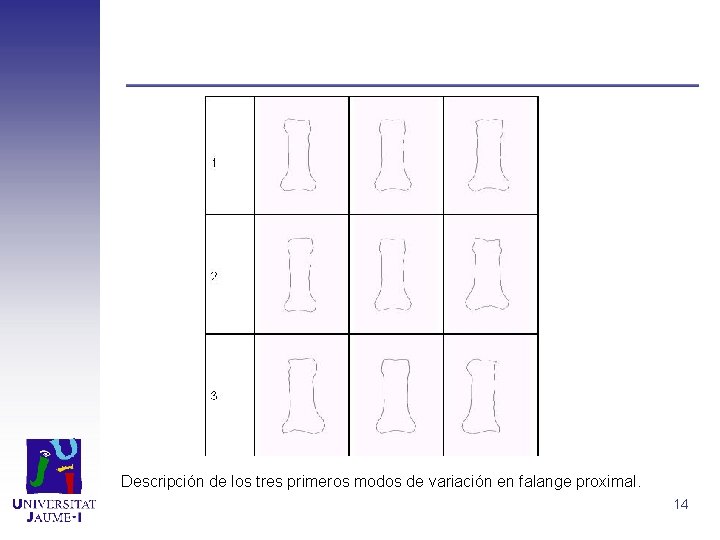
Descripción de los tres primeros modos de variación en falange proximal. 14

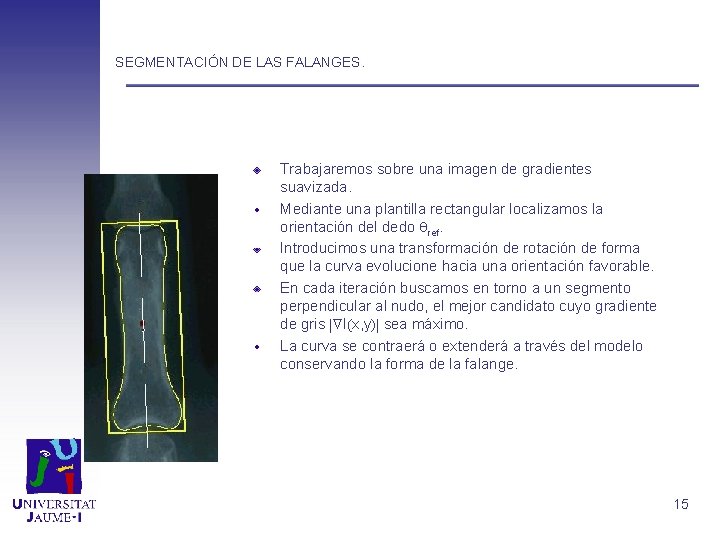
SEGMENTACIÓN DE LAS FALANGES. Trabajaremos sobre una imagen de gradientes suavizada. Mediante una plantilla rectangular localizamos la orientación del dedo ref. Introducimos una transformación de rotación de forma que la curva evolucione hacia una orientación favorable. En cada iteración buscamos en torno a un segmento perpendicular al nudo, el mejor candidato cuyo gradiente de gris I x, y sea máximo. La curva se contraerá o extenderá a través del modelo conservando la forma de la falange. 15

2. 2. 3 Modelos de personas. 16

2. 2. 3 Modelos de personas. 17

2. 2. 4 Integración de modelos (P. Remagnino): Generación de modelos para coches y personas mediante PDM haciendo un PCA. Conocimiento de la geometría de la escena. Calibración de la cámara y obtención de un plano del suelo. Mediante transformaciones proyectar cada objeto sobre el plano suelo. Problema que resuelve: Interacción entre diferentes modelos en la misma escena. Resolución de oclusiones parciales. Estas generan distorsiones en las medidas y perdidas de las características del objeto a seguir. 18

2. 2. 4 Integración de modelos. 19

2. 2. 4 Integración de modelos. 20

2. 3 Estimación de estados para sistemas lineales 11 Junio 2002

2. 3. 1 Conceptos básicos. El problema de estimar un parámetro x es el siguiente. Supongamos que j representa un índice de tiempos discretos y que la medida de observaciones es: son realizadas en presencia de ruido aleatorio w(j). Para cada k medidas encontramos una función estimación: donde Zk es el conjunto de estimaciones del parámetro x en ese instante. Hay dos modelos para parámetros invariantes en el tiempo: No aleatorios, en donde hay un valor verdadero x desconocido. Aleatorios, en donde la variable es aleatoria con una función densidad de probabilidad a priori p(x). En el primer caso buscamos estimar el valor de x cuando k . En el segundo caso, dado una función densidad de probabilidad PDF a priori del parámetro, se puede obtener su correspondiente PDF a posteriori utilizando la regla de bayes: 22

2. 3. 1 Conceptos básicos Sin embargo, si el parámetro es no aleatorio sus funciones PDF a priori y a posteriori no están definidas por lo que solo tenemos la función de probabilidad: Un método de estimación de parámetros no aleatorios es estimar la probabilidad máxima o “maximum likelihood” (ML). La correspondiente estimación aleatoria es la máxima probabilidad a posteriori MAP. Ej: z=x + w. Asumiendo que x es una constante no conocida y w es N(0, 02) tenemos: 23

2. 3. 1 Conceptos básicos La probabilidad a priori en este caso es: Asumiendo que x es independiente de w, la posteriori PDF será: Estimación por mínimos cuadrados: Otro procedimiento de estimación común para parámetros no-aleatorios, son el método de mínimos cuadrados LS. Sea La estimación de x para cada instante k es minimizar la suma de los errores al cuadrado. 24

2. 3. 1 Conceptos básicos. En el caso de parámetros aleatorios, esto supone minimizar el error cuadrático medio MMSE. que supone minimizar la estimación de la varianza cuya solución es la media condicional según los valores sean continuos o discretos. La cualidad de un estimador es medida mediante la varianza. Para un estimador de un parámetro no aleatorio x con valor verdadero x 0, la varianza es para un estimador con parámetro aleatorio x , a varianza es la misma que la expresión anterior sustituyendo x 0 por x. 25

2. 3. 1 Conceptos básicos. Consistencia: Un estimador no aleatorio se dice que es consistente si Eficiencia: De acuerdo con el teorema de baja banda de Cramer-Rao (CRLB), el error cuadrático medio correspondiente al estimador de un parámetro no puede ser más pequeño que una cierta cantidad relacionada con la pdf. J es la información de Fisher y x 0 es el valor verdadero de x. Analogamente para una variable x aleatoria. J se interpreta a veces como la inversa de la matriz de covarianza. 26

2. 3. 2 Estimadores lineales. Caso estático. Consideremos dos variables aleatorias x y z con distribución gaussiana. Sea La notación y matriz de covarianza indica una variable y con medias donde entonces el mínimo error cuadrático medio MMSE del estimador x en términos de z es la media condicional de x dado z, y el correspondiente error condicional de la matriz de covarianza es 27

2. 3. 2 Estimadores lineales. Caso estático. Estimación lineal del mínimo error cuadrático medio: Sean x y z dos variables aleatorias tal que: Consideremos el mejor estimador lineal MMSE En una estimación óptima se espera que: Sustituyendo b, el error de estimación es: Por otro lado, por ortogonalidad: Sustituyendo A en la ecuación llegamos a la ecuación (1). Análogamente, el error de la matriz de covarianza: que corresponde con la ecuación(2). 28

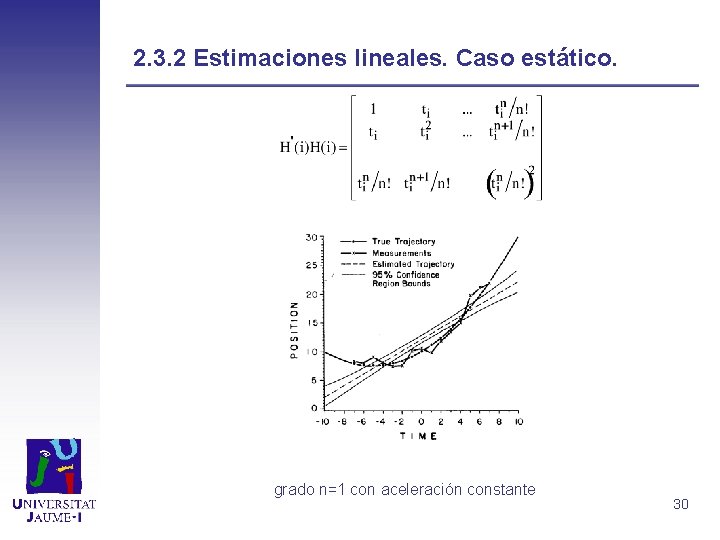
2. 3. 2 Estimadores lineales. Caso estático Ajuste polinómico con ruido en las medidas: Consideremos el siguiente polinomio: donde aj son los parámetros a estimar. Las medidas con ruido en la posición pueden ser descritas por z(i)=H(i)a+w(i), i= 1, . . . , k, donde el vector de parámetros a=(a 0 a 1. . . an) y H(i)=(1 ti ti 2/2!. . . tin /n!). Consideraremos w(i) un ruido no correlacionado con media cero y varianza 2 de acuerdo a la covarianza Rk = 2 I, donde I es la matriz identidad. Por otro lado Combinando ambas expresiones llegamos a la siguiente estimación: 29

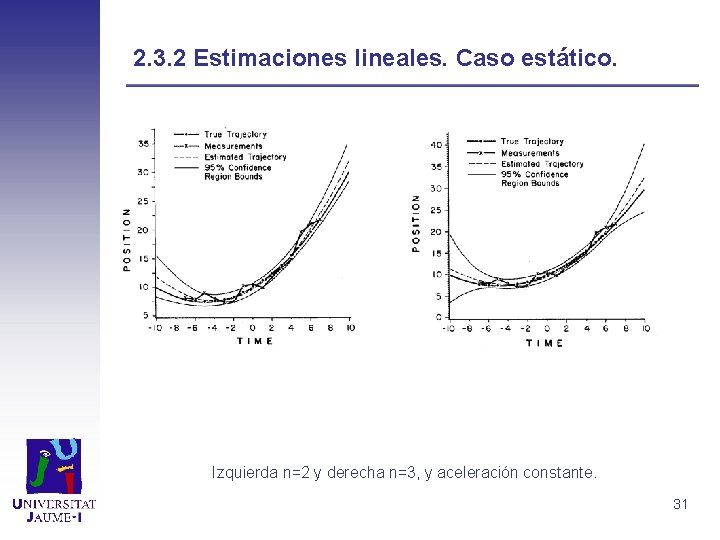
2. 3. 2 Estimaciones lineales. Caso estático. grado n=1 con aceleración constante 30

2. 3. 2 Estimaciones lineales. Caso estático. Izquierda n=2 y derecha n=3, y aceleración constante. 31

2. 3. 3 Filtro de kalman. Sea x(k) el vector de estado en el sistema dinámico en el tiempo k, y u(k) un vector de entradas conocido o control de la señal. La propagación del estado en el tiempo tk+1 puede expresarse como: donde v(k) es un ruido gaussiano de media cero y matriz de covarianza Q(k). Supongamos una serie de observaciones o medidas en el tiempo, cuya ecuación es: donde w(k) es el ruido gaussiano de una secuencia de media cero y matriz de covarianza R(k) y que no esta correlacionado con v(k). El estado inicial es una gaussiana de media x^(0|0) y covarianza P(0|0). En cada paso la estimación es x^(k|k) E(x(k)|Zk), donde Zk={z(j), j =1. . . k) las medidas en función de k. El error condicional asociado al matriz de covarianza es: El filtro de kalman minimiza en el estado de tiempo tk el error condicional asociado a esta matriz de covarianza. 32

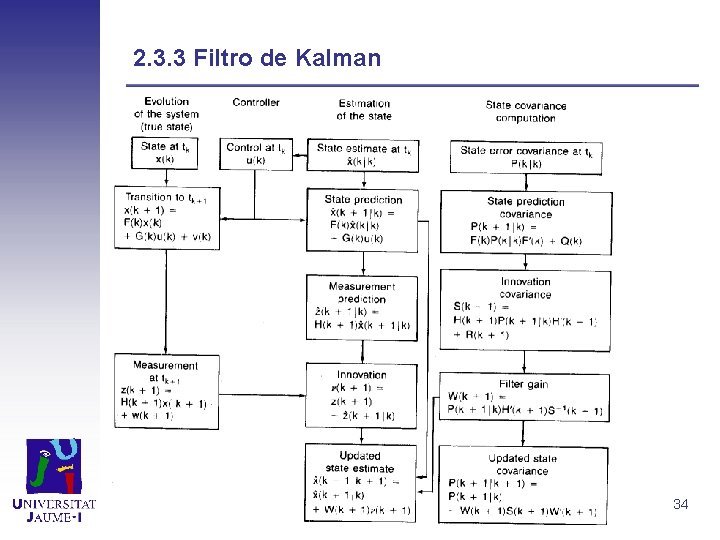
2. 3. 3 Filtro de kalman. State prediction: Measurement prediction: Innovation: State prediction covariance: Innovation covariance: Filter Gain: Updated state estimate: Updated state covariance: 33

2. 3. 3 Filtro de Kalman 34

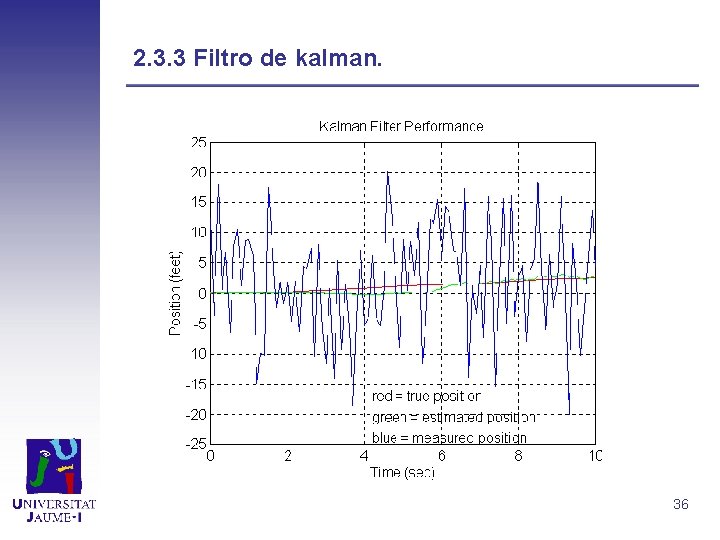
2. 3. 3 Filtro de kalman Ejemplo simulado de filtro de kalman: Ecuación de estado xk+1= Akxk+wk donde wk es un ruido gaussiano. Consideramos como variables la posición y la velocidad. ak es una aceleración aleatoria variable con el tiempo y T es el tiempo entre k y k+1. Supongamos que medimos la posición p a través de la ecuación zk = pk + vk, donde vk es un ruido aleatorio. Sea la aceleración 0. 5 pies/s 2 y que la posición puede variar con un error de 10 pies ( desviación estandar) Tomaremos como parámetros alpha=1, dt =0. 5 y duración 30. Ej: ( código en matlab) www. innovatia. com/software/papers/kalman. htm 35

2. 3. 3 Filtro de kalman. 36

2. 3. 3 Filtro de kalman function kalman(alpha, duration, dt) % alpha = forgetting factor (alpha >= 1) % duration = length of simulation (seconds) % dt = step size (seconds) measnoise = 10; % position measurement noise (feet) accelnoise = 0. 5; % acceleration noise (feet/sec^2) a = [1 dt; 0 1]; % transition matrix c = [1 0]; % measurement matrix x = [0; 0]; % initial state vector xhat = x; % initial state estimate Q = accelnoise^2 * [dt^4/4 dt^3/2; dt^3/2 dt^2]; % process noise covariance P = Q; % initial estimation covariance R = measnoise^2; % measurement error covariance Inn = zeros(size(R)); % set up the size of the innovations vector pos = []; % true position array poshat = []; % estimated position array posmeas = []; % measured position array Counter = 0; % contador de ciclos. 37

2. 3. 3 Filtro de kalman for t = 0 : dt: duration, Counter = Counter + 1; Process. Noise = accelnoise * [(dt^2/2)*randn; dt*randn]; % Simulate the process x = a * x + Process. Noise; Meas. Noise = measnoise * randn; % Simulate the measurement z = c * x + Meas. Noise; Inn = z - c * xhat; % Innovation s = c * P * c' + R; % Covariance of Innovation K = a * P * c' * inv(s); % Gain matrix xhat = a * xhat + K * Inn; % State estimate P = a * P * a' + Q - a * P * c' * inv(s) * c * P * a'; % Covariance of prediction error % Save some parameters in vectors for plotting later pos = [pos; x(1)]; posmeas = [posmeas; z]; poshat = [poshat; xhat(1)]; end % Plot the results t = 0 : dt : duration; t = t'; plot(t, pos, 'r', t, poshat, 'g', t, posmeas, 'b'); grid; xlabel('Time (sec)'); ylabel('Position (feet)'); title('Kalman Filter Performance'); 38

2. 3. 4 Modelos cinemáticos Modelo con velocidad constante: Consideraremos la aceleración nula x’’(t)=0. En la practica, la velocidad puede tener pequeños cambios debidos a ruido x’’(t)= (t). El vector de estado será: La velocidad vendrá dada por: donde La ecuación para tiempos discretos con intervalo T es: donde El proceso de ruido puede expresarse de la siguiente forma: La covarianza de v(k) asumiendo E[ (t)]=q (t- ) será: 39

2. 3. 4 Modelos cinemáticos Modelo con aceleración constante: Filtro - - : 40

2. 4. 1 Filtro de kalman extendido (EKF). Consideremos un sistema con ecuación dinámica: donde E[v(k)]=0, y E[v(k)v’(k)]=Q(k) kj. La medida es: donde E[w(k)]=0, y E[w(k)w’(k)]=R(k) kj. Asumimos que el proceso y la medida del ruido no están correlacionados. En el caso lineal asumimos que: donde tendrá asociada una covarianza P(k|k). Para obtener la predición del estado en el estado k+1 para el caso no lineal, se desarrolla en series de Taylor en primer y segundo orden, obteniendo la siguiente expresión: donde ei es un vector base en coordenadas cartesianas. Eliminando términos altos, e introduciendo la matriz de covarianza P llegamos a la siguiente formulación: 41

2. 4. 1 Filtro de kalman extendido (EKF). Análogamente, puede obtenerse una expresión para la estimación de la covarianza: En el caso de la predición de la medida para un filtro hasta segundas derivadas tenemos: Y su correspondiente covarianza asociada sería: Si comparamos con el caso lineal para el filtro de kalman, fx(k) hace el papel de la función F(k) y hx(k+1) hace el papel de la función H(k+1). 42

2. 4. 2. Filtro de partículas. Caso general: 43

2. 4. 2. Filtro de partículas. 44

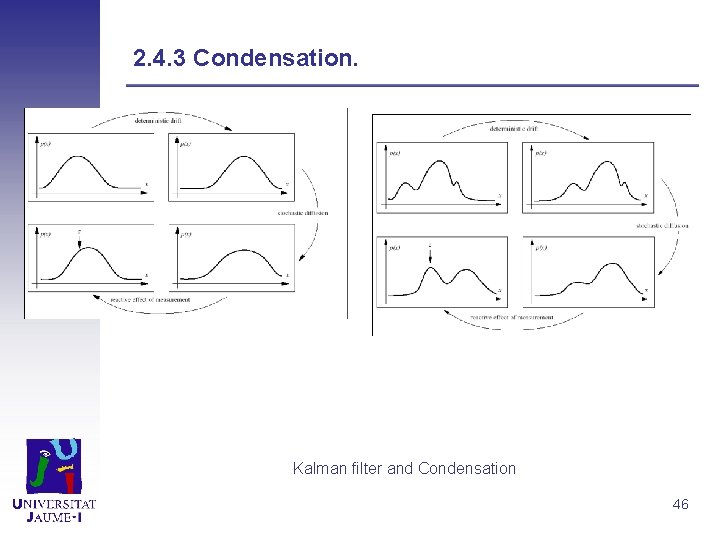
2. 4. 3 Condensation. Se busca poder realizar estimaciones para propagaciones de densidad de probabilidad no gaussiana. Para ello generamos un conjunto de muestras s={s(1), . . . , s(N)} con probabilidades a priori ={ (1), . . . , (N)} y probabilidades acumuladas c={c(1), . . . , c(N)}. Las muestras son generadas aleatoriamente con distribución uniforme. La función de estimación de la certeza de la medida p(z|x) suele ser la desviación respecto a una gaussiana centrada en la media de la población en el caso de seguir un solo objeto. El sistema es aplicable al seguimiento de multiobjetos, si el criterio de medida es lo suficientemente general para detectar la existencia de los mismos. En ese caso se puede aplicar el teorema de bayes para obtener las probabilidades a posteriori de los pesos. La principal ventaja de esta técnica es que utiliza la distribución de probabilidad acumulada para decidir que muestras van a sobrevivir en cada iteración, concentrándose los pesos con mayor probabilidad en aquellas hipótesis que obtienen una mejor medida. 45

2. 4. 3 Condensation. Kalman filter and Condensation 46

2. 4. 3 Condensation. 47

2. 4. 3 Condensation. 48