Timed IO Automata A Mathematical Framework for Modeling






















- Slides: 25

Timed I/O Automata: A Mathematical Framework for Modeling and Analyzing Real-Time Systems Frits Vaandrager, University of Nijmegen joint work with Dilsun Kaynar and Nancy Lynch, MIT Roberto Segala, University of Verona FV supported by EU IST project AMETIST

Objectives A mathematical framework for modeling and analyzing real-time systems Focus on expressiveness rather than on automatic verification System designers can use this framework for Decomposition of complex system descriptions into manageable pieces Description at multiple levels of abstraction Statement and proof of safety, liveness and performance properties

Contributions Improved formal model for real-time systems Interesting special case of hybrid I/O automata Simplified treatment of receptivity “The problem with timed automata is that if you compose them you get deadlocks” (George Logothetis, RTSS 03)

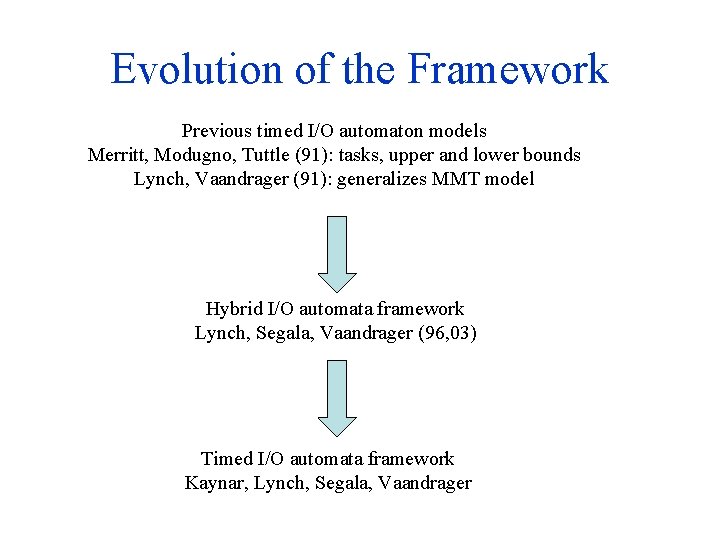
Evolution of the Framework Previous timed I/O automaton models Merritt, Modugno, Tuttle (91): tasks, upper and lower bounds Lynch, Vaandrager (91): generalizes MMT model Hybrid I/O automata framework Lynch, Segala, Vaandrager (96, 03) Timed I/O automata framework Kaynar, Lynch, Segala, Vaandrager

Describing Timed Behavior Variable v Static type, type(v) Dynamic type, dtype(v): allowed “trajectories” for v Functions from time intervals to type(v) Valuation for V: assigns value in type(v) to each v in V Trajectory Models evolution of variables over time interval I I-trajectory for V: maps I to valuations for V; restriction to each v is in dtype(v) Hybrid sequence Models a series of discrete and continuous changes 0 a 1 1 a 2 2 …, alternating sequence of trajectories and actions I

Timed Automaton (TA) X: internal variables Q: states, a set of valuations of X Θ: start states, a non-empty subset of Q E, H: external, internal actions D Q (E U) Q: discrete transitions T: a set of trajectories for X such that (t) Q for all t in domain( )

Automaton Channel(b, M) where b R+ Variables X: discrete queue (M R)* initially empty analog now R initially 0 States Q: val(X) Actions A: external send(m), receive(m) where m M Transitions D: external send(m) effect add (m, now+b) to queue external receive(m, local u) precondition (m, u) is the first element of queue urgency u = now effect remove first element of queue Trajectories T: satisfies constant(queue) d(now)=1

Automaton Synch(u, )i where u R+, 0 < 1, i I Variables X: discrete nextsend, maxother R initially 0 analog physclock R initially 0 Derived Variables: logclock = max(maxother, physclock) States Q: val(X) Actions A: external send(m)i, receive(m)j, i where m R, j I, j i Transitions D: external send(m)i precondition m=physclock physclock=nextsend urgency true effect nextsend : = nextsend + u external receive(m)j, i effect maxother : = max(maxother, m) Trajectories T: satisfies constant(nextsend), constant(maxother) 1 - d(physclock) 1+

Executions and Traces Execution fragment: Hybrid sequence 0 a 1 1 a 2 2 …, where: Each i is a trajectory of the automaton and Each ( i. lstate, ai+1 , i+1. fstate) is a discrete transition Execution: Execution fragment beginning in a start state Trace: Restrict to external actions and trajectories over empty set of variables

Implementation Relationships A implements B if they have the same external interface and traces(A) traces(B) Simulation relations provide sufficient conditions for showing that one automaton implements another Several types of simulation relations (forward, backward, history, prophecy) have been defined for timed automata

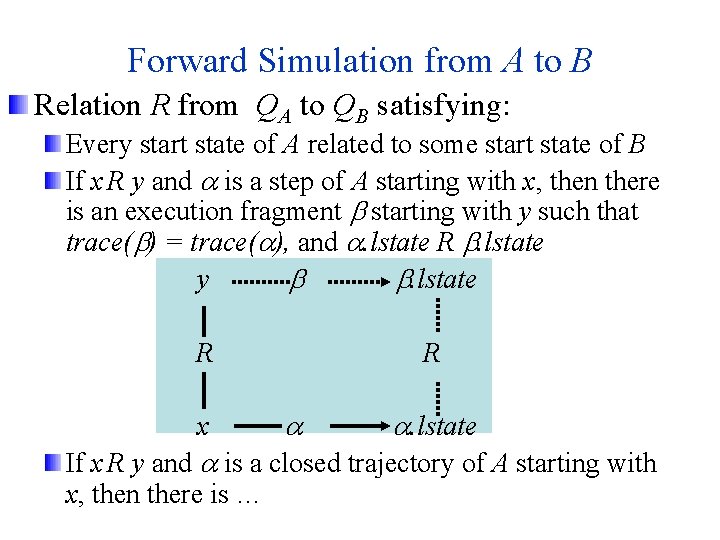
Forward Simulation from A to B Relation R from QA to QB satisfying: Every start state of A related to some start state of B If x R y and is a step of A starting with x, then there is an execution fragment starting with y such that trace( ) = trace( ), and . lstate R . lstate y . lstate R x R . lstate If x R y and is a closed trajectory of A starting with x, then there is …

Simulation Theorems Theorem: If there is a simulation relation from A to B then A implements B.

Example: Simulation Automaton Send. Val(u, )i where u R+, 0 < 1, i I Variables X: discrete counter N initially 0 analog now R initially 0 States Q: val(X) Actions A: external send(m)i, receive(m)j, i where m M, j I, j i Transitions D: external send(m)i precondition m= counter u / (1+ ) now urgency now = counter u / (1 - ) effect counter : = counter + 1 external receive(m)j, i Trajectories T: satisfies constant(counter) d(now)=1

Forward Simulation Relation R Suppose that: x is a state of Synch(u, )i , y is a state of Send. Val(u, )i Then x R y provided that the following conditions hold: y(now) (1 - ) x(physclock) y(now)(1+ ) y(counter) = x(nextsend)/u

Composition Assume A 1 and A 2 are compatible (internal actions are private). Then, A = A 1 || A 2 is the following automaton: X = X 1 X 2 States Q: Projections in Q 1, Q 2 E = (E 1 E 2 ) ; H=(H 1 H 2 ) Start states, discrete steps, trajectories: Projections Projection/pasting theorem: If A = A 1 || A 2 then traces(A) is the set of hybrid sequences (of the right type) whose restrictions to A 1 and A 2 are traces of A 1 and A 2, resp. Substitutivity theorem: If A 1 implements A 2 and both are compatible with B, then A 1 || B implements A 2 || B.

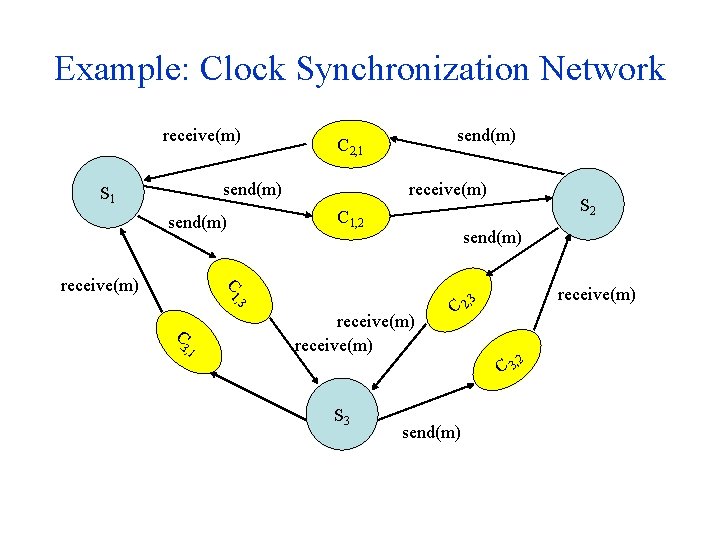
Example: Clock Synchronization Network receive(m) send(m) S 1 receive(m) C 1, 2 send(m) 3, 1 receive(m) 3 , 3 C S 2 send(m) C 1 receive(m) send(m) C 2, 1 receive(m) , C 2 C 3, S 3 send(m) 2

Invariants for Clock Synchronization Network The difference between any physical clock and the real time at time t is at most t The difference between any two physical clock values is at most 2 t (Validity): The logical clock values of all the processes are always between the minimum and the maximum physical clock values in the system All the logical clocks differ from real time at time t by at most t (Agreement): The difference between two logical clocks is always bounded by u + b(1+ )

Timed I/O Automata (TIOA) A TIOA is a TA where the set of external actions is partitioned into inputs and outputs Inputs: model actions of the environment Outputs: model external actions under the system’s control Two additional axioms are required to hold: (Input enabling): A TIOA is able to accommodate an input action whenever it arrives (Time-passage enabling): A TIOA either allows time to advance forever, or it allows time to advance for a while, up to a point where it is prepared to react with some locally controlled action

Example: From TA to TIOA Channel(b, M) can be turned into a TIOA: Classify send actions as inputs Classify receive actions as outputs Synch(u, )i , can be turned into a TIOA: Classify send actions as outputs Classify receive actions as inputs

I/O Feasibility An automaton is I/O feasible if it is capable of providing some response from any state, for any sequence of input actions and any amount of intervening time-passage. A basic requirement for a reasonable TIOA I/O feasibility is not preserved by composition of TIOAs Search for a condition that implies I/O feasibility and is preserved by composition

Progressive TIOAs A TIOA is progressive if it never generates infinitely many locally controlled actions in finite time Theorem: Every progressive TIOA is I/O feasible Theorem: Composition of progressive TIOAs is progressive

Receptive TIOAs But progressiveness is not enough: TIOAs involving only upper bounds on timing are not progressive A strategy for a TIOA A is a TIOA that is the same as A except that it restricts the sets of discrete steps and trajectories TIOA is receptive if it has a progressive strategy Theorem: Every receptive TIOA is I/O feasible Theorem: If A 1 and A 2 are compatible receptive TIOAs with progressive strategies B 1 and B 2, then A 1 || A 2 is receptive with progressive strategy B 1 || B 2

Example: Receptiveness Channel(b, M) is not progressive: Allows an infinite execution in which send and receive actions alternate without any time passage in between Channel(b, M) is receptive: Has a progressive strategy: add condition u=now to precondition of receive so that messages are delivered exactly at their delivery deadline Synch(u, )i is receptive The clock synchronization network is receptive

Related Work Alur-Dill timed automata Uppaal/Kronos/IF/. . . Linear hybrid automata Hytech Work of Sifakis et al on TAs with deadlines Previous I/O automaton based models

Conclusions and Future Work The TIOA framework is a new modeling framework for timed systems Special case of new HIOA model General enough to collect and summarize previous timed I/O automata work Establishes formal relationships with other models Tool development project in progress Extension of the IOA language Automatic translation to UPPAAL More details in monograph Theory of Timed I/O Automata. Available at: http: //theory. lcs. mit. edu/tds/reflist. html
 Helen erickson biography
Helen erickson biography Dimensional modeling vs relational modeling
Dimensional modeling vs relational modeling Complex impedances
Complex impedances Mathematical modeling and engineering problem solving
Mathematical modeling and engineering problem solving Mathematical modeling and engineering problem solving
Mathematical modeling and engineering problem solving Econ213
Econ213 Port mapper failure - timed out
Port mapper failure - timed out Completeness in 7cs of communication
Completeness in 7cs of communication Pastimistic
Pastimistic Off delay timer symbol
Off delay timer symbol Hand up pair up
Hand up pair up Timed essay examples
Timed essay examples Timed writing rubric
Timed writing rubric Timed stands test manual
Timed stands test manual Borra hål för knoppar
Borra hål för knoppar Bris för vuxna
Bris för vuxna Mat för unga idrottare
Mat för unga idrottare Ledarskapsteorier
Ledarskapsteorier Frgar
Frgar Argument för teckenspråk som minoritetsspråk
Argument för teckenspråk som minoritetsspråk Indikation för kejsarsnitt på moderns önskan
Indikation för kejsarsnitt på moderns önskan Datorkunskap för nybörjare
Datorkunskap för nybörjare Ekologiskt fotavtryck
Ekologiskt fotavtryck Rita perspektiv
Rita perspektiv Redogör för vad psykologi är
Redogör för vad psykologi är Lek med geometriska former
Lek med geometriska former