The Real Zeros of a Polynomial Function REMAINDER

The Real Zeros of a Polynomial Function

REMAINDER THEOREM Let f be a polynomial function. If f (x) is divided by x – c, then the remainder is f (c). Let’s look at an example to see how this theorem is useful. So the remainder we get in synthetic division is the same as the answer we’d get if we put -2 in the function. The root of x + 2 = 0 is x = -2 Find f(-2) -2 2 -3 2 -1 -4 14 -32 2 -7 16 -33 using synthetic division let’s divide by x + 2 the remainder

FACTOR THEOREM Let f be a polynomial function. Then x – c is a factor of f (x) if and only if f (c) = 0 If and only if means this will be true either way: 1. If f(c) = 0, then x - c is a factor of f(x) Try synthetic 2. If x - c is a factor of f(x) then f(c) = 0. division and see if the remainder is 0 Opposite -3 -4 5 0 8 NO it’s not a sign goes 12 -51 153 factor. In fact, here -4 17 -51 161 f(-3) = 161 We could have computed f(-3) at first to determine this. Not = 0 so not a factor

Our goal in this section is to learn how we can factor higher degree polynomials. For example we want to factor: We could randomly try some factors and use synthetic division and know by the factor theorem that if the remainder is 0 then we have a factor. We might be trying things all day and not hit a factor so in this section we’ll learn some techniques to help us narrow down the things to try. The first of these is called Descartes Rule of Signs named after a French mathematician that worked in the 1600’s. Rene Descartes 1596 - 1650

Descartes’ Rule of Signs Let f denote a polynomial function written in standard form. The number of positive real zeros of f either equals the number of sign changes of f (x) or else equals that number less an even integer. The number of negative real zeros of f either equals the number of sign changes of f (-x) or else equals that number less an even integer. 1 2 starts Pos. changes Neg. changes Pos. There are 2 sign changes so this means there could be 2 or 0 positive real zeros to the polynomial.

Descartes’Rule of Signs Let f denote a polynomial function written in standard form. The number of positive real zeros of f either equals the number of sign changes of f (x) or else equals that number less an even integer. The number of negative real zeros of f either equals the number of sign changes of f (-x) or else equals that number less an even integer. 1 starts Pos. changes Neg. 2 changes Pos. There simplify are f(-x) 2 sign changes so this means there could be 2 or 0 negative real zeros to the polynomial.

Use Descartes’ Rule of Signs to determine how many positive and how many negative real zeros the polynomial may have. Counting multiplicities and complex (imaginary) zeros, the total number 1 starts Neg. changes Pos. of zeros will be the same as the degree of the polynomial. There is one sign change so there is one positive real zero. starts Pos. Never changes There are no negative real zeros. Descartes rule says one positive and no negative real zeros so there must be 4 complex zeros for a total of 5. We’ll learn more complex zeros in Section 4. 7.

Back to our original polynomial we want to factor: 1 We’d need to try a lot of positive or negative numbers until we found one that had 0 remainder. To help we have: The Rational Zeros Theorem What this tells us is that we can get a list of the POSSIBLE rational zeros that might work by taking factors of the constant divided by factors of the leading coefficient. Factors of the constant Factors of the leading coefficient 1, 2 1 Both positives and negatives would work for factors

1, 2 So a list of possible things to try would be any number from the top divided by any from the bottom with a + or - on it. In this case that just leaves us with 1 or 2 1 Let’s try 1 1 1 2 -3 2 -1 -1 -1 -2 2 -2 0 Since 1 is a zero, we can write the factor x - 1, and use the quotient to write the polynomial factored. YES! It is a zero since the remainder is 0 We found a positive real zero so Descartes Rule tells us there is another one

1, 2 1 1 We could try 2, the other positive possible. IMPORTANT: Just because 1 worked doesn’t mean it won’t work again since it could have a Let’s try 1 again, multiplicity. but we try it on the factored version for the remaining factor (once you have 2 1 3 -1 3 2 -2 2 0 it partly factored use that to keep going--don't start over with the original). YES! the remainder is 0 Once you can get it down to 3 numbers here, you can put the variables back in and factor or use the quadratic formula, we are done with trial and error.

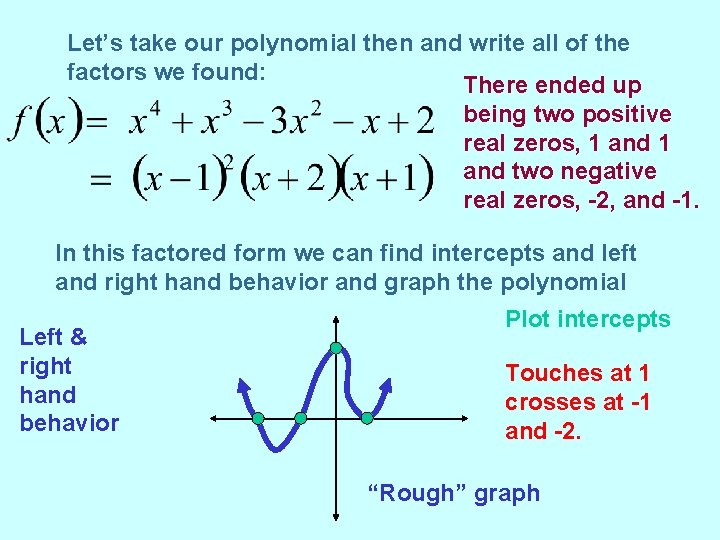
Let’s take our polynomial then and write all of the factors we found: There ended up being two positive real zeros, 1 and two negative real zeros, -2, and -1. In this factored form we can find intercepts and left and right hand behavior and graph the polynomial Left & right hand behavior Plot intercepts Touches at 1 crosses at -1 and -2. “Rough” graph

Let’s try another one from start to finish using theorems and rules to help us. Using the rational zeros 1, 3, 9 factors of constant theorem let's find factors of the constant over factors of leading 1, 2 factors of the leading coefficient to know what numbers to try. So possible rational zeros are all possible combinations of numbers on top with numbers on bottom:

starts Pos. Stays positive Let’s see if Descartes Rule helps us narrow down the choices. No sign changes in f(x) so no positive real zeros---we just ruled out half the choices to try so that helps! 1 2 3 4 starts Pos. changes Neg. changes Pos. Changes Neg. Changes Pos. 4 sign changes so 4 or 2 or 0 negative real zeros.

Let’s try -1 -1 2 2 13 -2 11 29 27 -11 -18 18 9 Let’s try -1 again -1 2 2 11 -2 9 18 -9 9 9 -9 0 Yes! We found a zero. Let’s work with reduced polynomial then. Yes! We found another one. We are done with trial and error since we can put variables back in and solve the remaining quadratic equation. So remaining zeros found by setting these factors = 0 are -3/2 and -3. Notice these were in our list of choices.

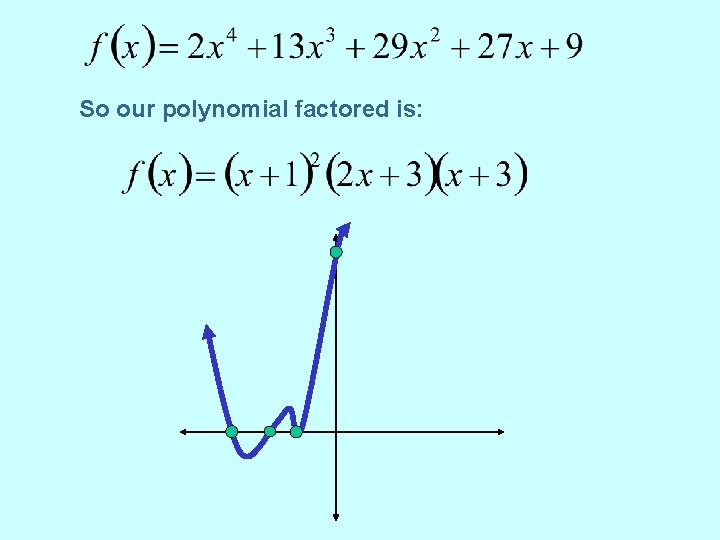
So our polynomial factored is:

Intermediate Value Theorem

Let’s solve the equation: To do that let’s consider the function If we find the zeros of the function, we would be solving the equation above since we want to know where the function = 0 By Descartes Rule: There is one sign change in f(x) so there is one positive real zero. There are 2 sign changes in f(-x) so there are 2 or 0 negative real zeros. Using the rational zeros theorem, the possible rational zeros are: 1, 5 1, 2

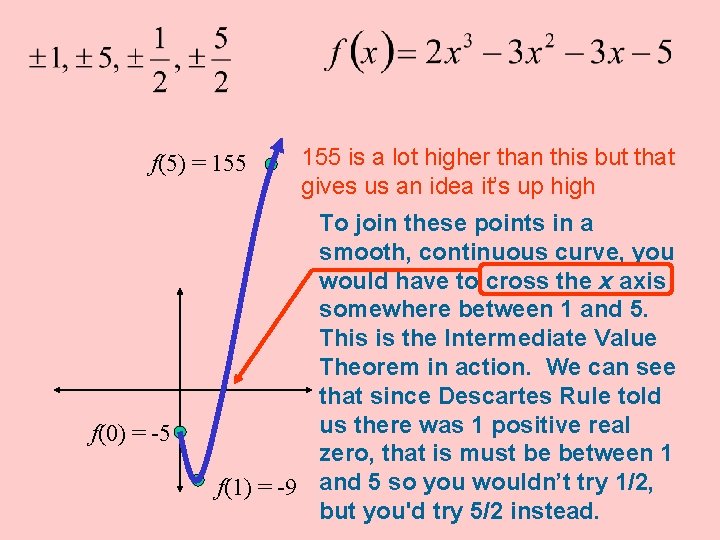
Let’s try 1 Let’s try 5 1 2 5 2 2 2 -3 -3 2 -1 -1 -4 -3 -3 10 35 7 32 -5 -4 -9 -5 160 155 1 is not a zero and f(1) = -9 5 is not a zero and f(5) = 155 On the next screen we’ll plot these points and the y intercept on the graph and think about what we can tell about this graph and its zeros.

f(5) = 155 f(0) = -5 155 is a lot higher than this but that gives us an idea it’s up high To join these points in a smooth, continuous curve, you would have to cross the x axis somewhere between 1 and 5. This is the Intermediate Value Theorem in action. We can see that since Descartes Rule told us there was 1 positive real zero, that is must be between 1 f(1) = -9 and 5 so you wouldn’t try 1/2, but you'd try 5/2 instead.

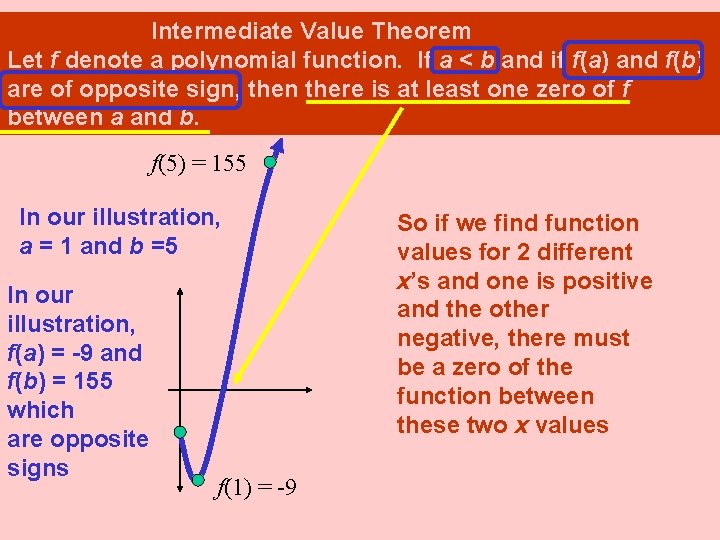
Intermediate Value Theorem Let f denote a polynomial function. If a < b and if f(a) and f(b) are of opposite sign, then there is at least one zero of f between a and b. f(5) = 155 In our illustration, a = 1 and b =5 In our illustration, f(a) = -9 and f(b) = 155 which are opposite signs f(1) = -9 So if we find function values for 2 different x’s and one is positive and the other negative, there must be a zero of the function between these two x values

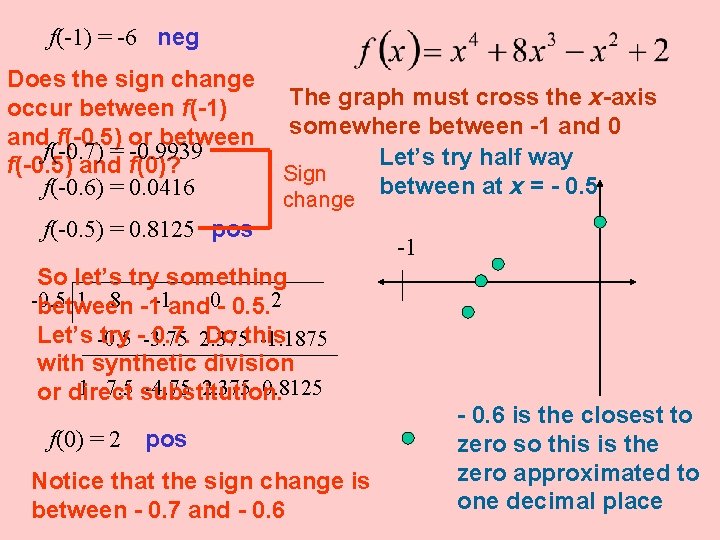
We use this theorem to approximate zeros when they are irrational numbers. The function below has a zero between -1 and 0. We’ll use the Intermediate Value Theorem to approximate the zero to one decimal place. First let’s verify that there is a zero between -1 and 0. If we find f(-1) and f(0) and they are of opposite signs, we’ll know there is a zero between them by the Intermediate Value Theorem. -1 1 8 -1 0 2 -1 -7 8 -8 1 7 -8 8 -6 So f(-1) = -6 and f(0) = 2 These are opposite signs.

f(-1) = -6 neg Does the sign change occur between f(-1) and f(-0. 5) or between f(-0. 7) = -0. 9939 f(-0. 5) and f(0)? f(-0. 6) = 0. 0416 The graph must cross the x-axis somewhere between -1 and 0 Let’s try half way Sign between at x = - 0. 5 change f(-0. 5) = 0. 8125 pos So let’s try something -0. 5 1 8 -1 -1 and 0 - 0. 5. 2 between Let’s -0. 5 try --3. 75 0. 7. 2. 375 Do this -1. 1875 with synthetic division 1 7. 5 substitution. -4. 75 2. 375 0. 8125 or direct f(0) = 2 pos Notice that the sign change is between - 0. 7 and - 0. 6 -1 - 0. 6 is the closest to zero so this is the zero approximated to one decimal place