The List ADT Definition A list is a

The List ADT Definition A list is a collection of objects, called nodes, connected in a chain by links. There may or may not be an ordering relationship between data in the nodes. Depending on this, we distinguish between ordered and unordered lists. For now, we consider only unordered lists. Operations (methods) on lists: insert. First (node) Inserts a new node at the beginning of the list delete. First (node) Deletes a node from the beginning of the list size () Returns the number of nodes in the list empty () Returns true if the list is empty search (key) Searches for a node with the specified key traverse () Processes each node on the list (for example, prints it out)

A linked list interface and the Node class public interface LList { public void insert. First (int item); public Node delete. First (); public int size(); public boolean empty (); public boolean search (int item); public void traverse (); public Node (int d, Node n) { data = d; next = n; } public void set. Data (int new. Data) { data = new. Data; } public void set. Next (Node new. Next) { next = new. Next; } } public int get. Data () { return data; } class Node { private int data; private Node next; public Node get. Next () { return next; } public Node () { this(0, null); } public Node (int d) { data = d; } public void display. Node () { System. out. print (data); } }

Implementation of an unordered linked list ADT class Link. List. ADT implements LList { private Node first; public Link. List. ADT () { first = null; } public boolean empty () { return (first == null); } public int size () { int count = 0; Node current = first; while (current != null) { count++; current = current. get. Next(); } return count; } public void insert. First (int new. Data) { Node new. First = new Node (new. Data); new. First. set. Next(first); first = new. First; } public Node delete. First () { Node temp = first; first = first. get. Next(); return temp; } public boolean search (int key) { boolean result = false; Node current = first; while (current != null) { if (current. get. Data () == key) { result = true; return result; } else current = current. get. Next(); } return result; } public void traverse () { System. out. print ("Current list: "); Node current = first; while (current != null) { current. display. Node (); System. out. print (" "); current = current. get. Next(); } System. out. println (); } }

Efficiency of linked list operations empty, insert. First and delete. First methods are O(1), while size, search and traverse methods are O(N). The size method can be rewritten in a more efficient, O(1), form, but the (linear) search and traverse methods do require a loop to process each of the nodes on the list. If we want to insert a node in a place different than the beginning of the list, we must first find that place by means of the search method, and then insert (or delete) the node. Although the actual insert / delete process involves simply an exchange of two pointers, the overall efficiency of these method will be O(N) because of the search involved. Ordered linked lists rely on an insert. N method to add the new node in the appropriate place according to the prescribed ordering relationship. Therefore, the insertion in an ordered linked list will also be O(N) operation (if linear search is used).

The Queue ADT -- a linked list implementation public interface LLQueue { public void enqueue (int item); public int dequeue(); public int size(); public boolean empty(); public int front(); } class LLQueue. ADT implements LLQueue { private int size; private Node front; private Node rear; public void enqueue (int number) { Node new. Node = new Node (); new. Node. set. Data(number); new. Node. set. Next(null); if (this. empty()) front = new. Node; else rear. set. Next(new. Node); rear = new. Node; size++; } public int dequeue () { int i; i = front. get. Data(); front = front. get. Next(); size--; if (this. empty()) rear = null; return i; } public LLQueue. ADT () { size = 0; front = null; rear = null; } public boolean empty () { return (size == 0); } public int size () { return size; } public int front () { return front. get. Data(); } }

The Stack ADT -- a linked list implementation public interface LLStack { public void push (int item); public int pop(); public int size(); public boolean empty(); public int ontop(); } public void push (int number) { Node new. Node = new Node (); new. Node. set. Data(number); new. Node. set. Next(top); top = new. Node; size++; } public int pop () { int i; i = top. get. Data(); top = top. get. Next(); size--; return i; } class LLStack. ADT implements LLStack { private Node top; private int size; public LLStack. ADT () { top = null; size = 0; } public int ontop () { int i = pop(); push(i); return i; } public boolean empty () { return (top == null); } public int size () { return size; } }

Double-ended Queues The double-ended queue (or dequeu) supports insertions and deletions at the front and at the rear of the queue. Therefore, in addition to enqueue, dequeue (which we call now insert. Last and delete. First, respectively), and first methods, we must also provide insert. First, delete. Last and last methods. The Dequeue ADT can be used for implementing both stacks and queues. Dequeue methods Stack methods Queue methods size() empty() last() first() insert. First() insert. Last() delete. First() size() empty() ontop() --push(item) pop() -- size() empty() -front() -enqueue(item) -dequeue()

An implementation of a doubly linked list Nodes in a doubly linked list have pointers to both, the next node and the previous node. For simplicity, we can add two dummy nodes to the list: the header node, which comes before the first node, and the trailer node, which comes after the last node. The doubly linked list ADT has the following interface: public interface DLList { public void insert. First (int item); public void insert. Last (int item); public DLNode delete. First (); public DLNode delete. Last (); public int size(); public int last (); public int first (); public boolean empty (); public void traverse (); }

Implementation of a doubly linked list (cont. ) class DLNode { private int data; private DLNode next, prev; public void set. Next (DLNode new. Next) { next = new. Next; } public void set. Prev (DLNode new. Prev) { prev = new. Prev; } public DLNode () { this(0, null); } public int get. Data () { return data; } public DLNode (int d) { data = d; next = null; prev = null; } public DLNode get. Next () { return next; } public DLNode (int new. Data, DLNode new. Next, DLNode new. Prev) { data = new. Data; next = new. Next; prev = new. Prev; } public void set. Data (int new. Data) { data = new. Data; } public DLNode get. Prev () { return prev; } public void display. DLNode () { System. out. print (data); } }

Implementation of a doubly linked list (cont. ) class DLList. ADT implements DLList { private DLNode header; private DLNode trailer; private int size; public DLList. ADT () { header = new DLNode(); trailer = new DLNode(); header. set. Next(trailer); header. set. Prev(null); header. set. Data(0); trailer. set. Prev(header); trailer. set. Next(null); trailer. set. Data(0); size = 0; } public boolean empty () { return (size == 0); } public int size () { return size; } public void insert. First (int new. Data) { DLNode old. First = header. get. Next(); DLNode new. First = new DLNode (new. Data, old. First, header); old. First. set. Prev(new. First); header. set. Next(new. First); size++; } public void insert. Last (int new. Data) { DLNode old. Last = trailer. get. Prev(); DLNode new. Last = new DLNode (new. Data, trailer, old. Last); old. Last. set. Next(new. Last); trailer. set. Prev(new. Last); size++; } public DLNode delete. First () { DLNode old. First = header. get. Next(); DLNode new. First = old. First. get. Next(); new. First. set. Prev(header); header. set. Next(new. First); size--; return old. First; }

Implementation of a doubly linked list (cont. ) public DLNode delete. Last () { DLNode old. Last = trailer. get. Prev(); DLNode new. Last = old. Last. get. Prev(); trailer. set. Prev(new. Last); new. Last. set. Next(trailer); size--; return old. Last; } public boolean search (int key) { boolean result = false; DLNode current = header. get. Next(); while (current != trailer) { if (current. get. Data () == key) { result = true; return result; } else current = current. get. Next(); } return result; } public int last () { return (trailer. get. Prev(). get. Data()); } public int first () { return (header. get. Next(). get. Data()); } public void traverse () { System. out. print ("Current list: "); DLNode current = header. get. Next(); while (current != trailer) { current. display. DLNode (); System. out. print (" "); current = current. get. Next(); } System. out. println (); } }

Application of stacks and queues: parsing and evaluation of arithmetic expressions Parsing of an expression is a process of checking its syntax and representing it in a form which can be uniquely interpreted. Example: Infix forms: Postfix form: Prefix form: A * B / C + D (A * B) / C + D ((A * B) / C) + D AB*C/D+ +/*ABCD Postfix and prefix forms are unique: expression can be evaluated by scanning its postfix form from left to right, or its prefix form from right to left.

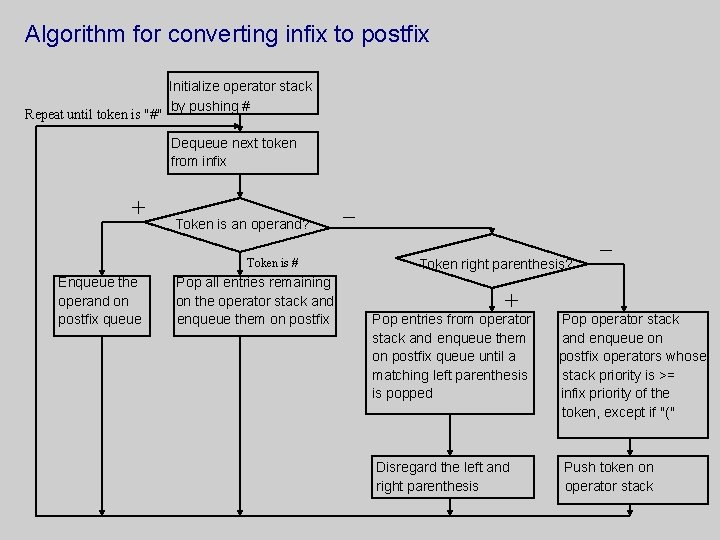
Algorithm for converting infix expressions into postfix form Data structures needed: – A queue containing the infix expression (call it infix). – A stack which may contain +, -, *, /, (, # (call it operator stack). – A queue containing the final postfix expression (call it postfix). Methods needed: – Infix. Priority, given a non-operand token, returns an integer associated with its priority according to the table below. – Stack. Priority, given a token returns integer associated with its priority according to the table below. Token * / + - ( ) # Priority Value 2 2 1 1 3 0 (undefined 0 for the stack)

Algorithm for converting infix to postfix Repeat until token is "#" Initialize operator stack by pushing # Dequeue next token from infix + Token is an operand? Token is # Enqueue the operand on postfix queue Pop all entries remaining on the operator stack and enqueue them on postfix _ _ Token right parenthesis? + Pop entries from operator stack and enqueue them on postfix queue until a matching left parenthesis is popped Disregard the left and right parenthesis Pop operator stack and enqueue on postfix operators whose stack priority is >= infix priority of the token, except if "(" Push token on operator stack

Example 1: Translate the following infix form to a postfix form: Infix queue Operator stack A # A * *# A B *# AB + +# AB* ( (+# AB* C (+# AB*C - -(+# AB*C D -(+# AB*CD / /-(+# AB*CD E /-(+# AB*CDE ) # +# A * B + (C - D / E) Postfix queue AB*CDE/-+#

The algorithm adapted for logical expressions Same data structures needed: – The infix queue. – The operator stack, which now may contain , , , (, #. – The postfix queue. Methods needed: – Infix. Priority, given a non-operand token, returns an integer associated with its priority according to the table below. – Stack. Priority, given a token returns integer associated with its priority according to the table below. Token Priority Value ( 1 2 4 3 5 6 ) # 0 (undefined 0 for the stack)

Example 2: Translate the following infix form to a postfix form: Infix queue Operator stack Postfix queue ( # P (# P Q (# PQ ( # PQ P ( # PQ P Q ( # PQ P Q ) ( ) # # # PQ P Q (P Q) ( P Q)

Evaluation of postfix expressions The idea: given the postfix expression, get a token and: 1. If the token is an operand, push its value on the (value) stack. 2. If the token is an operator, pop two values from the stack and apply that operator to them; then push the result back on the stack. Example 1: A B * C D E / - + Let A = 5, B = 3, C = 6, D = 8, E = 2. push (5) push (3) push (pop * pop) push (6) push (8) push (2) push (pop / pop) push (pop - pop) push (pop + pop) value stack 5 5 3 15 15 6 8 2 15 6 4 15 2 17

Evaluation of postfix expressions (contd. ) Example 2: P Q P Q Let P = true, Q = true value stack push (true) push (pop pop) push (pop pop) true true true false true To determine if the expression is a tautology, it must evaluate to true for all combinations of truth values of its components, i. e for P = false and Q = true; P = true and Q = false; P = false and Q= false.