TESTOVANIE TATISTICKCH HYPOTZ 1 PREDNKA 5 p testovanie

TESTOVANIE ŠTATISTICKÝCH HYPOTÉZ 1

PREDNÁŠKA 5 p testovanie štatistických hypotéz: p p p základná terminológia chyba I. a II. druhu všeobecný postup testovania p testy hypotéz o strednej hodnote n n n p test zhody strednej hodnoty so známou konštantou test zhody dvoch stredných hodnôt – nezávislé výbery test zhody dvoch stredných hodnôt – závislé výbery testy hypotéz o rozptyle n n test zhody rozptylu so známou konštantou test zhody dvoch rozptylov 2

Testovanie štatistických hypotéz n n vychádzame z toho, že parametre ZS nie sú známe môžeme však o nich vysloviť určité predpoklady overujeme štatistickými metódami, ktoré nazývame štatistické hypotézy postup = testovanie štatistických hypotéz 3

Testovanie štatistických hypotéz n n vychádzame zo základnej hypotézy = H 0 hypotéza oproti nej je postavená alternatívna hypotéza H 1 cieľom testovanie hypotéz je rozhodnutie o prijatí alebo zamietnutí základnej hypotézy ak zamietame základnú hypotézu, potom prijímame alternatívnu hypotézu 4

Testovanie štatistických hypotéz štatistická hypotéza môže vyjadrovať predpoklad o rovnosti parametra ZS s ľubovoľnou známou konštantou alebo parametrom iného základného súboru n v tomto prípade hovoríme o H 0 hypotéze H 0: Q=Q 0 H 0: Q-Q 0=0 n také hypotézy, pri ktorých sa predpokladá nerovnosť parametra ZS, sa nazývajú H 1 hypotézy n 5

Testovanie štatistických hypotéz n H 1 hypotézy môžu byť v rôznych tvaroch: H 1: Q Q 0 ¨ jednostranné: ¨ obojstranná n n pravostranná H 1: Q Q 0 ľavostranná H 1: Q<Q 0 6

Testovanie štatistických hypotéz parameter Q, o ktorom máme určitú hypotézu, nepoznáme n odhadujeme ho pomocou výberovej charakteristiky un n un je náhodná premenná, pričom predpokladáme, že poznáme jej rozdelenie n 7

Testovanie štatistických hypotéz n n n rozhodnutie o zamietnutí, resp. nezamietnutí H 0 uskutočňujeme na základe náhodného výberu nemôžeme ho urobiť s absolútnou presnosťou existuje určité riziko odhadu za predpokladu, že platí H 0, rovná sa parameter Q predpokladanej veličine Q 0 keďže est Q=un, potom rozdiel =un-Q 0 je len náhodnou chybou spôsobenou náhodným výberom 8

Testovanie štatistických hypotéz n ak však H 0 neplatí, t. j. Q Q 0, potom sa rozdiel môže skladať z náhodnej chyby a systematickej chyby, chyby ktorá odráža skutočný rozdiel medzi parametrom ZS Q a jeho predpokladanou veľkosťou Q 0 = un-Q 0=(un-Q)+(Q-Q 0) náhodná chyba systematická chyba - rozdiel 9

Testovanie štatistických hypotéz v praxi nemožno zistiť, či rozdiel obsahuje iba náhodnú chybu alebo aj systematickú n ak je však malé, pripisujeme ho iba náhodnosti výberu n ak prekročí určitú veľkosť, predpokladáme, že zahrňuje aj systematickú chybu - rozdiel n 10

Testovanie štatistických hypotéz n rozhodnutie o zamietnutí, resp. nezamietnutí H 0 predpokladá znalosť kritickej hodnoty, hodnoty ktorá rozdiel rozdelí na dve časti : ¨ ¨ n pri rozdieloch < ako kritická hodnota, H 0 nezamietame pri rozdieloch ako kritická hodnota, H 0 zamietame veľkosť v konkrétnych prípadoch kolíše, je náhodnou veličinou, preto sa snažíme transformovať na veličinu G, ktorá má známe teoretické rozdelenie (napr. normované normálne, resp. Studentovo či iné rozdelenie) 11

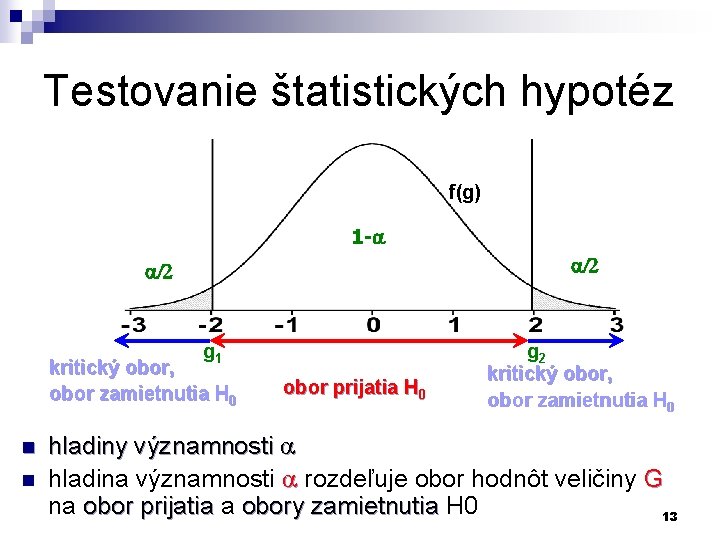
Testovanie štatistických hypotéz n n n G = f(un, Q) G = f( ) pričom funkcia hustoty náhodnej premennej G je f(g) vychádzame z platnosti H 0: Q = Q 0 a vypočítame testovaciu charakteristiku g =f(un, Q 0) rozhodnutie o výsledku testu: ¨ môžeme potom nájsť také kritické hodnoty g 1 a g 2 náhodnej veličiny G, pre ktoré platí: P(g 1 G g 2) =1 - alebo P(g 1 G g 2) = 12

Testovanie štatistických hypotéz f(g) 1 - /2 g 1 kritický obor, obor zamietnutia H 0 n n obor prijatia H 0 g 2 kritický obor, obor zamietnutia H 0 hladiny významnosti hladina významnosti rozdeľuje obor hodnôt veličiny G na obor prijatia a obory zamietnutia H 0 13

Testovanie štatistických hypotéz n Závery testov je možné robiť dvomi spôsobmi: a) b) klasický (na základe kritickej hodnoty) moderný prostredníctvom p hodnoty (p value) P hodnota predstavuje pravdepodobnosť, že výberová charakteristika nadobudne aspoň takú hodnotu ako je skutočne zistená hodnota (hodnota testovacej charakteristiky) p hodnota = P(U>u) p hodnota = vypočítaná hladina významnosti prakticky: ak p hodnota < hladina významnosti ( ), tak H 0 zamietame ak p hodnota < 0, 05 rozdiel je preukazný ak p hodnota < 0, 01 rozdiel je vysokopreukazný 14

Testovanie štatistických hypotéz n n CHYBY PRI TESTOVANÍ: popri správnom rozhodnutí o výsledku testu: ¨ prijatí správnej hypotézy ¨ zamietnutí nesprávnej hypotézy n môže dôjsť k nesprávnemu rozhodnutiu: ¨ zamietnutí správnej hypotézy – chyby I. druhu ¨ prijatí nesprávnej hypotézy – chyby II. druhu 15

Testovanie štatistických hypotéz n n n 1 - – pravdepodobnosť prijatia správnej hypotézy – riziko zamietnutia správnej hypotézy ak sa znižuje , znižuje sa vznik chyby I. druhu = rozšíri sa obor prijatia H 0 znižovaním však rastie riziko vzniku chyby II. druhu – označuje sa ako b potom 1 -b udáva silu testu = pravdepodobnosť zamietnutia H 0 v prípade, ak je skutočne nesprávna v praxi: =0, 05, =0, 05 resp. =0, 01 16

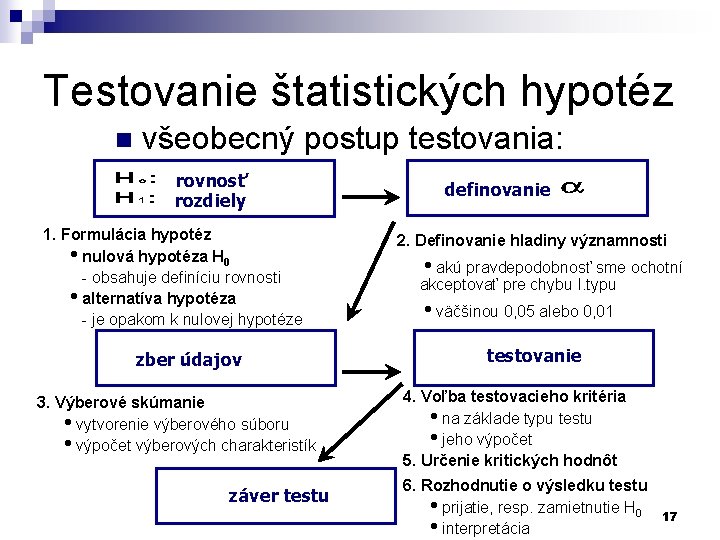
Testovanie štatistických hypotéz n všeobecný postup testovania: rovnosť rozdiely 1. Formulácia hypotéz hnulová hypotéza H 0 - obsahuje definíciu rovnosti halternatíva hypotéza - je opakom k nulovej hypotéze zber údajov 3. Výberové skúmanie hvytvorenie výberového súboru hvýpočet výberových charakteristík záver testu definovanie 2. Definovanie hladiny významnosti hakú pravdepodobnosť sme ochotní akceptovať pre chybu I. typu hväčšinou 0, 05 alebo 0, 01 testovanie 4. Voľba testovacieho kritéria hna základe typu testu hjeho výpočet 5. Určenie kritických hodnôt 6. Rozhodnutie o výsledku testu hprijatie, resp. zamietnutie H 0 hinterpretácia 17

Testy hypotéz o strednej hodnote n test zhody strednej hodnoty so známou konštantou Ø Ø Ø n poznáme 2 nepoznáme 2 a n>30 nepoznáme 2 a n 30 test zhody dvoch stredných hodnôt Ø nezávislé súbory: n n n Ø poznáme 21, 22 nepoznáme 21, 22 a n 1, n 2>30 nepoznáme 21, 22 a n 1, resp. n 2 30 závislé súbory 18

Test zhody strednej hodnoty so známou konštantou A. Test zhody strednej hodnoty so známou konštantou ¨ ¨ ¨ nech štatistický znak X má v ZS približne normálne rozdelenie X. . N ( , 2) predpokladajme, že stredná hodnota sa rovná známej konštante 0 formulácia hypotéz: H 0 : m = m 0 H 1 : m ¹ m 0 ¨ odhadujeme, že est = 19

Test zhody strednej hodnoty so známou konštantou a) predpokladáme, že poznáme 2 ZS (teoretický predpoklad) ¨ testovacia charakteristika ¨ u má N(0, 1) 20

Test zhody strednej hodnoty so známou konštantou b) nepoznáme 2 ZS a rozsah VS >30 est 2 = s 12 ¨ testovacia charakteristika ¨ ¨ u má N(0, 1) 21

Test zhody strednej hodnoty so známou konštantou c) nepoznáme 2 ZS a rozsah VS 30 est 2 = s 12 ¨ testovacia charakteristika ¨ ¨ t má t (n-1) rozdelenie (Studentove r. ) 22

Test zhody strednej hodnoty so známou konštantou n rozhodnutie o výsledku testu: f(u) 1 - /2 -u 1 - /2 kritický obor, obor zamietnutia H 0 vak u 1 - /2 obor prijatia H 0 kritický obor, obor zamietnutia H 0 |uvyp, tvyp| < u 1 - /2, t , (n-1) H 0 nezamietame | uvyp, tvyp| u 1 - /2, t , (n-1) H 0 zamietame 23

Test zhody dvoch stredných hodnôt B. Test zhody dvoch stredných hodnôt – nezávislé výbery predpokladáme, že výberové súbory sú nezávislé: ¨ n n ¨ ¨ prvky jedného súboru nemôžu byť zároveň prvkami druhého súboru prvky sa v danom súbore neopakujú nech štatistický znak X 1 v prvom ZS má normálne rozdelenie N ( 1 , 1 2 ) nech štatistický znak X 2 v druhom ZS má normálne rozdelenie N ( 2 , 2 2 ) 24

Test zhody dvoch stredných hodnôt predpokladajme, že odhadované stredné hodnoty 1 a 2 sú zhodné ¨ formulácia hypotéz: ¨ H 0: m 1 = m 2 H 1: m 1 ¹ m 2 ¨ H 0: m 1 - m 2 = 0 , resp. H 1: m 1 - m 2 ¹ 0 , resp. odhadujeme, že: n n est 1 = est 2 = 25

Test zhody dvoch stredných hodnôt a) predpokladáme, že poznáme rozptyly ZS 1 a ZS 2 (teoretický predpoklad) potom aj ¨ testovacia charakteristika ¨ u má N(0, 1) 26

Test zhody dvoch stredných hodnôt b) nepoznáme rozptyly ZS 1 a ZS 2 a rozsahy VS 1 a VS 2 >30 ¨ ¨ est 12 = s 112, est 22 = s 122 testovacia charakteristika (po úprave), inak rovnaká ako v prípade a) ¨ u má N(0, 1) 27

Test zhody dvoch stredných hodnôt c) nepoznáme rozptyly ZS a rozsah 1 2 VS 1 30 alebo rozsah VS 2 30 est 12 = s 112, est 22 = s 122 podmienka: rozptyly porovnávaných základných súborov sa rovnajú testovacia charakteristika: t má t (s. v. ) rozdelenie (Studentove r. ) stupne voľnosti = n 1+n 2 -2 28

Test zhody dvoch stredných hodnôt d) predpokladajme, že rozptyly základných súborov 12 , 22 nepoznáme, pričom aspoň jeden z výberových súborov má malý rozsah n 1 30, alebo n 2 30. Nemôžeme však predpokladať zhodu rozptylov( 12 22 ) (Overuje sa F-testom). Môžeme použiť približný Behrens-Fischerov test zhody stredných hodnôt pri nehomogénnej variancii. 29

Test zhody dvoch stredných hodnôt C. Test zhody dvoch stredných hodnôt – závislé výbery = párový t-test predpokladáme, že výberové súbory sú závislé: ¨ n n n skúmanie na tej istej štatistickej jednotke dva krát prvky sa v daných súboroch opakujú rozsahy výberových súborov sa musia rovnať 30

Test zhody dvoch stredných hodnôt n n test je založený na diferencii di=xi 1 -xi 2 formulácia hypotéz: H 0: m 1 = m 2 , resp. H 0: md = 0 H 1: m 1 ¹ m 2 , resp. H 1: md ¹ 0 n testovacia charakteristika n t má t (n-1) rozdelenie (Studentove r. ) 31

Testy hypotéz o rozptyle test zhody rozptylu so známou konštantou n test zhody dvoch rozptylov n 32

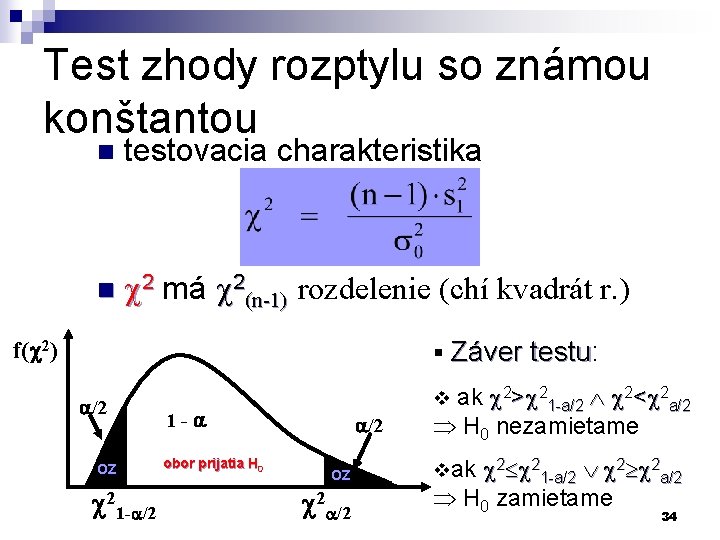
Test zhody rozptylu so známou konštantou A. Test zhody rozptylu so známou konštantou ¨ ¨ ¨ nech štatistický znak X má v ZS približne normálne rozdelenie X. . N ( , 2) predpokladajme, že rozptyl 2 sa rovná známej konštante 0 2 formulácia hypotéz: H 0 : s 2 = s 0 2 H 1 : s 2 ¹ s 0 2 ¨ odhadujeme, že est 2 = s 12 33

Test zhody rozptylu so známou konštantou n testovacia charakteristika n c 2 má c 2(n-1) rozdelenie (chí kvadrát r. ) § Záver testu: testu f( 2) /2 OZ 21 - /2 1 - obor prijatia H 0 ak c 2>c 21 -a/2 Ù c 2<c 2 a/2 H 0 nezamietame v /2 OZ 2 /2 c 21 -a/2 Ú c 2 a/2 H 0 zamietame vak 34

Test zhody dvoch rozptylov B. ¨ ¨ - nech štatistický znak X 1 v prvom ZS má normálne rozdelenie N ( 1 , 1 2 ) nech štatistický znak X 2 v druhom ZS má normálne rozdelenie N ( 2 , 2 2 ) predpokladajme, že odhadované rozptyly 12 a 22 sú zhodné formulácia hypotéz: H 0 : s 1 2 = s 1 2 H 1: s 12 > s 12 (jednostranný test) odhadujeme, že: est 12 = s 112 a est 22 = s 122 35

Test zhody dvoch rozptylov n n f(F) testovacia charakteristika F má F , (n 1 -1), (n 2 -1) rozdelenie (Fischerove r. ) § Záver testu: 1 - obor prijatia H 0 OZ F , (n 1 -1), (n 2 -1) ak F< F , (n 1 -1), (n 2 -1) H 0 nezamietame v ak F F , (n 1 -1), (n 2 -1) H 0 zamietame 36 v

ĎAKUJEM ZA POZORNOSŤ 37