TESTOVANIE TATISTICKCH HYPOTZ 1 neparametrick testy 2 neparametrick

TESTOVANIE ŠTATISTICKÝCH HYPOTÉZ 1 – neparametrické testy

2 neparametrické testy je skupina testov, ktoré nevyžadujú splnenie predpokladu o charaktere rozdelenia náhodných veličín obvykle sa požaduje len to, aby rozdelenie bolo spojitého typu názov je odvodený od toho, že sa netýkajú parametrov rozdelení náhodných veličín (stredná hodnota, rozptyl), ale poradia – z toho aj názov poradové testy

3 Poradové testy – pracujeme nie s konkrétnymi hodnotami, ale s ich poradím (zoradené podľa veľkosti a očíslované) Sú vhodné v prípade: - - keď nepoznáme typ rozdelenia NV a nemôžeme použiť parametrický test, sledovaná veličina nie je číselná, ale jej úrovne vieme zoradiť podľa veľkosti a pridať im poradové čísla (tvrdosť, farba, hustota, chuť, estetická vlastnosť), hodnoty veličiny sú subjektívne (nespoľahlivé), ale ich poradie je objektívne a správne (hodnotenie počtu bodov chovateľských súťaží, školská klasifikácia, degustačná súťaž)

4 Prednosti neparametrických testov: - nezávislosť na tvare rozdelenia - použiteľné pre kvalitatívne aj kvantitatívne znaky - po výpočtovej stránke sú jednoduchšie a rýchlejšie ako parametrické testy - majú všeobecnejšie použitie

5 Nevýhody neparametrických testov: - menšia sila, menšia schopnosť zamietnuť nesprávnu nulovú hypotézu v porovnaní s parametrickými testami - ak sú splnené predpoklady použitia parametrických testov a chceme použiť obdobu neparametrického testu, potrebujeme väčší rozsah náhodného výberu (aby sme dosiahli rovnakú silu testu)

6

7

8 Príklad Predpokladajme, že máme k dispozícii namerané hodnoty usporiadané podľa veľkosti: 3, 15 3, 20 3, 25 3, 30 4, 00. Overte, či extrémnu hodnotu 4, 00, ktorá sa na prvý pohľad javí výrazne odlišná od ostatných hodnôt, je nutné zo súboru vylúčiť (či je extrémna) Kritická hodnota Dixonovho testu pre alfa = 0, 05, a n=5 je Vypočítaná hodnota testovacieho kritéria je väčšia ako kritická 0, 8235 > 0, 642, to znamená že hodnotu 4, 00 zo súboru vylúčime ako extrémnu. Poznámka: nulová hypotéza predpokladala, že hodnota nie je extrémna Dixonov test (Q test) používame pri testovaní súboru s neznámym rozdelením (prípadne súboru s malým počtom meraní)

9 Test dobrej zhody testy hypotéz – zhody rozdelení (= testy dobrej zhody / fit testy / Goodness of Fit Tests) Okrem parametrov je možné testovať aj zhodu rozdelení Overujeme, či empirické rozdelenie je štatisticky zhodné s niektorým z teoretických rozdelení pravdepodobnosti, prípadne s iným empirickým rozdelením. χ2 test dobrej zhody – overujeme predpoklad o zhode rozdelenia test dobrej zhody náhodnej veličiny so známym teoretickým rozdelením (napr. Normálnym rozdelením, . . . )

10 Test dobrej zhody Možno nimi riešiť napr. nasledovné úlohy: či empirický súbor pochádza zo ZS s určitými charakteristikami, či určité teoretické rozdelenie pravdepodobností možno použiť ako model pre sledovaný výberový súbor, či dva náhodné výbery pochádzajú z jedného súboru, a pod.

11 Test zhody rozdelenia Označenie: G(x) empirické rozdelenie H(x) teoretické rozdelenie Formulácia hypotéz: H 0: G(x) = H(x) H 1: G(x) ≠ H(x)

12 Všeobecný postup 1. Navrhnúť predpokladaný typ rozdelenia pravdepodobnosti, napr. na základe grafického zobrazenia rozdelenia početností empirických údajov 2. Odhadnúť parametre vybraného rozdelenia (intervaly spoľahlivosti) 3. Overiť zhodu rozdelenia výberových údajov s vybraným rozdelením s odhadnutými parametrami pomocou testov dobrej zhody

13 Testy dobrej zhody Hodnoty skúmanej vybranej premennej - náhodne vybranej vzorky rozsahu n, sú rozdelené do k tried (variačné triedenie) Porovnáva sa miera zhody pozorovaných –empirických početností ni týchto tried s teoretickými početnosťami npi zodpovedajúcimi týmto triedam (pi – teoretická pravdepodobnosť výskytu hodnôt z i-tej triedy podľa skúmaného zákona rozdelenia pravdepodobnosti (normálne, Poissonove, binomické rozdelenie a iné)

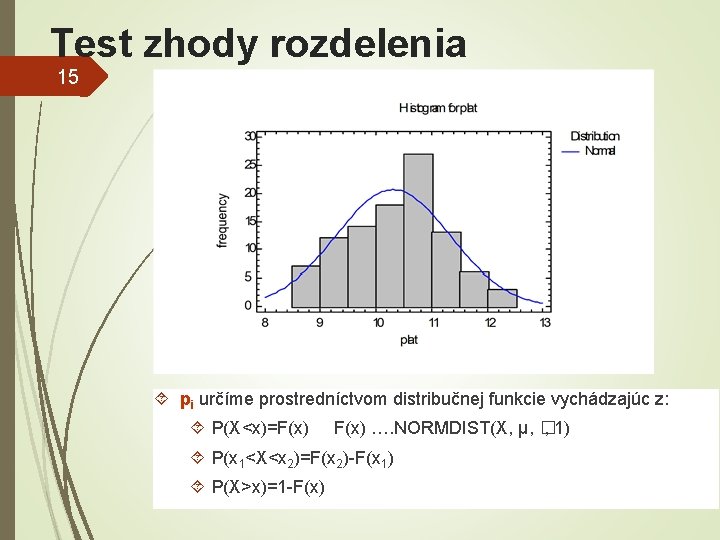
Test zhody rozdelenia 14 Testovacie kritérium: ni empirické absolútne početnosti pi – pravdepodobnosť výskytu i-tého intervalu (spojité rozdelenie) npi teoretické absolútne početnosti, ktoré vypočítame ako súčin rozsahu výberového súboru (n) a pravdepodobnosti výskytu (pi) Podmienka testu - Cochranovo pravidlo v každej triede npi > 5 (pri nesplnení zlučujeme triedy) Platí: Testovacie kritérium má χ2 rozdelenie s m-p-s-1 stupňami voľnosti, (mpočet intervalov, p-počet parametrov teoretického rozdelenie, s-počet p zlučovaných tried).

Test zhody rozdelenia 15 pi určíme prostredníctvom distribučnej funkcie vychádzajúc z: P(X<x)=F(x) …. NORMDIST(X, µ, � , 1) P(x 1<X<x 2)=F(x 2)-F(x 1) P(X>x)=1 -F(x)

16 Test zhody rozdelenia Záver: χ2 χ2(� , ν) → H 0 zamietame Rozdelenie súboru sa neriadi normálnym rozdelením χ2< χ2(� , ν) → H 0 nezamietame Rozdelenie súboru sa riadi normálnym rozdelením