Teach GCSE Maths Alternate Segment Theorem Teach GCSE

  • Slides: 17
Download presentation
Teach GCSE Maths Alternate Segment Theorem

Teach GCSE Maths Alternate Segment Theorem

Teach GCSE Maths Alternate Segment Theorem "Certain images and/or photos on this presentation are

Teach GCSE Maths Alternate Segment Theorem "Certain images and/or photos on this presentation are the copyrighted property of Jupiter. Images and are being used with permission under license. These images and/or photos may not be copied or downloaded without permission from Jupiter. Images" © Christine Crisp

When we draw a chord joining 2 points on the circumference of a circle,

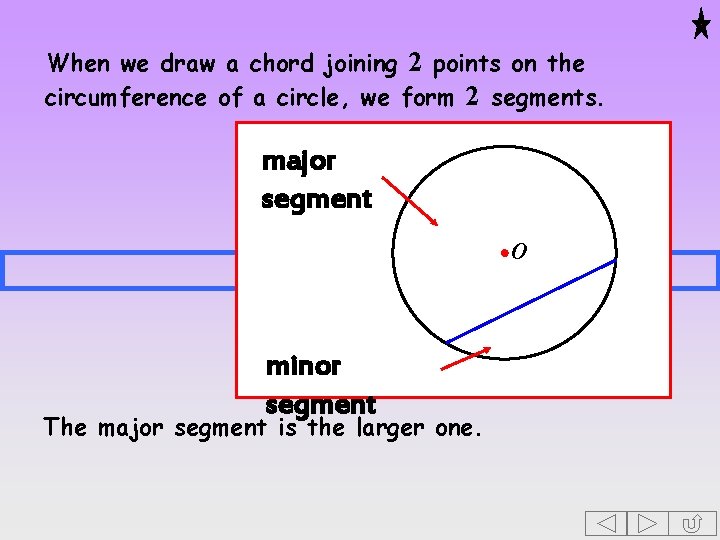
When we draw a chord joining 2 points on the circumference of a circle, we form 2 segments. major segment O minor segment The major segment is the larger one.

If we now draw a tangent at one end of the chord. . .

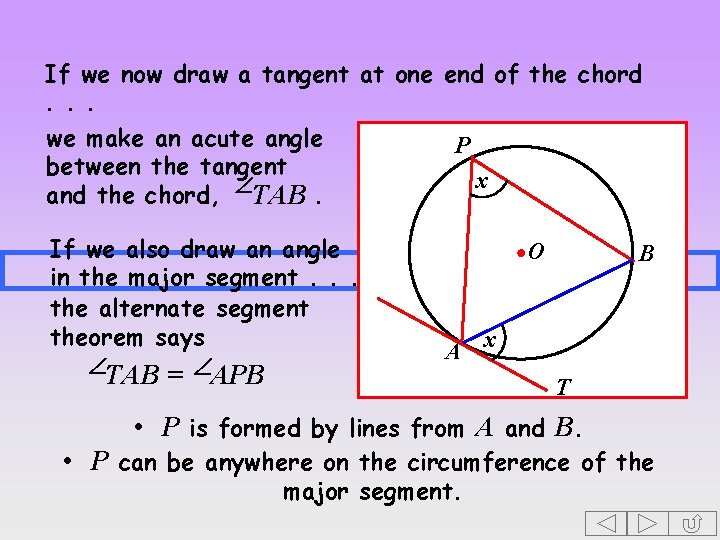
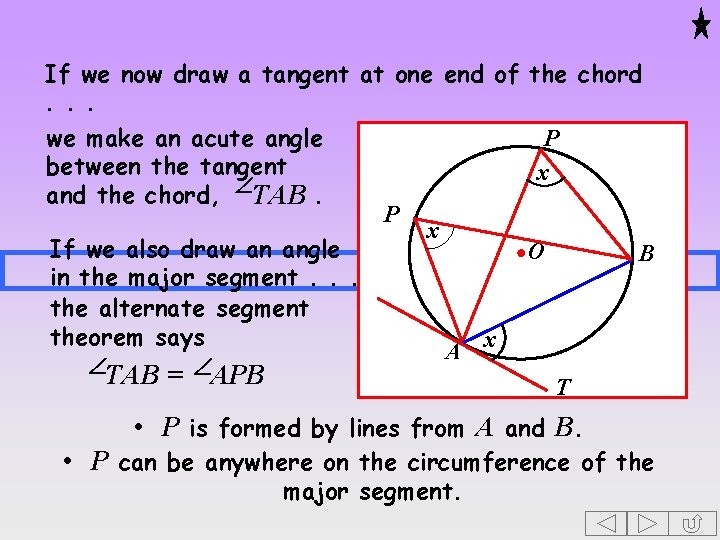
If we now draw a tangent at one end of the chord. . . we make an acute angle P between the tangent x and the chord, TAB. If we also draw an angle in the major segment. . . the alternate segment theorem says TAB = APB O A B x T • P is formed by lines from A and B. • P can be anywhere on the circumference of the major segment.

If we now draw a tangent at one end of the chord. . .

If we now draw a tangent at one end of the chord. . . we make an acute angle P between the tangent x and the chord, TAB. P x If we also draw an angle O B in the major segment. . . the alternate segment theorem says x A TAB = APB T • P is formed by lines from A and B. • P can be anywhere on the circumference of the major segment.

The same is true for the obtuse angle but it is equal to the

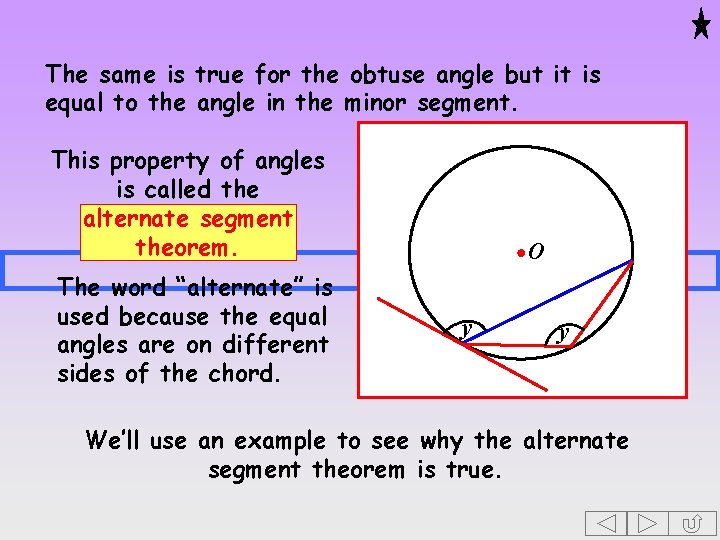
The same is true for the obtuse angle but it is equal to the angle in the minor segment. This property of angles is called the alternate segment theorem. The word “alternate” is used because the equal angles are on different sides of the chord. O y y We’ll use an example to see why the alternate segment theorem is true.

Each time the animation pauses, decide with your We want to the showreason that

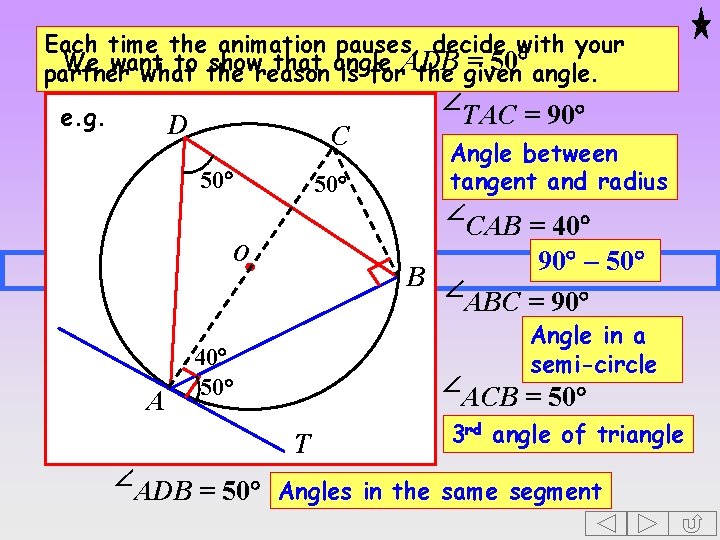
Each time the animation pauses, decide with your We want to the showreason that angle = 50 angle. partner what is for. ADB the given TAC = 90 e. g. D C Angle between 50 tangent and radius 50 CAB = 40 90 - 50 B ABC = 90 O A 40 50 T Angle in a semi-circle ACB = 50 3 rd angle of triangle ADB = 50 Angles in the same segment

To prove the alternate segment theorem we use the same steps as in the

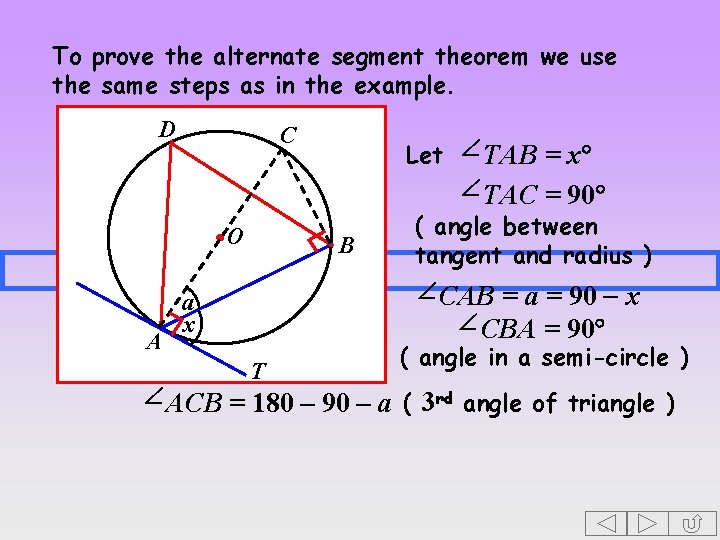
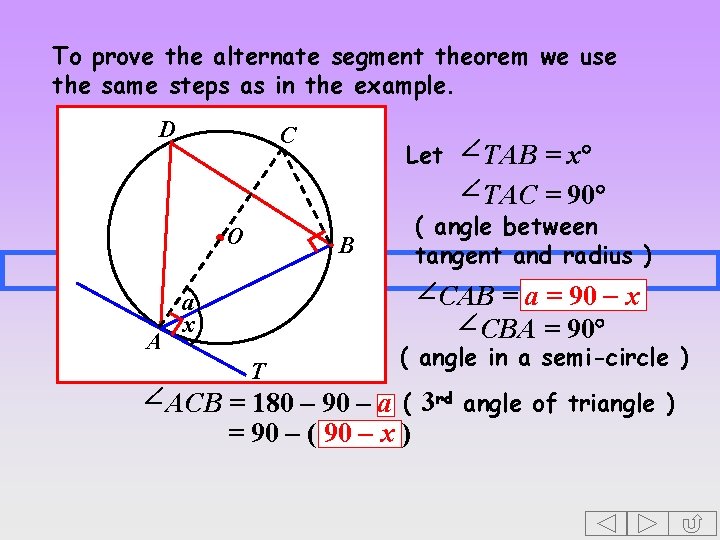
To prove the alternate segment theorem we use the same steps as in the example. D C O A Let TAB = x TAC = 90 B a x T ( angle between tangent and radius ) CAB = a = 90 - x CBA = 90 ( angle in a semi-circle ) ACB = 180 – 90 – a ( 3 rd angle of triangle )

To prove the alternate segment theorem we use the same steps as in the

To prove the alternate segment theorem we use the same steps as in the example. D C O A Let TAB = x TAC = 90 B a x T ( angle between tangent and radius ) CAB = a = 90 - x CBA = 90 ( angle in a semi-circle ) ACB = 180 – 90 – a ( 3 rd angle of triangle ) = 90 – ( 90 - x )

To prove the alternate segment theorem we use the same steps as in the

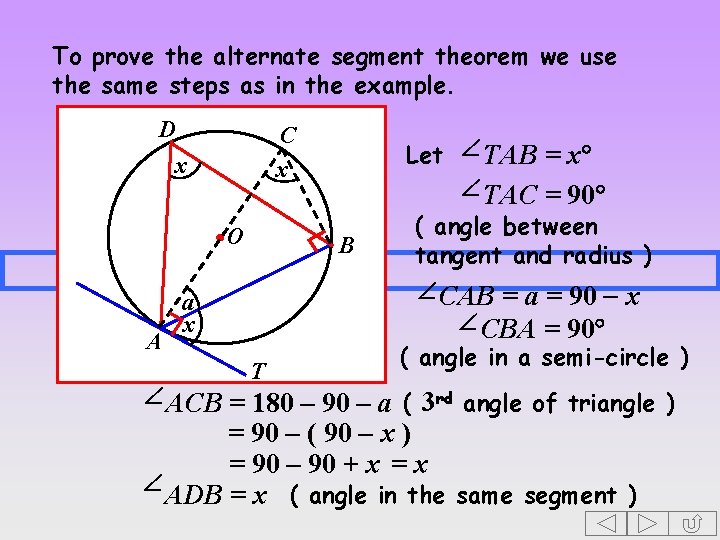
To prove the alternate segment theorem we use the same steps as in the example. D C x x O A Let TAB = x TAC = 90 B a x T ( angle between tangent and radius ) CAB = a = 90 - x CBA = 90 ( angle in a semi-circle ) ACB = 180 – 90 – a ( 3 rd angle of triangle ) = 90 – ( 90 - x ) = 90 – 90 + x = x ADB = x ( angle in the same segment )

To prove the alternate segment theorem we use the same steps as in the

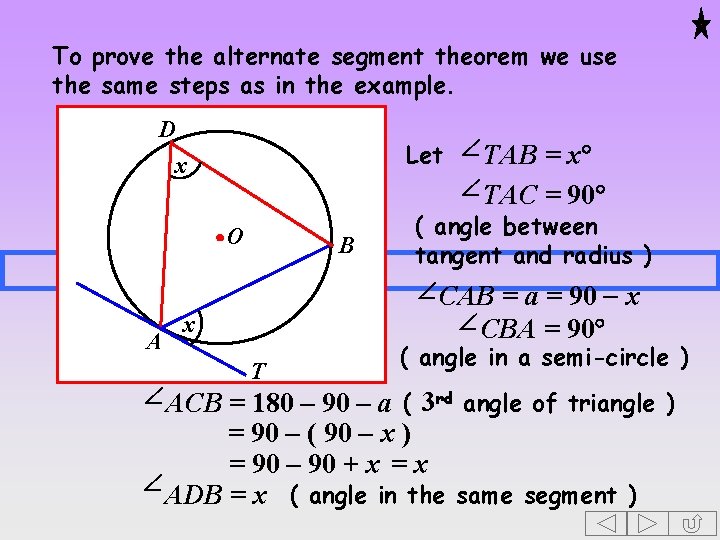
To prove the alternate segment theorem we use the same steps as in the example. D Let TAB = x TAC = 90 x O A B x T ( angle between tangent and radius ) CAB = a = 90 - x CBA = 90 ( angle in a semi-circle ) ACB = 180 – 90 – a ( 3 rd angle of triangle ) = 90 – ( 90 - x ) = 90 – 90 + x = x ADB = x ( angle in the same segment )

SUMMARY The theorems involving tangents are: • The angle between a tangent and the

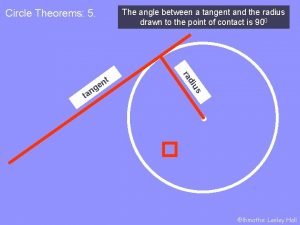
SUMMARY The theorems involving tangents are: • The angle between a tangent and the radius at the point of contact is always 90. • The tangents from an external point are equal in length. • The angle between a tangent and chord equals the angle in the alternate segment.

SUMMARY When solving problems we might also use the following: • The perpendicular from

SUMMARY When solving problems we might also use the following: • The perpendicular from the centre to a chord bisects the chord. • The angle at the centre is twice the angle at the circumference. • Angles in the same segment are equal. • The angle in a semi-circle is always 90. • The sum of the opposite angles of any cyclic quadrilateral is 180.

e. g. In the following, the red line is a tangent. Find a and

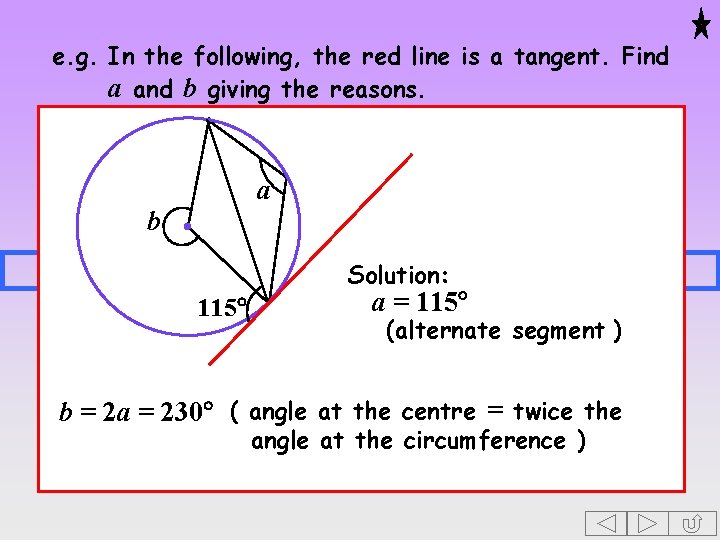
e. g. In the following, the red line is a tangent. Find a and b giving the reasons. a b Solution: 115 a = 115 (alternate segment ) b = 2 a = 230 ( angle at the centre = twice the angle at the circumference )

EXERCISE 1. In the following, O is the centre of the circle and TB

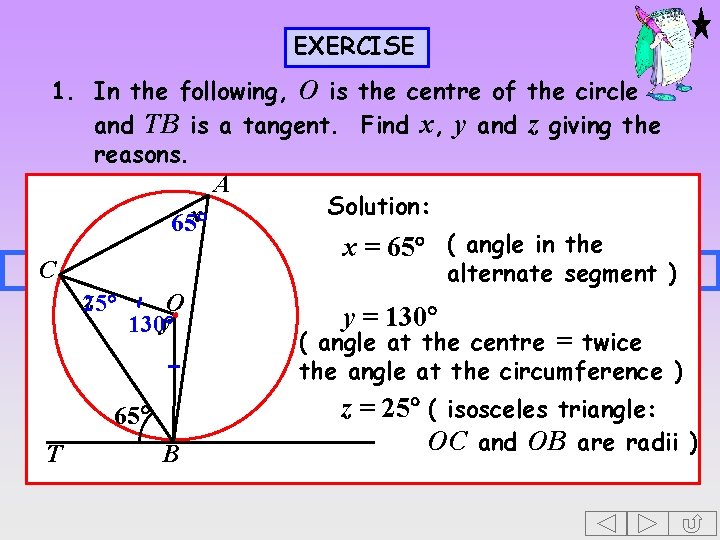
EXERCISE 1. In the following, O is the centre of the circle and TB is a tangent. Find x, y and z giving the reasons. A x 65 C z 25 O y 130 65 T B Solution: x = 65 ( angle in the alternate segment ) y = 130 ( angle at the centre = twice the angle at the circumference ) z = 25 ( isosceles triangle: OC and OB are radii )

EXERCISE 2. In the following, find angles TBA, BCA and ADB giving the reasons.

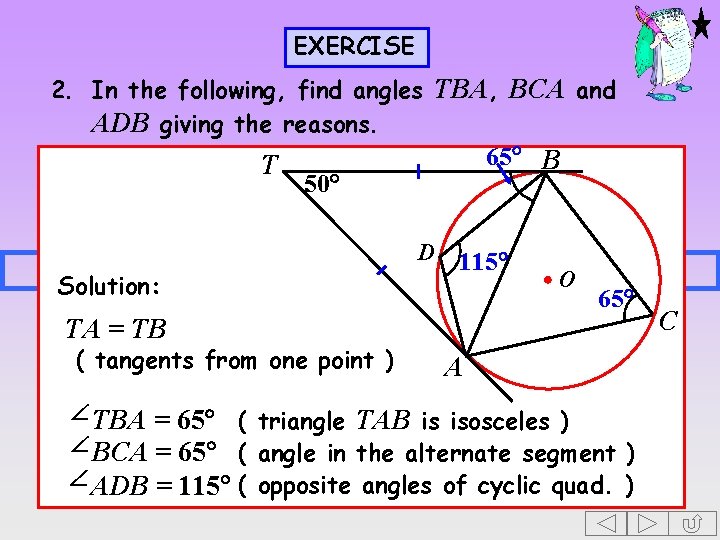
EXERCISE 2. In the following, find angles TBA, BCA and ADB giving the reasons. T 65 B 50 Solution: D 115 O 65 TA = TB ( tangents from one point ) A TBA = 65 ( triangle TAB is isosceles ) BCA = 65 ( angle in the alternate segment ) ADB = 115 ( opposite angles of cyclic quad. ) C

Teach GCSE Maths Speed Teach GCSE Maths SpeedTeach GCSE Maths Speed Teach GCSE Maths Speed
Alternate Standards Alternate Assessment Alternate Diploma AAAAAS LearningAlternate Standards Alternate Assessment Alternate Diploma AAAAAS Learning
Kohonen Network Population Segment 2 Segment 1 SegmentKohonen Network Population Segment 2 Segment 1 Segment
7 segment Display Arrangment of segment 7 segment7 segment Display Arrangment of segment 7 segment
Circle Theorems Alternate Segment Theorem Demonstration This resourceCircle Theorems Alternate Segment Theorem Demonstration This resource
GCSE Combined Science GCSE Biology GCSE Chemistry GCSEGCSE Combined Science GCSE Biology GCSE Chemistry GCSE
SHAPE SPACE Pythagorean Theorem Pythagorean Theorem Pythagorean TheoremSHAPE SPACE Pythagorean Theorem Pythagorean Theorem Pythagorean Theorem
LEMIs Theorem Lamis Theorem Statement Lamis theorem isLEMIs Theorem Lamis Theorem Statement Lamis theorem is
VARIGNONS THEOREM What is Varigons Theorem The theoremVARIGNONS THEOREM What is Varigons Theorem The theorem
Thvenins Theorem Thevenins Theorem Thevenins theorem simplifies theThvenins Theorem Thevenins Theorem Thevenins theorem simplifies the
LEMIs Theorem Lamis Theorem Statement Lamis theorem isLEMIs Theorem Lamis Theorem Statement Lamis theorem is
Bayes Theorem Basics Total probability Theorem Bayes TheoremBayes Theorem Basics Total probability Theorem Bayes Theorem
BINOMIAL THEOREM BINOMIAL THEOREM INTRODUCTION BINOMIAL THEOREM BINOMIALBINOMIAL THEOREM BINOMIAL THEOREM INTRODUCTION BINOMIAL THEOREM BINOMIAL
Teach A Level Maths Yr 1AS Pure MathsTeach A Level Maths Yr 1AS Pure Maths
Alternate Accountability Understanding the Alternate Accountability Process inAlternate Accountability Understanding the Alternate Accountability Process in
Alternate Accountability Understanding the Alternate Accountability Process inAlternate Accountability Understanding the Alternate Accountability Process in