Teach GCSE Maths Speed Teach GCSE Maths Speed

Teach GCSE Maths Speed

Teach GCSE Maths Speed "Certain images and/or photos on this presentation are the copyrighted property of Jupiter. Images and are being used with permission under license. These images and/or photos may not be copied or downloaded without permission from Jupiter. Images" © Christine Crisp

Suppose we travel 80 km in 1 hour. At times we could be travelling very fast and at others we might have stopped at traffic lights. Sometimes we will be accelerating and sometimes slowing down. However, from the information that we travelled 80 km in 1 hour, we can find the average speed. The average speed is 80 km per hour. If I travel the next 40 km in 1 hour my average speed for this 2 nd hour is halved to 40 km per hour. The average speed for the journey is 60 km per hour.

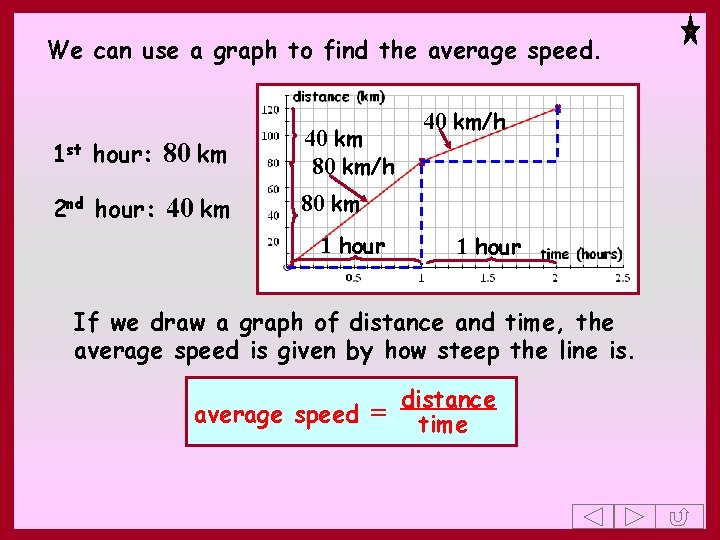
We can use a graph to find the average speed. 1 st hour: 80 km 2 nd hour: 40 km 80 km/h 40 km/h 80 km 1 hour If we draw a graph of distance and time, the average speed is given by how steep the line is. distance average speed = time

distance average speed = time We can use this formula to find either: speed if we know distance and time, or distance if we know speed and time, or time if we know distance and speed. Tip: A way to remember this formula: • Write d, s, and t in alphabetical order in a “warning” triangle. d s t

distance average speed = time We can use this formula to find either: speed if we know distance and time, or distance if we know speed and time, or time if we know distance and speed. Tip: A way to remember this formula: • Write d, s, and t in alphabetical order in a “warning” triangle. d s t Tip: Check the letters are in the right order by noting the units for speed. e. g. km/h, kilometres over hours.

distance average speed = time We can use this formula to find either: speed if we know distance and time, or distance if we know speed and time, or time if we know distance and speed. Tip: A way to remember this formula: • Write d, s, and t in alphabetical order in a “warning” triangle. d s t For distance time cover speed cover upupthe up thethe t. s. d. The triangle givesover d over t speed isdistance over time is speed. distance is speed time (distance over time).

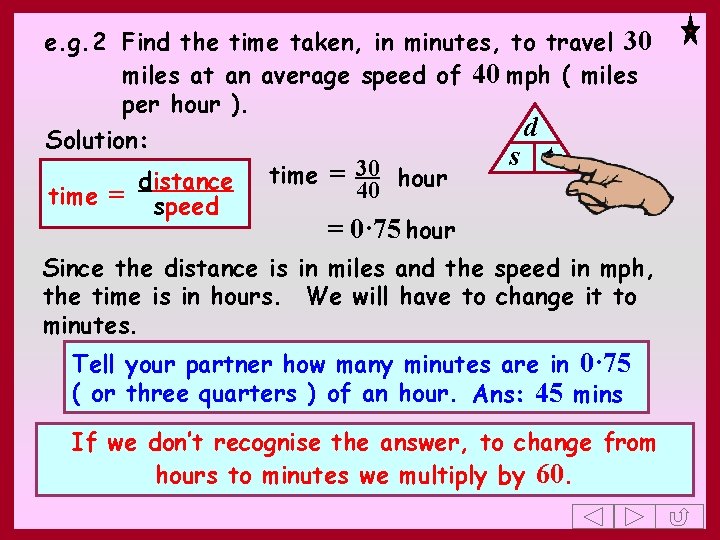
e. g. 2 Find the time taken, in minutes, to travel 30 miles at an average speed of 40 mph ( miles per hour ). d Solution: s t 30 distance time = 40 hour time = speed = 0· 75 hour Since the distance is in miles and the speed in mph, the time is in hours. We will have to change it to minutes. Tell your partner how many minutes are in 0· 75 ( or three quarters ) of an hour. Ans: 45 mins If we don’t recognise the answer, to change from hours to minutes we multiply by 60.

e. g. 3 Without using a calculator, find the distance travelled on a trip that takes 20 minutes if the average speed is 6 km/h. Solution: Without a calculator, if we have mixed units. . .

e. g. 3 Without using a calculator, find the distance travelled on a trip that takes 20 minutes if the average speed is 6 km/h. Solution: Without a calculator, if we have mixed units. . . it is often easier not to use the formula. A speed of 6 km/h means 6 km travelled in 1 hour ( or 60 minutes ). This is 1 km in 10 minutes or 2 km in 20 minutes. The answer is 2 km.

SUMMARY Ø We can use a warning triangle to find the formula that links average speed, distance and time. d s t letters in alphabetical order, distance average speed = time distance time = speed distance = speed time Ø If the units for speed are km/h, the units for distance must be km and for time must be hours. Ø Non-calculator problems are usually easier without the formula.

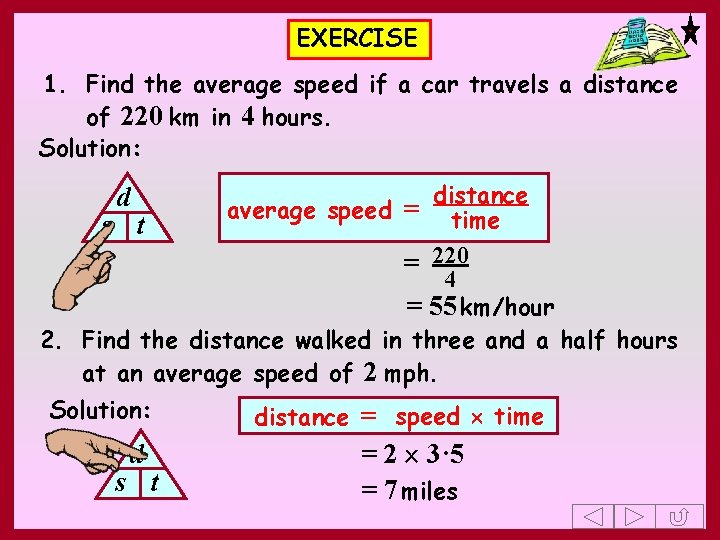
EXERCISE 1. Find the average speed if a car travels a distance of 220 km in 4 hours. 2. Find the distance walked in three and a half hours at an average speed of 2 mph. 3. Find the time taken to run 5 km at an average speed of 8 km/h. Give your answer in minutes. 4. Without using a calculator, find the average speed for a journey of 10 miles in 15 minutes. Give your answer in miles per hour.

EXERCISE 1. Find the average speed if a car travels a distance of 220 km in 4 hours. Solution: distance average speed = time s t = 220 4 = 55 km/hour 2. Find the distance walked in three and a half hours at an average speed of 2 mph. d Solution: d s t distance = speed time = 2 3· 5 = 7 miles

EXERCISE 3. Find the time taken to run 5 km at an average speed of 8 km/h. Give your answer in minutes. Solution: d s t distance time = speed = 5 8 = 0· 625 hours = 0· 625 60 minutes = 37· 5 minutes

EXERCISE 4. Without using a calculator, find the average speed for a journey of 10 miles in 15 minutes. Give your answer in miles per hour. Solution: We need to find the distance travelled in 1 hour ( 60 minutes ). We have the distance travelled in 15 minutes. 10 miles in 15 minutes Doubling the numbers: 20 miles in 30 minutes Doubling again: 40 miles in 60 minutes The average speed is 40 mph.