Teach A Level Maths Statistics 1 The Central

The Central Limit Theorem S 1: The Central Limit Theorem AQA Normal Distribution diagrams

The Central Limit Theorem How Good are Estimates? In the previous presentation we met

The Central Limit Theorem Population and 1000 sample means Population: Samples: n=5 mean Population

The Central Limit Theorem Population and 1000 sample means n=5 Population and 1000 sample

The Central Limit Theorem The standard deviation of the distribution of the sample means

The Central Limit Theorem We now know the following facts about the distribution of

The Central Limit Theorem e. g. 1. A General Studies test was given to

The Central Limit Theorem Part (c) of the last question illustrates a useful principle.

The Central Limit Theorem e. g. 2. The heights of plants grown from a

The Central Limit Theorem Exercise 1. The length of telephone calls received by an

Exercise 2. The Central Limit Theorem A Normal distribution has a mean of 40

The Central Limit Theorem 2. A Normal distribution has a mean of 40 and

The Central Limit Theorem Exercise 3. The random variable X has a distribution (a)

The Central Limit Theorem The following slides contain repeats of information on earlier slides,

The Central Limit Theorem (c) This part illustrates a useful principle. We halved the

Slides: 26

Download presentation

“Teach A Level Maths” Statistics 1 The Central Limit Theorem © Christine Crisp

The Central Limit Theorem S 1: The Central Limit Theorem AQA Normal Distribution diagrams in this presentation have been drawn using FX Draw ( available from Efofex at www. efofex. com ) "Certain images and/or photos on this presentation are the copyrighted property of Jupiter. Images and are being used with permission under license. These images and/or photos may not be copied or downloaded without permission from Jupiter. Images"

The Central Limit Theorem How Good are Estimates? In the previous presentation we met a question where the sample was small. So, we couldn’t be sure that the estimate of the population mean was a good one. A numerical measure of the accuracy of an estimate can be made if we know the standard deviation of the population. To explain this, we’ll look again at the diagrams showing the means of 1000 samples from a population of weights of hens’ eggs.

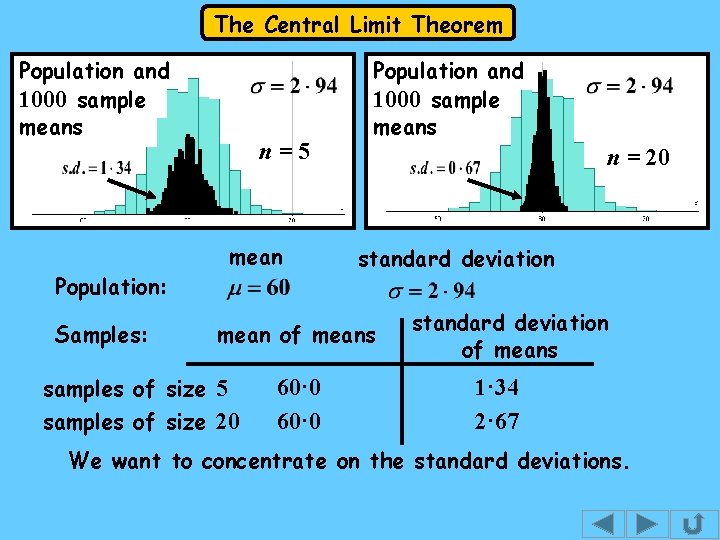
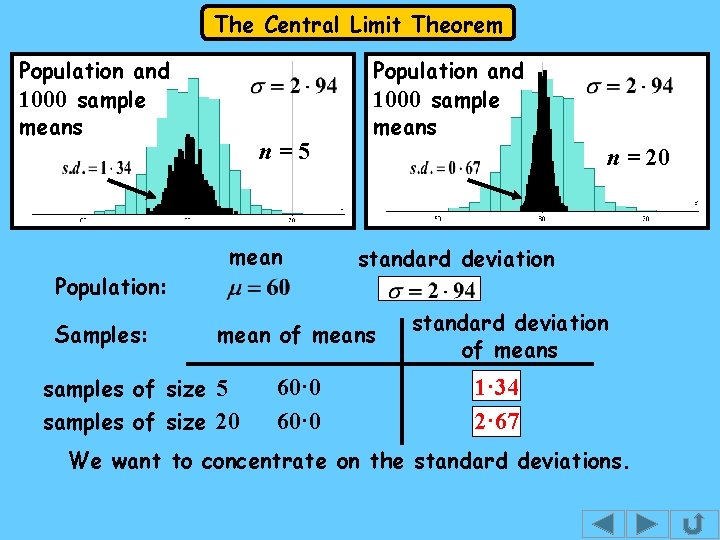
The Central Limit Theorem Population and 1000 sample means Population: Samples: n=5 mean Population and 1000 sample means n = 20 standard deviation mean of means samples of size 5 samples of size 20 60· 0 standard deviation of means 1· 34 2· 67 We want to concentrate on the standard deviations.

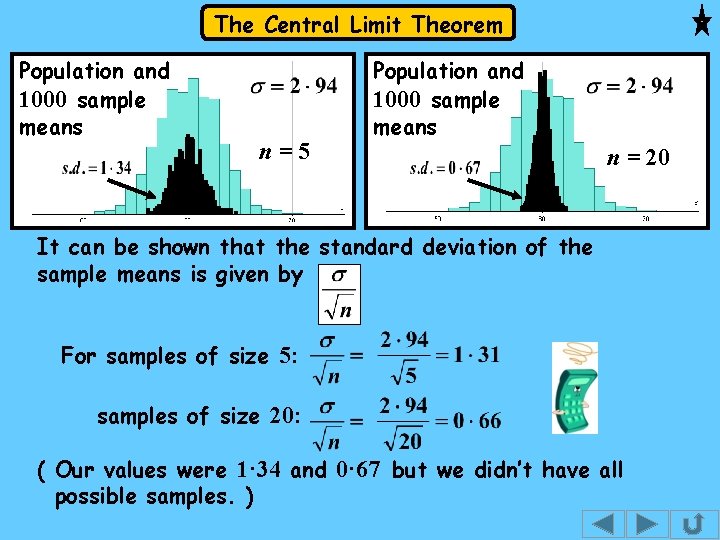
The Central Limit Theorem Population and 1000 sample means n=5 Population and 1000 sample means n = 20 It can be shown that the standard deviation of the sample means is given by For samples of size 5: samples of size 20: ( Our values were 1· 34 and 0· 67 but we didn’t have all possible samples. )

The Central Limit Theorem The standard deviation of the distribution of the sample means is called the standard error of the sample mean, often shortened to the standard error (s. e. ). The standard error is given by where, s is the population standard deviation and n is the size of each sample. Since the distribution of sample means is Normal, approximately 68% of the sample means lie within of the population mean and 95% within ± 2 s. e.

The Central Limit Theorem We now know the following facts about the distribution of the means of samples of size n from a population with an approximately Normal distribution: Ø The distribution of means is approximately Normal. Ø The mean of the means is equal to the population mean, m. Ø The standard deviation is called the standard error and is equal to the population standard deviation, s, divided by. We write Very importantly, the above also hold when the population is not Normal but in this case n should be greater than 30. This is the Central Limit Theorem (C. L. T. )

The Central Limit Theorem e. g. 1. A General Studies test was given to 720 students in a College. The standard deviation of the marks is 20. The following marks are from a random sample of 12 students: 35, 23, 17, 38, 20, 25, 29, 32, 28, 31, 33, 24 (a) Estimate the mean mark of all the students. (b) Find the standard error of your estimate. (c) What size sample would be needed to halve the standard error? The sample Solution: (a) size is less than 30, so we must assume the population is Normal. This is the estimate of m. (b) The standard error = (c)

The Central Limit Theorem Part (c) of the last question illustrates a useful principle. We halved the standard error from 5· 77 to 2· 89 by increasing the sample size from 12 to 48. To halve the standard error we must multiply the sample size by 4. Can you say directly what the sample size would need to be if we wanted the standard error to be a third of its original value? ANS: We need The rule is: To divide s. e. by 2, multiply sample size by To divide s. e. by 3, multiply sample size by The reason is that the formula for the s. e. contains division by. etc.

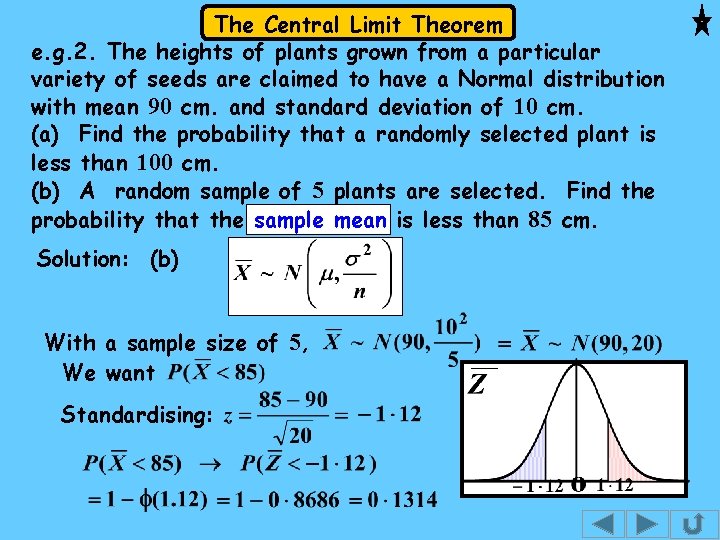
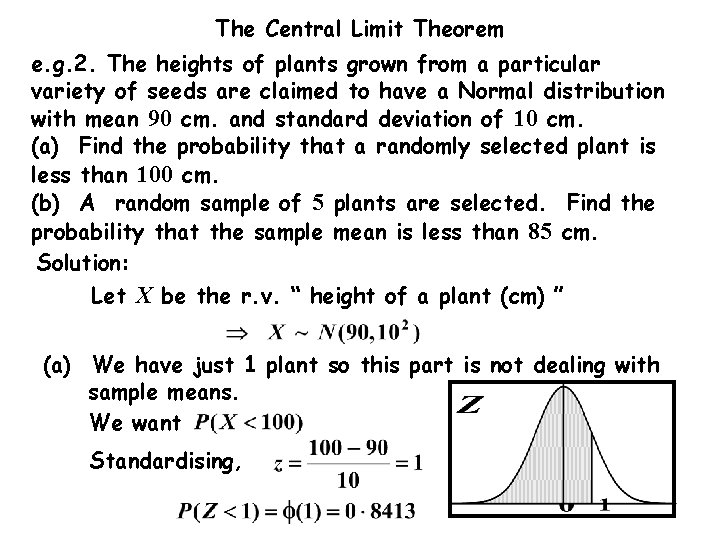
The Central Limit Theorem e. g. 2. The heights of plants grown from a particular variety of seeds are claimed to have a Normal distribution with mean 90 cm. and standard deviation of 10 cm. (a) Find the probability that a randomly selected plant is less than 100 cm. (b) A random sample of 5 plants are selected. Find the probability that the sample mean is less than 85 cm. Solution: Let X be the r. v. “ height of a plant (cm) ” (a) We have just 1 plant so this part is not dealing with sample means. We want N. B. z = 1 because Standardising, 100 is one s. d. above the mean, 90.

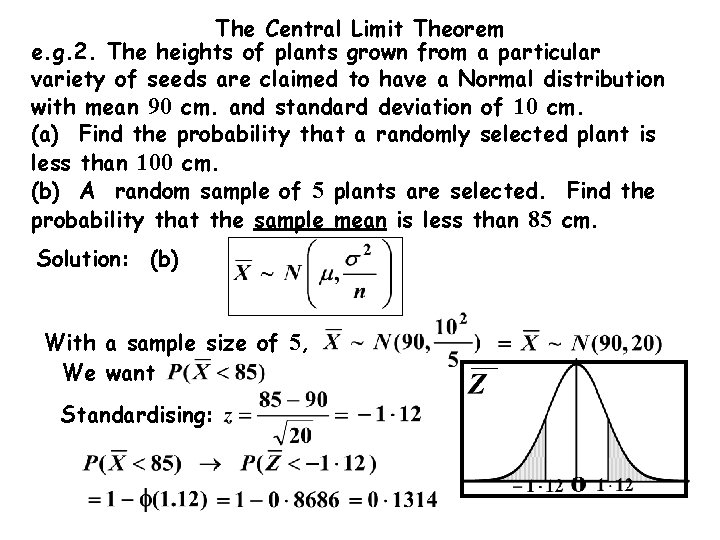
The Central Limit Theorem e. g. 2. The heights of plants grown from a particular variety of seeds are claimed to have a Normal distribution with mean 90 cm. and standard deviation of 10 cm. (a) Find the probability that a randomly selected plant is less than 100 cm. (b) A random sample of 5 plants are selected. Find the probability that the sample mean is less than 85 cm. Solution: (b) With a sample size of 5, We want Standardising:

The Central Limit Theorem Exercise 1. The length of telephone calls received by an organization is known to have a standard deviation of 13 mins. The table gives the lengths of 50 randomly selected telephone calls. Length (min) 1 -2 3 -5 6 -8 9 -11 Frequency 14 12 10 8 12 -17 18 -25 4 2 (a) Use the sample to calculate an estimate of m, the mean length of calls. (b) Find the standard error of your estimate. Solution: N. B. The(a)sample size is (b) greater than 30. The Central Limit Theorem (C. L. T. ) tells us we need not assume the population is Normal.

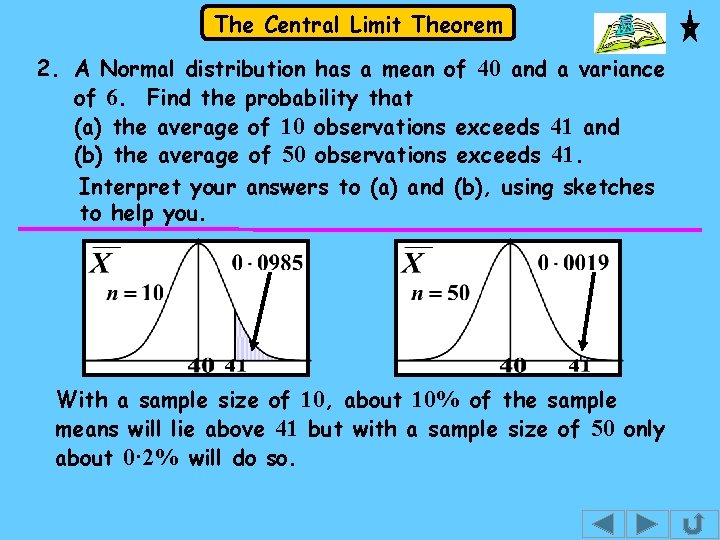
Exercise 2. The Central Limit Theorem A Normal distribution has a mean of 40 and a variance of 6. Find the probability that (a) the average of 10 observations exceeds 41 and (b) the average of 50 observations exceeds 41. Interpret your answers to (a) and (b), using sketches to help you. 3. The random variable X has a distribution (a) Write down the distribution of , the mean of random samples of size 9 taken from X. (b) Find the probability that is less than 45. .

The Central Limit Theorem 2. A Normal distribution has a mean of 40 and a variance of 6. Find the probability that (a) the average of 10 observations exceeds 41 and (b) the average of 50 observations exceeds 41. Interpret your answers to (a) and (b), using sketches to help you. Solution: Let X be the r. v. Then, (a) We want (b) Method as (a) with Ans:

The Central Limit Theorem 2. A Normal distribution has a mean of 40 and a variance of 6. Find the probability that (a) the average of 10 observations exceeds 41 and (b) the average of 50 observations exceeds 41. Interpret your answers to (a) and (b), using sketches to help you. With a sample size of 10, about 10% of the sample means will lie above 41 but with a sample size of 50 only about 0· 2% will do so.

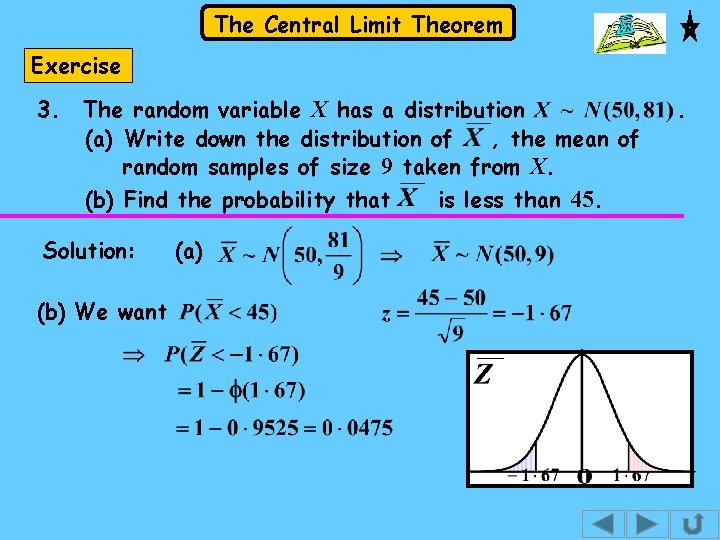
The Central Limit Theorem Exercise 3. The random variable X has a distribution (a) Write down the distribution of , the mean of random samples of size 9 taken from X. (b) Find the probability that is less than 45. Solution: (b) We want (a) .

The Central Limit Theorem The following slides contain repeats of information on earlier slides, shown without colour, so that they can be printed and photocopied. For most purposes the slides can be printed as “Handouts” with up to 6 slides per sheet.

The Central Limit Theorem e. g. 1. A general studies test was given to 720 students in a College. The standard deviation of the marks is 20. The following marks are from a random sample of 12 students: 35, 23, 17, 38, 20, 25, 29, 32, 28, 31, 33, 24 (a) Estimate the mean mark of all the students. (b) Find the standard error of your estimate. (c) What size sample would be needed to halve the standard error? The sample size is less than 30, so we must assume the population is Normal. Solution: (a) This is the estimate of m. (b) The standard error =

The Central Limit Theorem (c) This part illustrates a useful principle. We halved the standard error from 5· 77 to 2· 89 by increasing the sample size from 12 to 48. To halve the standard error we must multiply the sample size by 4. To divide the standard error by 3, we need a sample size that is 9 times as large. i. e. 108 The rule is: To divide s. e. by 2, multiply sample size by To divide s. e. by 3, multiply sample size by The reason is that the formula for the s. e. contains division by. etc.

The Central Limit Theorem e. g. 2. The heights of plants grown from a particular variety of seeds are claimed to have a Normal distribution with mean 90 cm. and standard deviation of 10 cm. (a) Find the probability that a randomly selected plant is less than 100 cm. (b) A random sample of 5 plants are selected. Find the probability that the sample mean is less than 85 cm. Solution: (b) With a sample size of 5, We want Standardising: