Teach A Level Maths Statistics 1 Confidence Intervals

“Teach A Level Maths” Statistics 1 Confidence Intervals © Christine Crisp

Confidence Intervals Statistics 1 AQA Normal Distribution diagrams in this presentation have been drawn using FX Draw ( available from Efofex at www. efofex. com ) "Certain images and/or photos on this presentation are the copyrighted property of Jupiter. Images and are being used with permission under license. These images and/or photos may not be copied or downloaded without permission from Jupiter. Images"

Confidence Intervals We know that the best estimate of a population mean is the mean of a random sample. The larger the sample size, the better the estimate. We also saw that the standard error of the distribution of sample means gives a measure of the accuracy of the estimate and that poor estimates occur rarely. All of these comments are vague, so the final thing we want to do is give some numerical indication of accuracy. We do this by • giving an interval of values within which the population mean is likely to lie and • saying how likely it is that the interval contains the mean.

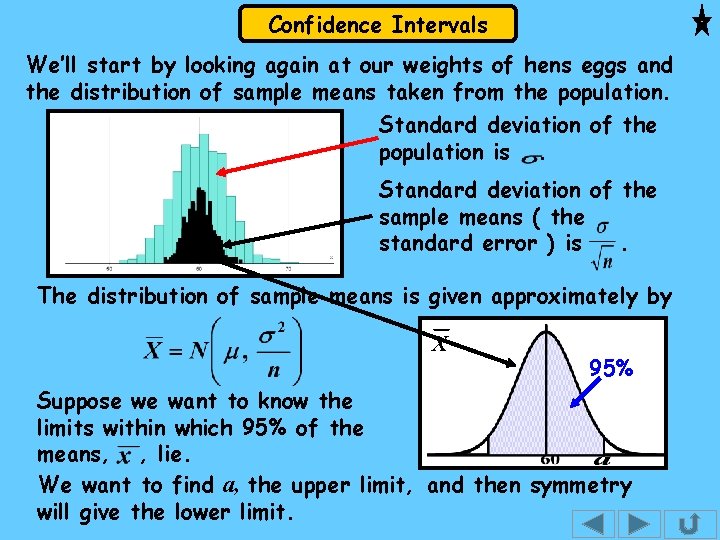
Confidence Intervals We’ll start by looking again at our weights of hens eggs and the distribution of sample means taken from the population. Standard deviation of the population is. Standard deviation of the sample means ( the standard error ) is. The distribution of sample means is given approximately by X 95% Suppose we want to know the limits within which 95% of the means, , lie. We want to find a, the upper limit, and then symmetry will give the lower limit.

Confidence Intervals X 95% Using the table “Percentage points of the Normal Distribution”, we can find the z value Z ( Remember the table uses so we needed 0· 975 not 0· 95 ) 97. 5% z

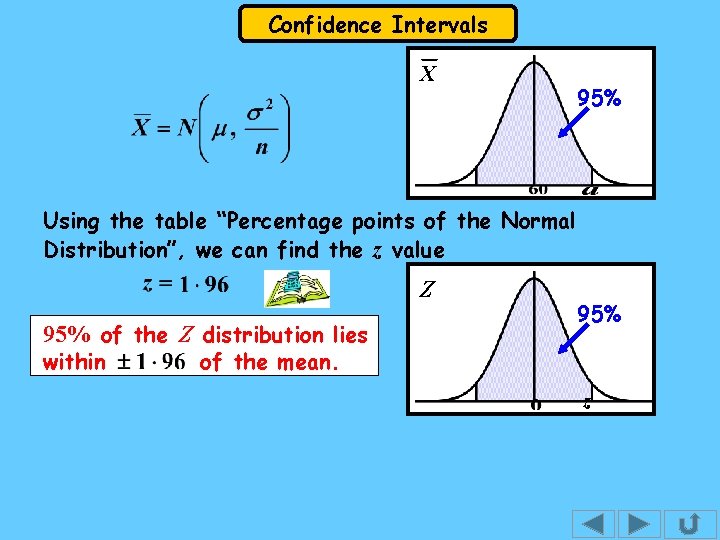
Confidence Intervals X 95% Using the table “Percentage points of the Normal Distribution”, we can find the z value Z 95% of the Z distribution lies within 95% of the mean. z

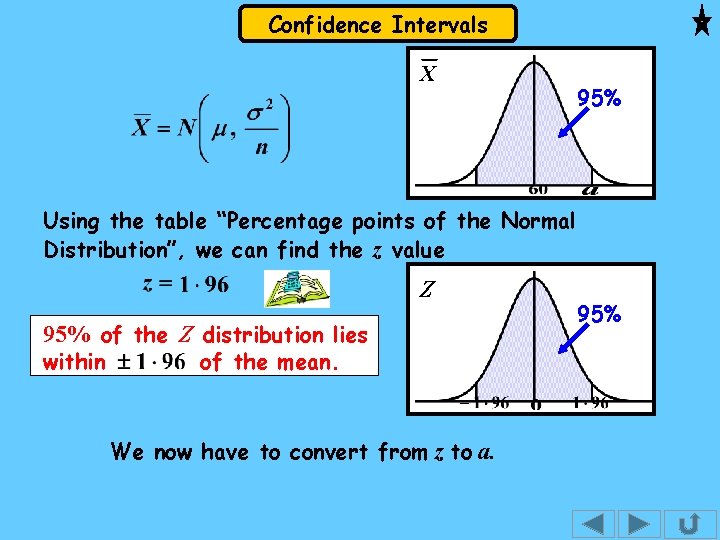
Confidence Intervals X 95% Using the table “Percentage points of the Normal Distribution”, we can find the z value Z 95% of the Z distribution lies within of the mean. We now have to convert from z to a. 95%

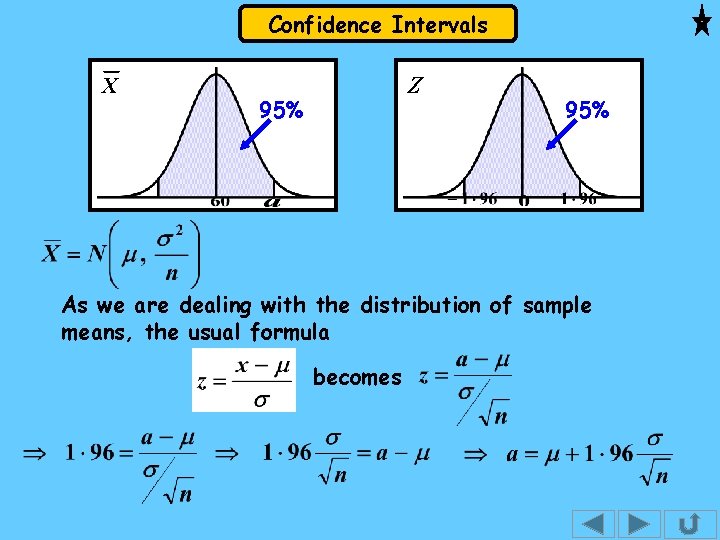
Confidence Intervals X Z 95% As we are dealing with the distribution of sample means, the usual formula becomes

Confidence Intervals X 95% So, 95% of the sample means, ( the within the interval distribution ) lie This inequality gives an interval within which lies. However, we want to know how good our estimate of m is, so we need an interval for m. We just need to rearrange.

Confidence Intervals Dealing with the 2 parts separately: and Now putting them together again:

Confidence Intervals Dealing with the 2 parts separately: and Now putting them together again:

Confidence Intervals Dealing with the 2 parts separately: and Now putting them together again:

Confidence Intervals Dealing with the 2 parts separately: and Now putting them together again: Since the inequality expresses an interval, we often write

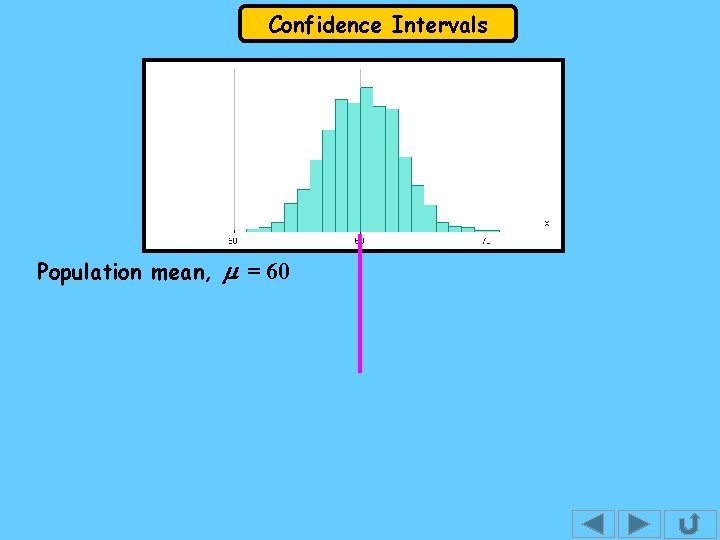
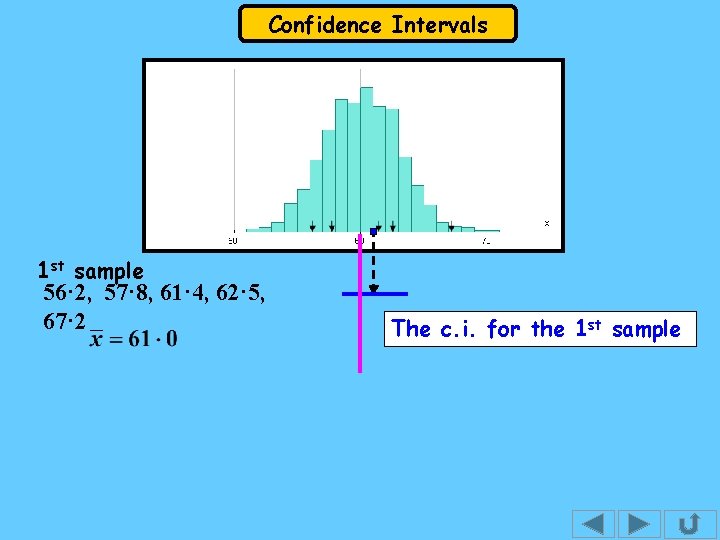
Confidence Intervals The interval is called the 95% confidence interval for the estimate of the population mean using a sample mean of size n. The percentage of confidence tells us that if we had 100 samples each of size n and we formed an interval for each, we would expect 95 of the intervals to contain the population mean. The hens eggs data had a mean of 60 and a standard deviation of, s = 2· 94. Suppose we take a sample of size 5 and it has mean, = 61· 0, the interval is

Confidence Intervals The 95% confidence interval (c. i. ) is This statement says that there is a probability of 0· 95 that the interval from 58· 4 to 63· 6 contains m. So, we expect a similar statement to be true 95 times out of a 100 ( and wrong 5 times out of 100 ! ). The diagram that follows shows this c. i. and those for several other samples of size 5 from the hens eggs data.

Confidence Intervals Population mean, m = 60

Confidence Intervals 1 st sample 56· 2, 57· 8, 61· 4, 62· 5, 67· 2 The c. i. for the 1 st sample

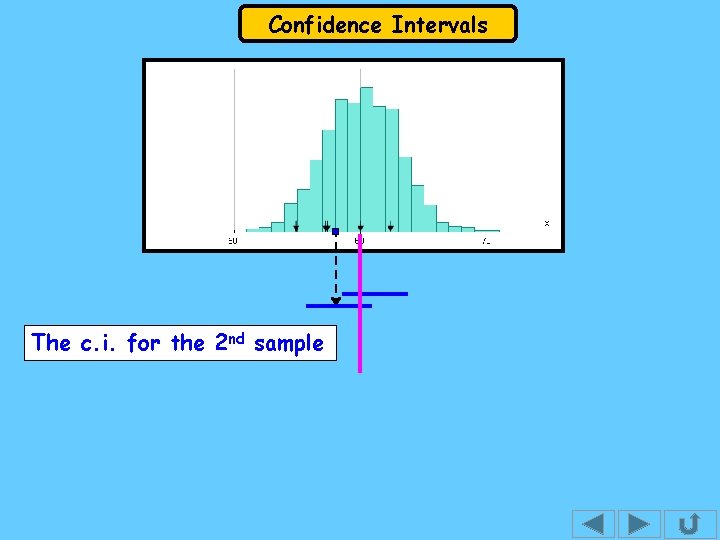
Confidence Intervals The c. i. for the 2 nd sample

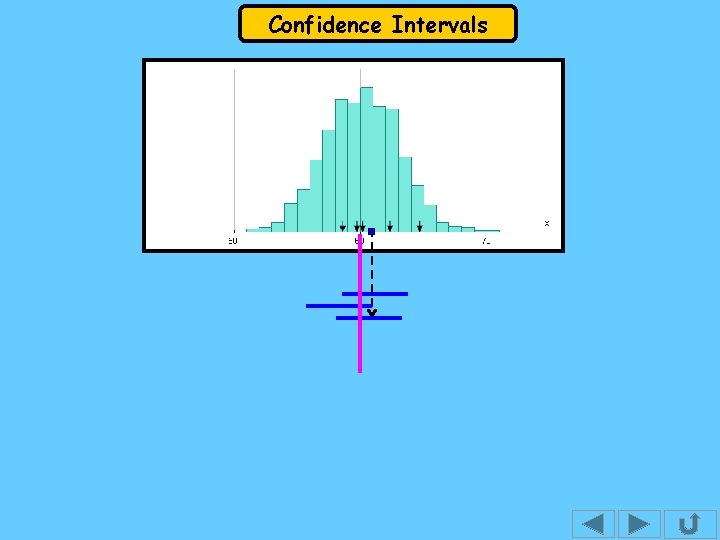
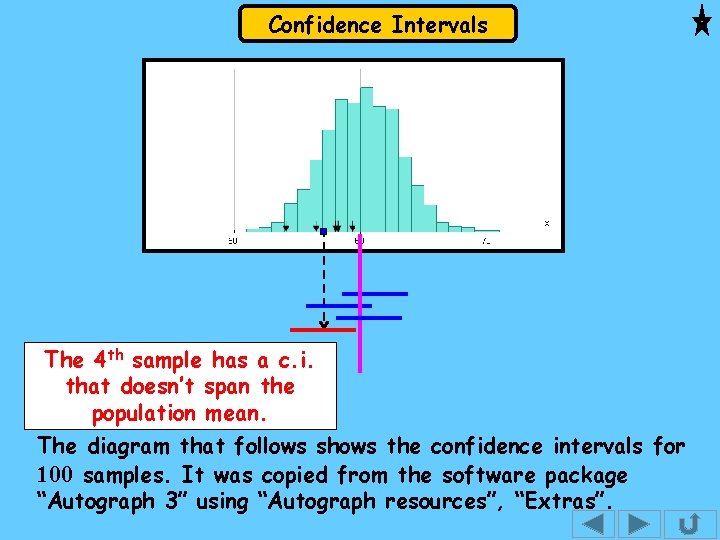
Confidence Intervals

Confidence Intervals The 4 th sample has a c. i. that doesn’t span the population mean. The diagram that follows shows the confidence intervals for 100 samples. It was copied from the software package “Autograph 3” using “Autograph resources”, “Extras”.

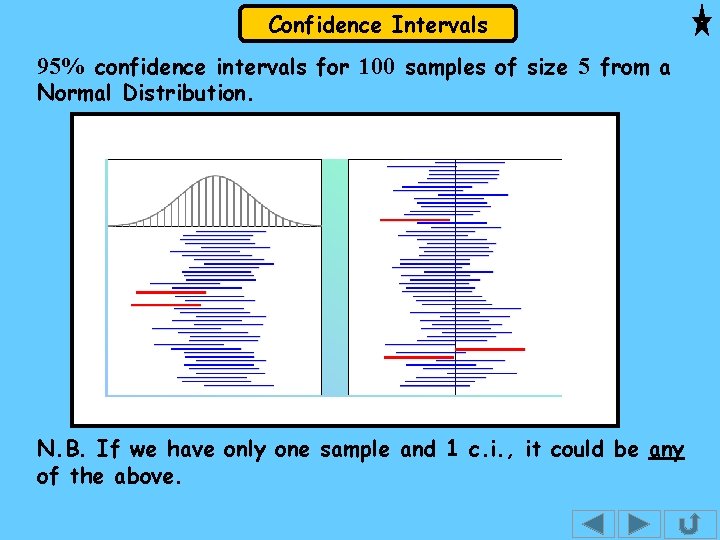
Confidence Intervals 95% confidence intervals for 100 samples of size 5 from a Normal Distribution. N. B. If we have only one sample and 1 c. i. , it could be any of the above.

Confidence Intervals When I took another 100 samples, again of size 5 and I again drew the 95% confidence intervals, I got the following: Why are there only 4 intervals that don’t include m ? ANS: As we are dealing with samples, whilst on average we will get 5, we could, with any one set of 100 samples, get more or less than 5.

Confidence Intervals SUMMARY Ø The 95% confidence interval (c. i. ) for an estimate of the population mean is where, • is the sample mean and • is the standard deviation of the distribution of sample means, the standard error. • 1· 96 is the “z” value corresponding to the central 95% of a Normal distribution. Ø If the population does not have a Normal distribution, we need

Confidence Intervals The 95% confidence interval (c. i. ) for an estimate of the population mean is Now suppose we can’t accept being wrong 5% of the time and want to be wrong only 1% of the time. Exercise What will happen to the width of the c. i. ? Which part of the formula will change and what will it change to?

Confidence Intervals The 95% confidence interval (c. i. ) for an estimate of the population mean is Now suppose we can’t accept being wrong 5% of the time and want to be wrong only 1% of the time. What will happen to the width of the c. i. ? ANS: It will increase. Which part of the formula will change and what will it change to? ANS: The z value, 1· 96, changes. Using p = 0· 995 in the table: z = 2· 5758 Z 99%

Confidence Intervals e. g. 1(a) Find the 80% confidence interval for the mean of a population with standard deviation 5 using a random sample of size 40 with mean 20. (b) In (a) did we need to assume the population has a Normal distribution? Solution: (a) The formula for a c. i. for m is Standard error: Find the z value: the 80% c. i. for m is Z 90% 80%

Confidence Intervals e. g. 1(a) Find the 80% confidence interval for the mean of a population with standard deviation 5 using a random sample of size 40 with mean 20. (b) In (a) did we need to assume the population has a Normal distribution? Solution: (b) No. The Central Limit Theorem says that with a large sample, the population need not be Normal.

Confidence Intervals e. g. 2. Find the width of the 95% c. i. for the population mean of a variable with variance 16 using a random sample of size 40. Solution: The formula for the 95% c. i. for m is so, the width is ( which doesn’t depend on )

Confidence Intervals Exercise 1. Calculate the 95% confidence interval for each of the following samples taken from a Normal distribution: (a) (b) 2. Write down the width of the intervals found in 1(a) and (b). By what factor did the width of the c. i. change from (a) to (b) and why did it change by this amount? 3. What is the formula for a 90% c. i. for a population mean?

Confidence Intervals Solutions: 1. Formula for 95% confidence interval for m is (a) C. i. is (b) C. i. is

Confidence Intervals 2. Write down the width of the intervals found in 1(a) and (b). By what factor did the width of the c. i. change from (a) to (b) and why did it change by this amount? Solution: The intervals were: (a) , n=5 (b) , n = 20 Widths: (a) 5· 2 (b) 2· 6 Width is halved. In (b) the sample size, n, was 4 times larger than in (a) but, in finding the c. i. , we divide by so the result is divided by ( = 2 ).

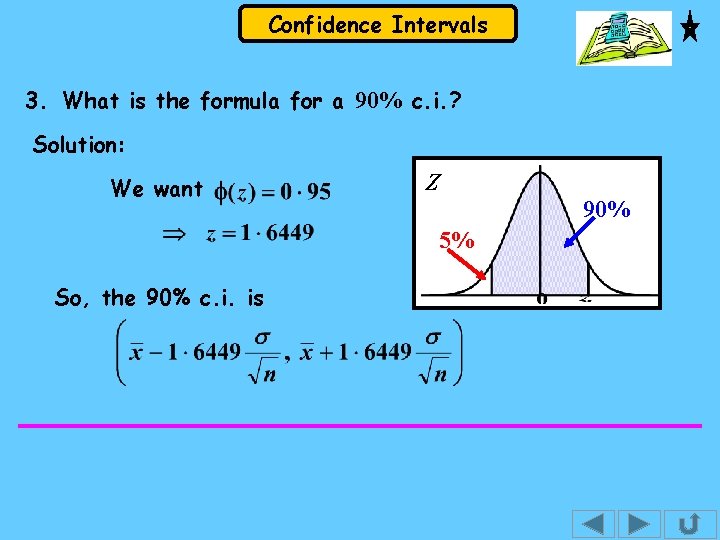
Confidence Intervals 3. What is the formula for a 90% c. i. ? Solution: We want Z 5% So, the 90% c. i. is 90%

Confidence Intervals SUMMARY Ø Formulae for some of the confidence intervals are: 90% : 95% : 99% : Ø Apart from the z value for the 95% interval, which you may want to remember, use a sketch and look up the z value in the table. Remember the percentage for the c. i. is the middle area and the table uses the left-hand area ( e. g. the 90% c. i. uses 0· 95 ). continued:

Confidence Intervals SUMMARY Ø Increasing the sample size by a factor of 4, divides the previously calculated standard error by 2, so halves the width of the confidence interval. e. g. 95% c. i. , Ø Taking large samples can be very expensive, so, in practice, to reduce the width of the c. i. , we may need to reduce the level of confidence instead of increasing the sample size.

Confidence Intervals Unknown Population Standard Deviation It is quite likely that we won’t know the standard deviation of the population. In this case, we must estimate it from the sample. We use the unbiased estimator:

Confidence Intervals e. g. Find the 90% c. i. for the population mean using the following random sample from a variable with a Normal distribution: 3, 6, 10, 14, 17 Solution: Using calculator functions: sample values unbiased estimator s 90% c. i. is

Confidence Intervals Exercise 1. Potatoes are sold in bags marked “ 5 kg”. The weights can be assumed to be normally distributed. A random sample of 10 bags were weighed ( weights in kg. ) and found to be as follows: 5· 04, 5· 21, 5· 11, 4· 82, 5· 32, 5· 41, 4· 82, 4· 89, 5· 22, 5· 23 (a) Calculate a 95% confidence interval for the population mean weight giving the limits to two decimal places. (b) Use the sample and the confidence interval to comment on the claim that the bags weigh 5 kg.

Confidence Intervals Solution: (a) 95% c. i. is given by 5· 04, 5· 21, 5· 11, 4· 82, 5· 32, 5· 41, 4· 82, 4· 89, 5· 22, 5· 23 Sample mean: Unbiased estimator of population standard deviation: Standard error = 95% c. i. : (b) Although only 3 values in the sample are less than 5 kg, and the sample mean is greater than 5 kg, the c. i. shows that the mean weight of the bags could be less than 5 kg.

Confidence Intervals The following slides contain repeats of information on earlier slides, shown without colour, so that they can be printed and photocopied. For most purposes the slides can be printed as “Handouts” with up to 6 slides per sheet.

Confidence Intervals We know that the best estimate of a population mean is the mean of a random sample. The larger the sample size, the better the estimate. We also saw that the standard error of the distribution of sample means gives a measure of the accuracy of the estimate and that poor estimates occur rarely. All of these comments are vague, so the final thing we want to do is give some numerical indication of accuracy. We do this by • giving an interval of values within which the population mean is likely to lie and • we say how likely it is that the mean is within the interval.

Confidence Intervals The interval is called the 95% confidence interval for the estimate of the population mean using a sample mean of size n. The percentage of confidence tells us that if we had 100 samples each of size n and we formed an interval for each, we would expect 95 of the intervals to contain the population mean. The hens eggs data had a mean of 60 and a standard deviation of, s = 2· 94. Suppose we take a sample of size 5 and it has mean, = 61· 0, the interval is

Confidence Intervals The 95% confidence interval (c. i. ) is This statement says that there is a probability of 0· 95 that the interval from 58· 4 to 63· 6 contains m. So, we expect a similar statement to be true 95 times out of a 100 ( and wrong 5 times out of 100 ! ). The diagram that follows shows this c. i. and those for several other samples of size 5 from the hens eggs data.

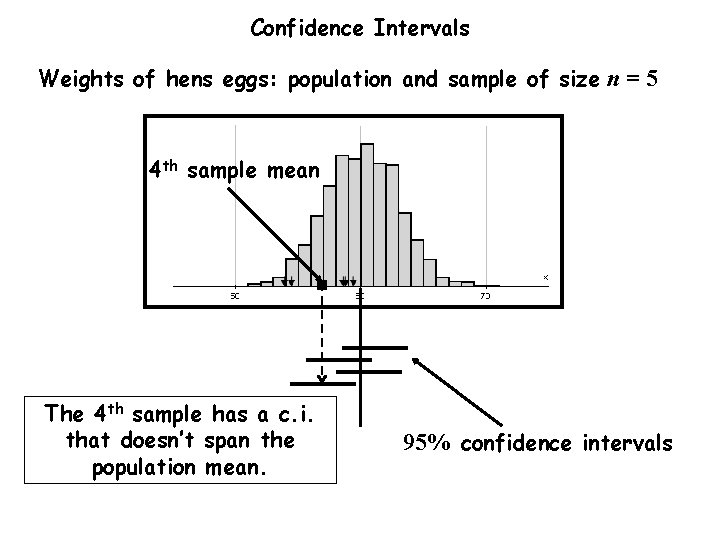
Confidence Intervals Weights of hens eggs: population and sample of size n = 5 4 th sample mean The 4 th sample has a c. i. that doesn’t span the population mean. 95% confidence intervals

Confidence Intervals SUMMARY Ø The 95% confidence interval (c. i. ) for an estimate of the population mean is where, • is the sample mean and • is the standard deviation of the distribution of sample means, the standard error. • 1· 96 is the “z” value corresponding to the central 95% of a Normal distribution. Ø If the population does not have a Normal distribution, we need n > 30.

Confidence Intervals The 95% confidence interval (c. i. ) for an estimate of the population mean is Now suppose we can’t accept being wrong 5% of the time and want to be wrong only 1% of the time. The z value, 1· 96, must change. Instead of the z value that gives the central 95% of the distribution we want 99%. So, we need the area to the left of z to equal 99· 5%. Using p = 0· 995 in the table: z = 2· 5758 Z 99%

Confidence Intervals SUMMARY Ø Formulae for some of the confidence intervals are: 90% : 95% : 99% : Ø Apart from the z value for the 95% interval, which you may want to remember, use a sketch and look up the z value in the table. Remember the percentage for the c. i. is the middle area and the table uses the left-hand area ( e. g. the 90% c. i. uses 0· 95 ). continued:

Confidence Intervals Ø Increasing the sample size by a factor of 4, divides the standard error by 2, so halves the width of the confidence interval. e. g. 95% c. i. , Ø Taking large samples can be very expensive, so, in practice, to reduce the width of the c. i. , we may need to reduce the level of confidence instead of increasing the sample size.

Confidence Intervals Unknown Population Standard Deviation It is quite likely that we won’t know the standard deviation of the population. In this case, we must estimate it from the sample. We use the unbiased estimator:

Confidence Intervals e. g. Find the 90% c. i. for the population mean using the following random sample from a variable with a Normal distribution: 3, 6, 10, 14, 17 Solution: Using calculator functions: sample values unbiased estimator s 90% c. i. is